题解 P2151 【[SDOI2009]HH去散步】
LeavingZzz
·
·
题解
P2151 题解
by LeavingZ
upd on 2023.9.2 增加了对 t=0 的特判并且修改了快速幂的写法使其能处理指数为 0 的情况。
在一切开始之前
请确保题目您已经仔细看完了。
蒟蒻也是刚学矩阵加速,做到了这道题,做了很久才做出来,希望分享自己的思维历程给大家。
一点闲话(若只是想看该题解法请跳过)
这道题要求的是图中定长路线的方案数,这种题目是可以将邻接矩阵进行乘幂的,如果您不知道这个,您可以先去做一下这道题
但是很多人(包括我)不理解邻接矩阵乘幂到底有什么意义,或者他是怎么来的,我在这里和大家简单的说(bian)一下[始终要注意邻接矩阵是一个方阵]。
看下面这个图:
这里以矩阵的 2 次幂为例,按刚才的说法就是长度为 2 的线路的方案数。
比如原矩阵的 (1,2) 表示点 1 可以到点 2 去,而矩阵乘法可以看做是图中的两个箭头不断地走,比如黑箭头在走第一行的时候,第二个元素是 1,要想新矩阵中有含 1 的元素,右边蓝箭头走到第 2 个元素时也得出现 1 才可以
而我们知道,右边蓝箭头走到第二个元素就是第二行,也就是从点 2 出发可以到达的点,当点 1 可以到点 2 时,从点 2 出发的可以到达的所有点与点 1 的距离都是 2,符合我们说的矩阵2次幂的意义。
main()
那么这道题要干什么呢,也是求路径方案数,也是定长,但是有个限制让它变得不是那么裸,就是它是无向图但是不可以直接沿着一条边走过来马上走回去,那么我们怎么办呢?
在抛开一切的情况下我们想一下,如果没有限制,我们会用 DP 的做法,以已经走过来的距离划分阶段,F[i][j] 表示走过 i 距离的时候在 j 点的方案数那么有:
F[i][j]=\sum\limits_{k\in to[j]} F[i-1][k]
那么如果我们再用这种状态的定义和转移来看看这道题呢,那你很快就会发现解决不了,因为这样的话由于是无向边,转移很有可能就违背了约束(刚刚转移到这个点马上转移回去),那么我们就会用到常用的一个技巧就是**点边互换**。
将点边互换,上述转移方程**几乎不变**:
$$F[i][j]=\sum\limits_{k\in to[j]} F[i-1][k]$$
$to[j]$ 表示能够到达 $j$ 边的边集
能够到达 $j$ 边的边集就是终点为边j的始点的边组成的集合
(这里都说了始点和终点了难道看不出来是把无向边1拆2吗)
为满足题目条件,只需要在 $to[j]$ 中去除掉j的反边就可以了。
ah♂~,这道题我已经.....不对,距离小于等于 $2e9$ ...(~~MLE反光~~)
那么我们怎么优化呢?
我们的方程是那个样子,,,,这道题又谈到了**定长路线方案数**,考虑用矩阵来优化,把状态存到一个矩阵里面,再**构造一个转移矩阵**来进行转移。
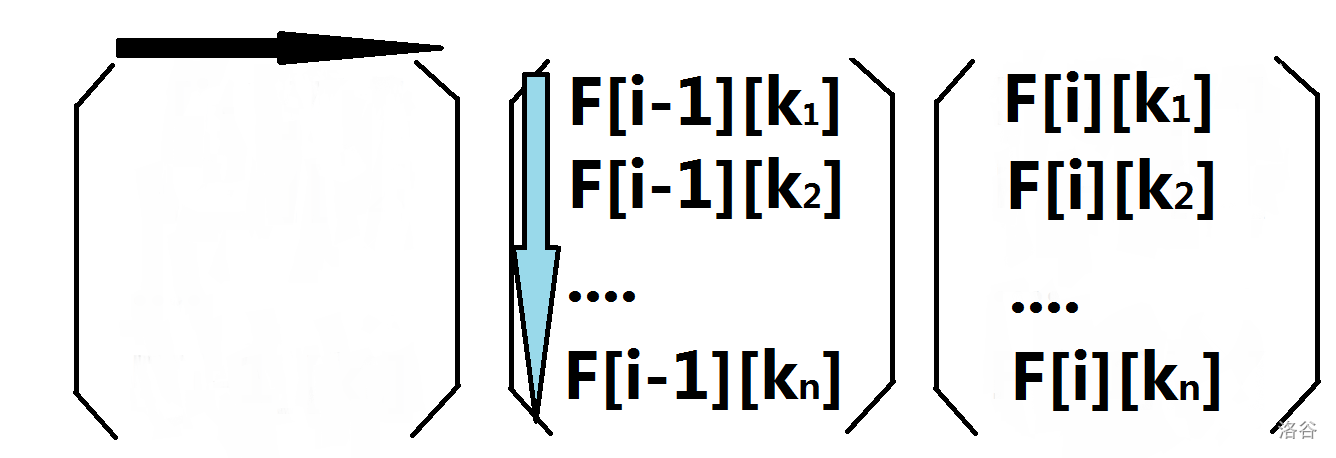
$$F[i][k]=\sum\limits_{j\in to[k]} F[i-1][j]$$
$to[k]$ 表示能够到达 $k$ 边的边集
怎么让这个矩阵体现这这个方程呢?
注意到那两个箭头了吗?
第一个矩阵中第 $x$ 行的第 $y$ 个元素如果是$1$的话那么在最右边的结果矩阵中得到的新状态 $F[i][k_x]$ 就会把第二个矩阵中的 $F[i-1][k_y]$ 累加进去,如果是$0$的话就不会累加。
所以我们为了满足状态转移方程,对于最左边矩阵(即转移矩阵)中的第 $k$ 行只将 $to[k]$ 中的对应元素设为$1$,**也就是说,$m[x][y]=1$ 表示编号为 $y$ 的边可以转移到编号为 $x$ 的边上去**,那么转移矩阵就被构造成了一个边长 $2M$ 的方阵。
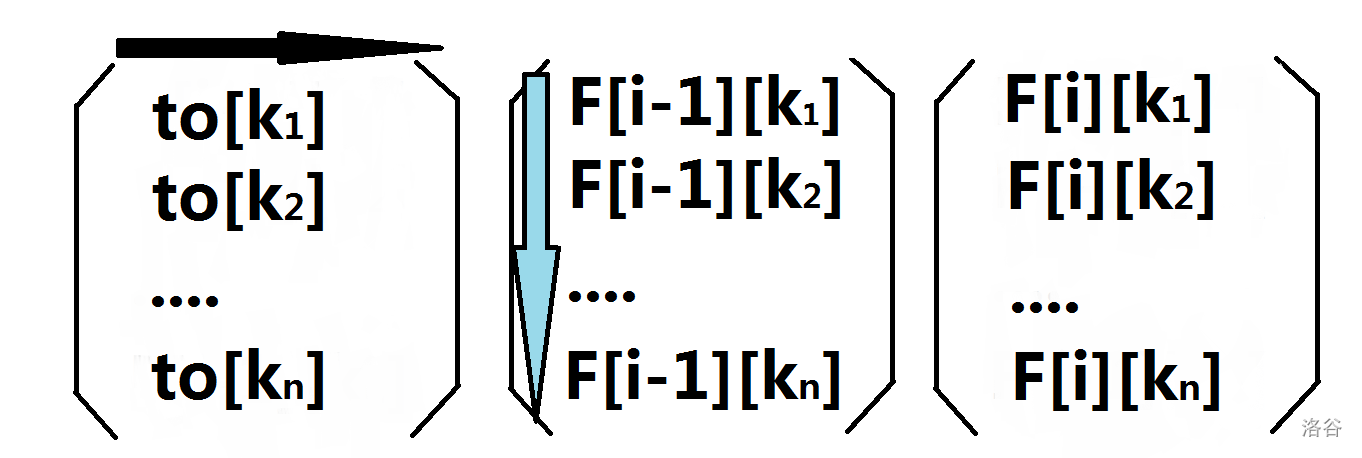
$to[k]$ 表示的是可以转移到第 $k$ 条边的边集,这个地方我们用一行 $01$ 表示不包含与包含,如果第 $x$ 条边可以转移到第 $y$ 条边就把 $m[y][x]$ 置成 $1$,否则为 $0$ (**下标不要搞反了**)
答案状态要从初始状态一步步转移来,那么要转移多少次呢?我们是按照走出的距离划分阶段的,所以要转移$t$次
矩阵乘法满足结合律但是不满足交换律,所以答案状态就是初始矩阵乘以转移矩阵的 $t$ 次幂(**但是在这道题里面要有点小小的变化**),然后在结果矩阵里把终点为给定终点的方案数累加起来即可。
------------
代码实现相信大家看到这里已经有些想法了,**尽量自己想,这样自己才会有真正的收获**,实在debug太久了再来代码里面找我。
```cpp
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int mod=45989;
struct Matr{
int m[150][150];
int R,C;
Matr() {memset(m,0,sizeof(m));}
Matr operator * (const Matr &a) const
{
Matr t;
t.R=R;t.C=a.C;
for(int i=1;i<=R;i++)
for(int j=1;j<=t.C;j++)
for(int k=1;k<=C;k++)
t.m[i][j]=(t.m[i][j]+(m[i][k]*a.m[k][j])%mod)%mod;
return t;
}
}ini,trans;//分别是初始矩阵和转移矩阵
struct E{
int u,v;
}e[127];//为了更方便的枚举边使用邻接表存储边
int first[57],nt[127],ES;
int N,M,S,T,t;
Matr operator ^ (Matr a,int k)//矩阵快速幂
{
Matr s;
s.C=a.C;s.R=a.R;
for(int i=1;i<=a.R;i++)
s.m[i][i]=1;
while(k)
{
if(k&1) s=s*a;
a=a*a;
k>>=1;
}
return s;
}
int anti(int x)//因为我是从1开始存边所以不能异或只能自己写函数了
{
return x%2==0?x-1:x+1;
}
int main()
{
scanf("%d%d%d%d%d",&N,&M,&t,&S,&T);
if(t==0)//特殊判断t=0的情况
{
puts("0");
return 0;
}
int u,v;S++;T++;//题目给的是0开始编号要记得加
for(int i=1;i<=M;i++)
{
scanf("%d%d",&u,&v);u++;v++;//要记得加
e[++ES]=(E){u,v};
nt[ES]=first[u];
first[u]=ES;
e[++ES]=(E){v,u};
nt[ES]=first[v];
first[v]=ES;
}
for(int i=1;i<=ES;i++)
{//如果某一条边的始点与当前这条边的终点重合
//则称当前这条边可以转移到"某一条边"
for(int k=first[e[i].v];k;k=nt[k])
{
if(k!=anti(i))//记得不可以是反边,否则会违背题目要求
trans.m[k][i]++;//下标千万莫写反了,自己要搞清楚
}
}
trans.C=trans.R=ES;//矩阵大小表示
ini.R=ES;ini.C=1;//表示错了乘法无法正确进行
for(int i=first[S];i;i=nt[i])
ini.m[i][1]++;//由于初状态不好确定
//干脆就把初始矩阵当成已经走出的距离为1时的状态
trans=trans^(t-1);
//因为初始矩阵当成了距离为1的状态这里只能t-1次幂
trans=trans*ini;
int ans=0;
for(int i=first[T];i;i=nt[i])
//直接枚举终点为给定点的边不太好枚举
//就枚举始点为给定终点的边然后取反边即可
ans=(ans+trans.m[anti(i)][1])%mod;//我最开始还没取模.....
printf("%d",ans);
return 0;
}
```
矩阵加速的题目这是很经典的一道,先用 $DP$ (递推)写方程再考虑矩阵的构造,仔细想想,总会A的;
基本思路:
- 点边互换
- 构造边集01矩阵
- 去除反边
- 矩阵快速幂加速
本题易错点总结:
- 矩阵乘法本身写错了。
- 表示状态的下标写反了(或者前后下标意义不一致)。
- 矩阵大小行列傻傻分不清QwQ。
- 矩阵乘法不满足交换律,而做乘法的时候写反了。
如果有任何问题或者不明白都可以在讨论中发表您的意见或者直接私信我,我会尽力帮您解决。
谢谢管理大大审核^_^