鸽巢原理及其扩展——Ramsey定理
ShineEternal
2018-08-23 10:11:55
# 第一部分:鸽巢原理
别名:鸽笼原理。狄利克雷抽屉原理。
**最简单的一种形式**:有$m+1$只鸽子,$m$个笼子,那么至少有一个笼子有至少两只鸽子。当然,换个角度来说:有$m-1$只鸽子,$m$个笼子,那么至少有一个笼子是空的。

**初级加强**:有$m$个笼子,$k*m+1$只鸽子,那么至少有一个笼子有至少$k+1$只鸽子。
**高级加强**:令
- $a_1,a_2,a_3...a_m$
- 为正整数。
- $if$ 我们将
- $a_1+a_2+a_3+...+a_n-n+1$
- 个鸽子放入$n$个笼子里,$then$,
||第一个笼子至少有$a_1$只鸽子||第二个笼子至少有$a_2$只鸽子||第三个笼子至少有$a_3$只鸽子||...||第$m$个笼子至少有$a_m$只鸽子
------------
# 鸽巢原理的应用
**一位洛谷$oier$要用$12$周的时间准备$~~CTSC~~$,为了练习,他每天至少要刷一题,因为题目有难度,他每星期刷题无法超过$13$题。请你证明:存在连续的若干天期间,这位$oier$恰好刷了$11$题**
开始证明:
1.我们可以令$a_1$表示第一天所刷的题数,$a_2$表示前两天所刷的题数,$a_3$表示前三天所刷的题数.之后以此类推
2.而题目说,由于每天都要至少刷1题,所以数列
- $a_1,a_2,a_3,a_4,...,a_{84}$
- 严格递增。另有$a_1>=1$.又每周最多刷13题,故$a_{84}<=13*12=156$.
3.因此又有:
- $1<=a_1<a_2<a_3<...<a_{84}<=156$.
4.同理,
- $a_1+11,a_2+11,a_3+11,...,a_{84}+11$
- 同样是一个严格递增序列。范围:
- $12<=a_1+11<a_2+11<a_3+11<...<a_{84}+11<=167$
5.我们把两个序列合起来看:
- $a_1,a_2,a_3,...,a_{84},a_1+11,a_2+11,a_3+11,...,a_{84}+11$
- 一共$168$个数。其中每一个数都是$1$到$167$之间的一个整数。
6.**根据鸽巢原理可得,其中必有两个数相等!!!**
7.既然
- $a_1,a_2,a_3,...,a_{84}$
- 中必然无相等的两个数,
- 那么$a_1+11,a_2+11,a_3+11,...,a_{84}+11$
- 中同理。那么,必然存在一个$x$和一个$y$,使得
- $a_x=a_y+11$;
8.从而得出结论:这个$oier$在第
- $y+1,y+2,y+3,...,x$
- 天内一共刷了$11$道题
------------
# 应用二
**证明:在边长为$2$的等边三角形中放上$5$个点。则至少存在两个点,他们之间的距离小于等于$1$.**
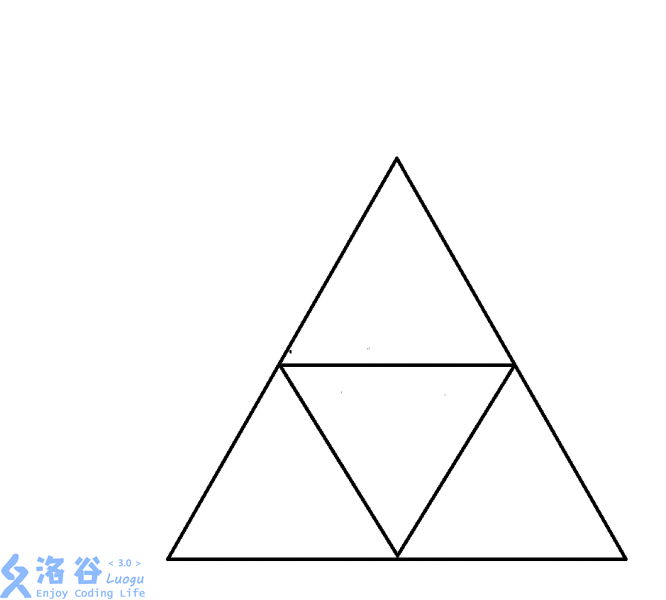
1.我们先画出一个边长为$2$的等边三角形。
2.然后把三条边中点两两相连。就形成了这张图。
3.那么根据鸽巢原理,必然有两个点在一个边长为$1$的小三角形里。
4.而我们知道,边长为$1$的等边三角形里处处距离都小于等于$1$
5.于是问题就解决了
------------
# 应用三
**已知$n+1$个正整数,它们全都小于或等于$2n$,证明当中一定有两个数是互质的。**
1.要证明这个问题,我们就要利用一个互质的特性:两个相邻整数互质。
2.有了这个突破口,于是我们可以构造n个鸽巢,每一个里依次放入
- $1,2,3,...,2n$
- 这2n个数中的两个数。
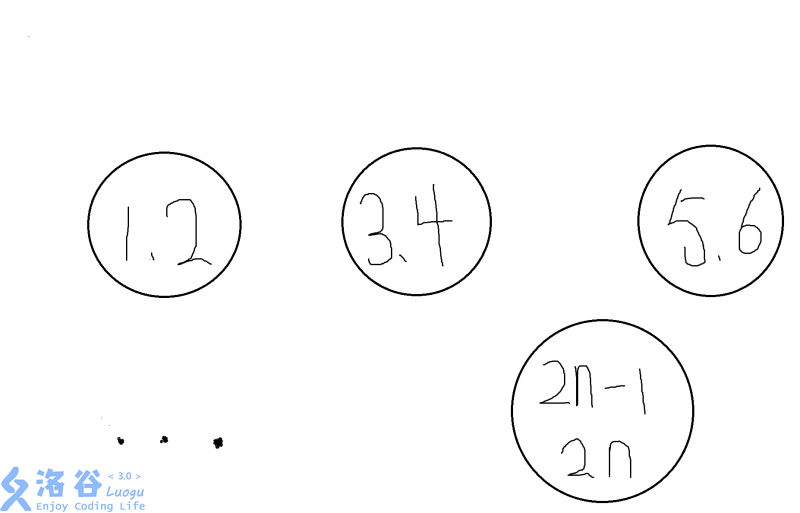
3.也就是说,我们要在这其中取出$n+1$个数。
4.根据鸽巢原理,无论如何,我们都会抽空一个鸽巢。
5.一个鸽巢中的两个数肯定互质,所以问题就解决了。
**扒栗史**:匈牙利大数学家厄杜斯(PaulErdous,1913 - 1996) 向当年年仅$11$岁的波萨(LouisPósa)提出这个问题,而小波萨思考了不足半分钟便能给出正确的答案。
------------
**有趣的小(leng)知(xiao)识(hua)**:
山东高考$2017$年有$54$万人。而人的头发大约有$8-12$万根。那么必然有两人的头发数量相同。
好了,现在来一道初赛真题收(dian)心(di):
**【NOIP2010 提高组】记$T$为一队列,初始时为空,现有n个总和不超过$32$的正整数依次入队,如果无论这些数具体为什么值,都能找到一种出队的方式,使得存在某个时刻队列$T$中的数之和恰好为$9$,那么$n$的最小值是_______________**
1.第一眼看到此题,蒟蒻就知道自己只能~~根据结果推过程~~了
2.刚开始看了一眼答案:$18$.
3.于是就根据这个开始推导过程。我们可以令$a_i$表示前$i$个数的和,并约定:$a_0=0$.
4.题目要求求出最小的$n$,使得存在$0<=x<y<=n$满足$a_y=a_x+9$;
5.于是我们可将$a$数组看做鸽子,用不能同时取的一组(差为$9$)的集合构造笼子,
6.构造方法如下:一共有$n=18$个集合按此方式选取:
- ${0,9}、{1,10}、{2,11}、...、{8,17}、{18,27}、{19,28}、{20,29}、...、{23,32}、{24}、{25}、{26}$。
7.由题意可知,我们一旦在某个集合中取了两个元素,$then$ 一定存在某个时刻队列$T$中数的总和恰好为$9$.
8.于是由鸽巢原理,我们可以得知:$n=18$一定满足条件.
**但是题目要让我们求出最小值,为了保险起见(都看答案了还保什么险):**
1.我们还要证明一下$n=17$不可行。
2.然鹅我们只需要举出反例即可:
- 1 1 1 1 1 1 1 1 10 1 1 1 1 1 1 1 1
3.说明:因为每到了$8$个$1$就被$10$隔断,故不可行。
------------
# 第二部分:Ramsey定理
**扒栗史**:此定理由Frank Plumpton Ramsey(弗兰克·普伦普顿·拉姆齐,$1903-1930$)提出.
- 此定理有一个广为流传的例子:6 个人中至少存在3人相互认识或者相互不认识。
- 转换:该定理等价于证明这6个顶点的完全图的边,用红、蓝二色任意着色,必然至少存在一个红色边三角形,或蓝色边三角形
证明如下:
1、首先,把这6个人设为A、B、C、D、E、F六个点。由A点可以引出AB、AC、AD、AE、AF五条线段。
2、设:如果两个人认识,则设这两个人组成的线段为红色;如果两个人不认识,则设这两个人组成的线段为蓝色。
3、由鸽巢原理可知:这五条线段中至少有三条是同色的。不妨设AB、AC、AD为红色。若BC或CD为红色,则结论显然成立。若BC和CD均为蓝色,则若BD为红色,则一定有三个人相互认识;若BD为蓝色,则一定有三个人互相不认识。
**以下部分正在补充,本文未完成**
###### 后记:部分内容来自于一本通