ARC167E One Square in a Triangle
樱雪喵
·
·
题解
也许会更好的阅读体验
Description
多组询问,每次给定一个数 S,要求构造一个符合如下条件的三角形:
- 三角形的顶点都在格点上;
- 面积为 \frac{S}{2};
- 恰好包含了一个顶点在格点上的 1\times 1 的正方形(换句话说,恰好包含一个完整的格子)
## Solution
做法参考部分题解,画了几个图。
设三角形的三个顶点分别为 $a,b,c$。整体平移这个三角形不影响答案,所以钦定 $a=(0,0)$ 以简化计算。
首先 $S$ 为偶数的情况,我们可以钦定三角形的底为 $2$,令 $a=(0,0),b=(2,0),c=(\frac{S}{2},\frac{S}{2})$。
这在 $S\ge 4$ 的情况下可以看出是对的,而手玩可以发现 $S=2$ 无解。
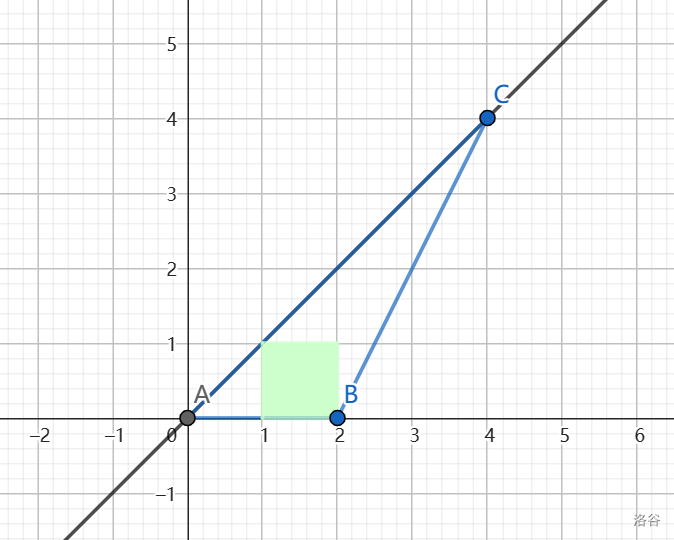
考虑 $S$ 为奇数的情况。类比偶数时答案的形态:我们确定一条底边,并让剩下的一个点在某条直线上移动。
设 $b=(x_b,y_b),c=(x_c,y_c)$,根据三角形的面积公式(可以根据叉积的几何意义证),有
$$ S=|x_b y_c - x_c y_b| $$
$S$ 是奇数,则 $x_b y_c$ 与 $x_c y_b$ 有一个是奇数,即要么 $x_b,y_c$ 都是奇数,要么 $x_c,y_b$ 都是奇数。令 $b=(3,1)$。
那么式子变成了 $S=|3y_c - x_c|$。
要令 $3y_c$ 和 $x_c$ 的奇偶性始终不同,考虑钦定 $y_c=x_c+1$。答案即为 $a=(0,0),b=(3,1),c=(\frac{S-3}{2},\frac{S-1}{2})$。
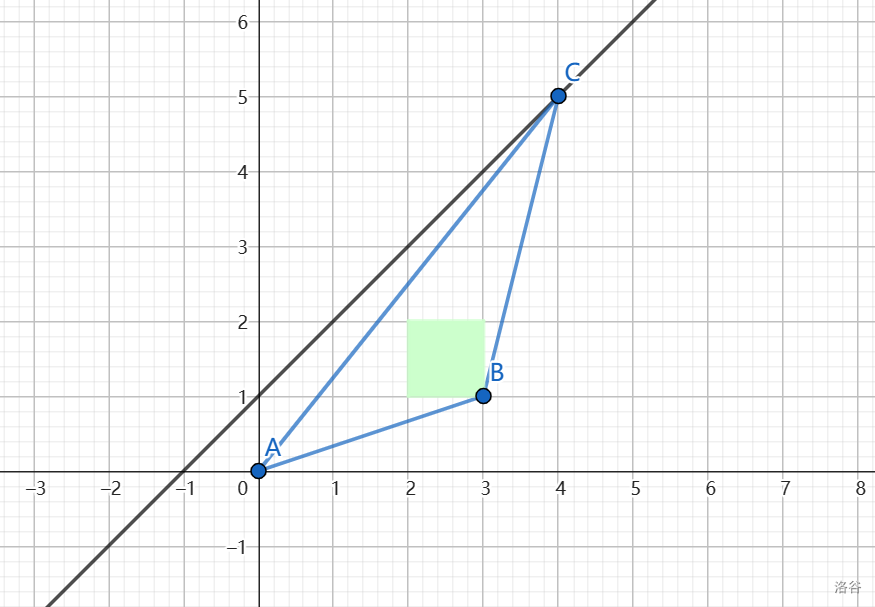
如图,在 $S\ge 9 $ 时满足条件。
手玩小于 $9$ 的情况,发现 $S=1,3,5,7$ 均无解。
```cpp
int T,S;
int main()
{
T=read();
while(T--)
{
S=read();
if(S<9&&(S&1)||S==2) {printf("No\n");continue;}
printf("Yes\n");
if(S&1) printf("0 0 3 1 %d %d\n",(S-3)/2,(S-1)/2);
else printf("0 0 2 0 %d %d\n",S/2,S/2);
}
return 0;
}
```