题解 P3369 【【模板】普通平衡树】
arfa
·
·
题解
强势图解 \texttt{FHQ Treap}。
首先说一说 \texttt{FHQ Treap} 的优点,好理解,上手快,代码一般很短,可持久化等。
重要的是不用旋转。
$\texttt{Split}$ 的意思就是将这颗二叉树按某种条件掰开两半。这道题是按权值的大小掰开。假如一棵树要以 $\texttt{6}$ 来掰开,如图 : (下方都是 $tree$ 值)
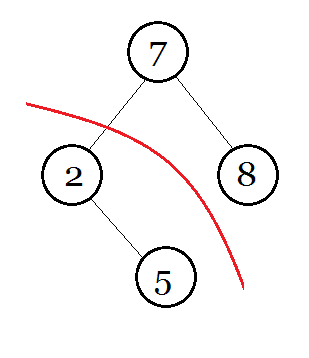
然后大力开花
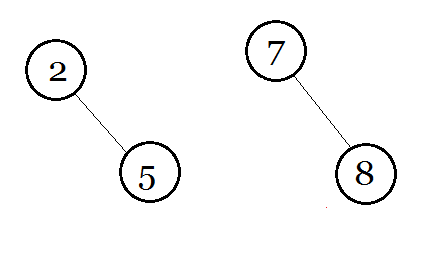
约定 : 分裂后左边的树为 $x$,右边的树为 $y$,它们的根为 $X$ 和 $Y$。
那么合并呢? 就是大力将两棵树合在一起。
那么这两个操作有什么用呢?
$$\large\texttt{Insert}$$
首先是插入一个数字 $k$。
我们想,如果我们按照 $k$ 掰开整颗树,然后将 $k$ 强行套进去,然后再合起来是不是就可以呢了。
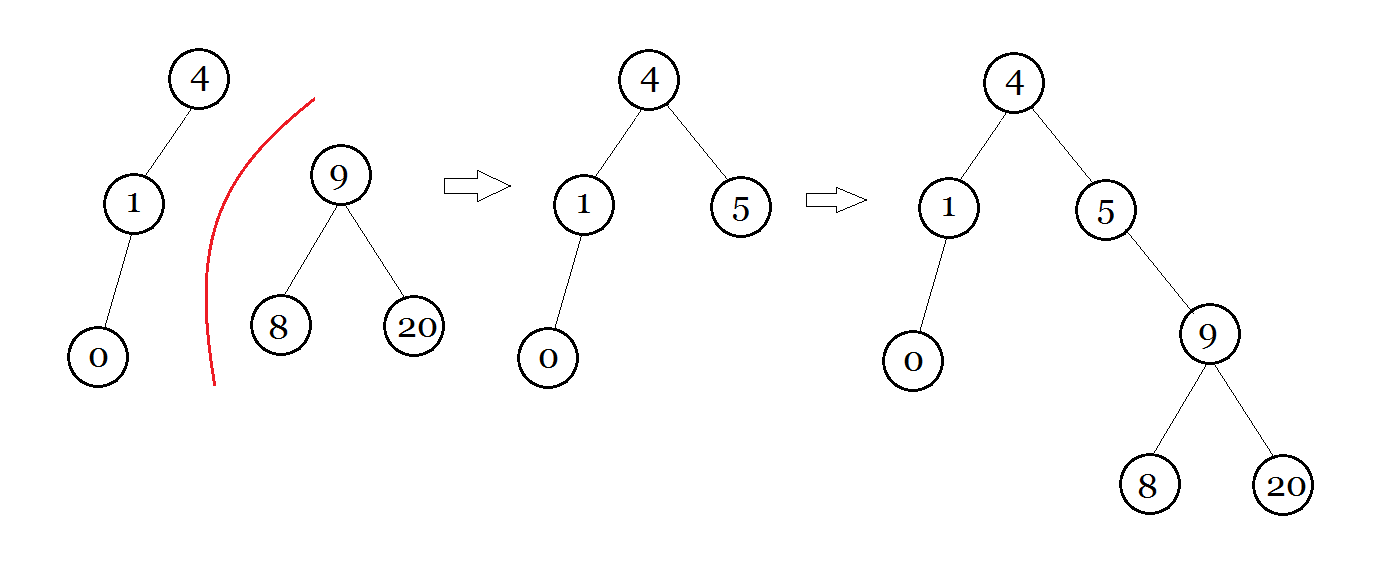
图解 : (假如 $\texttt{Insert}\ 5$)
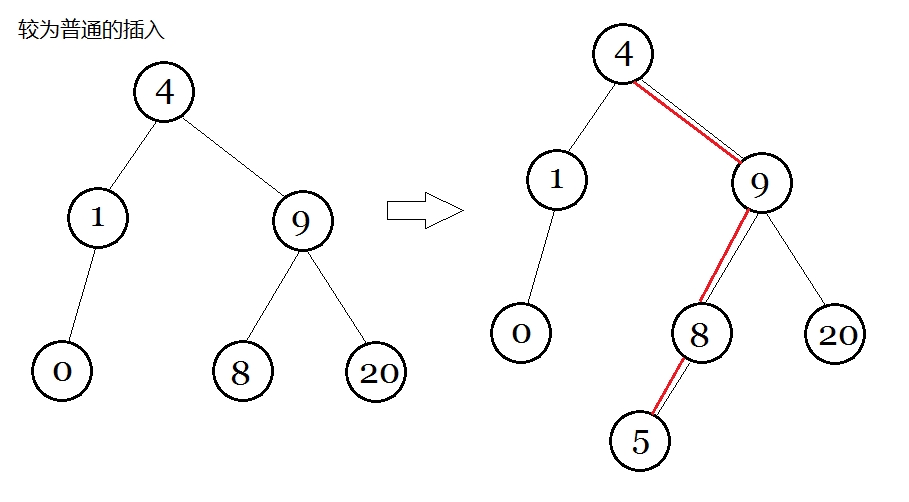
然后是 $\texttt{FHQ Treap}$ 的插入 (博主没有考虑 $heap$ 值,所以大家先感性理解)
代码?
```pascal
procedure Insert(val:longint);
var x,y,o:longint;
begin
x:=0; y:=0; Add(val); o:=n; // 新建一个节点,左树的根为 x,右树的根诶 y
Split(root,x,y,val); // 这一个分裂操作会返回 x,y,还会将一些边改变
Merge(x,x,o); Merge(root,x,y); // 将 x 树和新节点合并,形成的新树跟 y 节点合并
end;
```
我们可以依赖 $\texttt{Merge}$ 来维护堆的性质。
$$\large\texttt{Delete}$$
众所周知,$\texttt{BST}$ 的删除无比麻烦。
$\texttt{FHQ Treap}$ 可真是嗨到不行。
我们可以知道,如果我们把一个点的左儿子和右儿子合在一起,那么这个点就会变成 $\texttt{JO}$ 极生物。
我们要删除节点 $k$。
首先我们要把这棵树分成以 $k$ 领导的树和非 $k$ 领导的树,就是大力掰开。然后把以 $k$ 领导的树的左儿子和右儿子合起来,将 $k$ 丢入虚无。然后再合并新合成的树和非 $k$ 领导的树。
图解 : (假如我们 $\texttt{Delete}\ 9$)
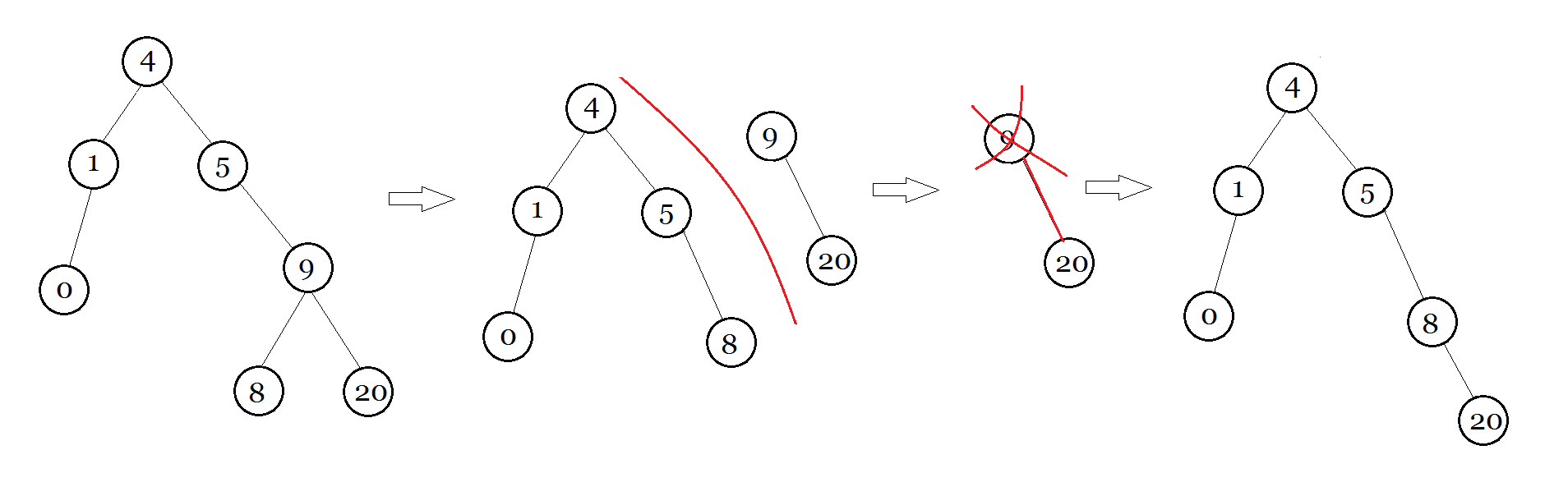
```pascal
procedure Delete(val:longint);
var x,y,o:longint;
begin
x:=0; y:=0; o:=0;
Split(root,x,y,val); // 分裂成 x,y 树
Split(x,x,o,val-1); // 分裂成 x',o 树
Merge(o,son[o,0],son[o,1]); // 将 o 树的根干掉,然后变成新的 o 树
Merge(x,x,o); // o+x' 树=x树
Merge(root,x,y); // x+y树
end;
```
$$\large\texttt{Query}$$
这个操作是查询第 $K$ 大,要按照普通的查询方法来搞。
```pascal
function Query(now,k:longint):longint;
begin
Query:=0;
if size[son[now,0]]+1=k then exit(tree[now]);
if size[son[now,0]]>=k then Query:=Query(son[now,0],k) else
Query:=Query(son[now,1],k-size[son[now,0]]-1);
end;
```
$$\large\texttt{Rank}$$
求数字 $k$ 的排名。
我们再次大力掰开,把 $k-1$ 这个点拿出来。这个时候根 $x$ 都是 $\leq k-1$ 的 (也就是 $< k$)。然后我们把它的 $size$ 拿出来,加个一就好了。
```pascal
function Rank(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k-1);
Rank:=size[x]+1; Merge(root,x,y);
end;
```
$$\large\texttt{Precursor}$$
求数字 $k$ 的前缀。
你按照 $k-1$ 掰开这棵树,就可以保证这棵树都是 $< k$ 的,然后找最大值。
图解 : ($\texttt{Precursor}\ 5$)
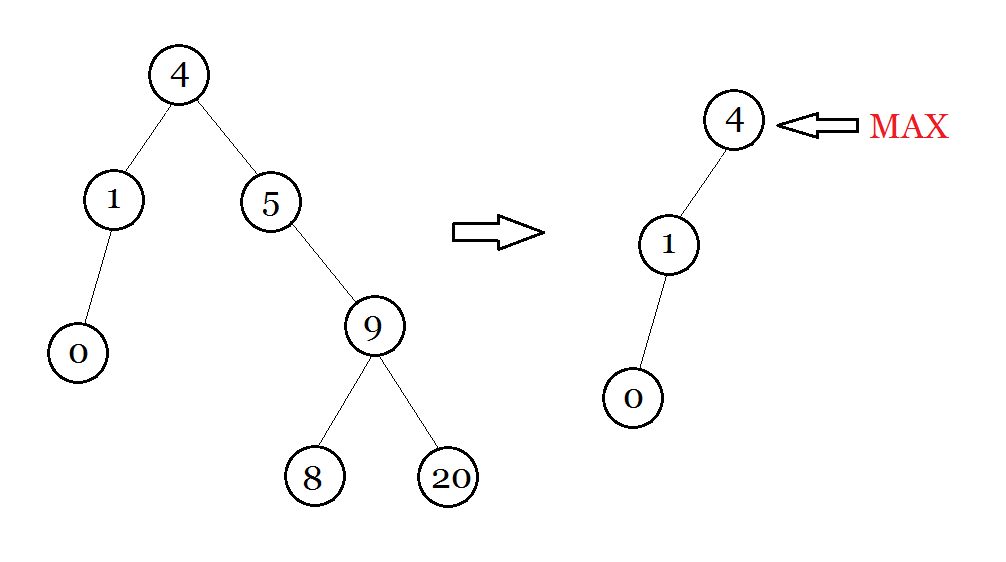
```pascal
function Precursor(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k-1);
Precursor:=Query(x,size[x]);
Merge(root,x,y);
end;
```
$$\large\texttt{Next}$$
求数字 $k$ 的后继。
你按照 $k$ 掰开这棵树,就可以保证这棵树都是 $\ge k$ 的,然后找最小值。
```pascal
function Next(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k);
Next:=Query(y,1);
Merge(root,x,y);
end;
```
$$\large\texttt{Split}$$
激动人心的时候到了。
$son[i,0/1]$ 为左右儿子。
按照 $tree$ 来分裂。
图解 : (红色圈代表现在所在的节点,蓝色、橙色代表经过红色圈后所推出这一部分在左树还是右树,灰色代表未知)
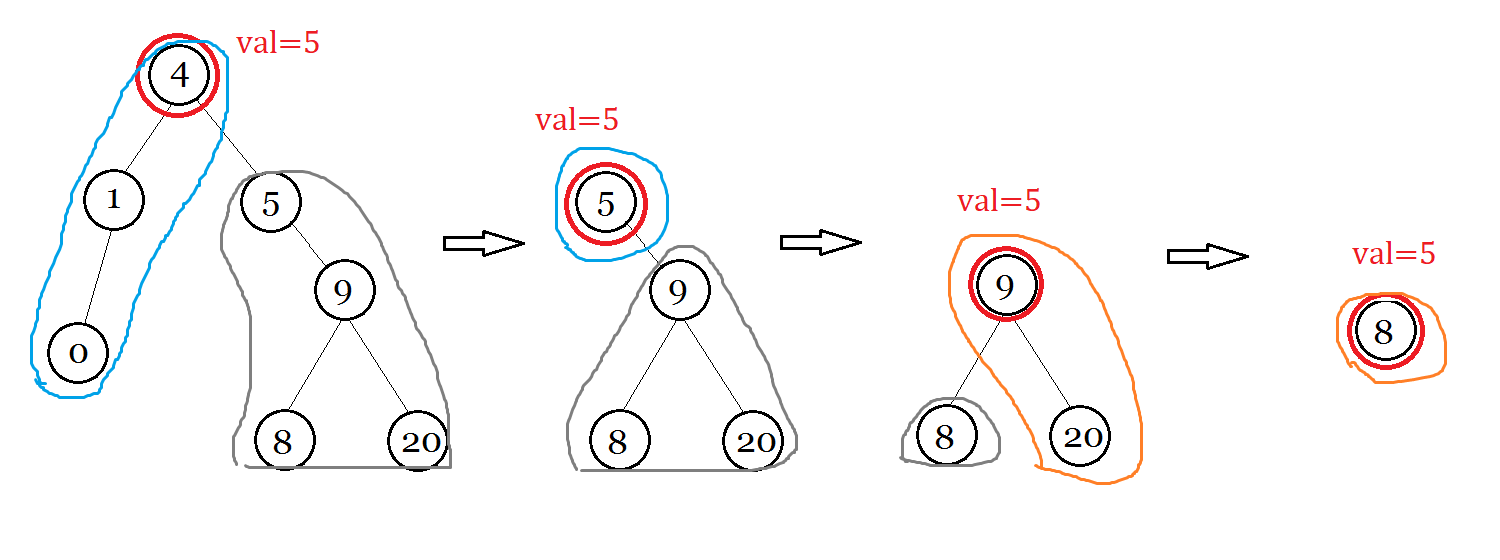
```pascal
procedure Split(now:longint;var a,b:longint;val:longint);
begin
// now 为现在的节点,a,b 为分裂的树,val 为要掰开的值
if now=0 then begin a:=0; b:=0; exit; end; // 结束分裂
if tree[now]<=val then // 如果这个 tree 值要放在左边
begin a:=now; Split(son[now,1],son[a,1],b,val); end // 那么这个树 a 的右儿子还是可能会大于 val 的,所以给 b
else begin b:=now; Split(son[now,0],a,son[b,0],val); end; // 同理
size[now]:=size[son[now,0]]+size[son[now,1]]+1;
end;
```
注意,$\texttt{Split}$ 会让整棵树分为两棵树 (连边上),然后会返回两个权值为两棵树的根。
一次分裂的时间复杂度为 $O(Height)$,期望为 $O(\log N)$。 (如果你将大佬的生日编入随机,那么你的期望效率将会大大提升)
$$\large\texttt{Merge}$$
满足 $heap$ 来合并。
因为分裂成 $x,y$ 树,那么 $y$ 树中的任意一个点的值肯定是大于 $x$ 树的。因此我们只需要确定父子关系,这由 $heap$ (小根堆) 决定。如果 $x$ 中的某点的 $a$ 的 $heap$ 小于 $y$ 中的 $b$ 的 $heap$,那么 $b$ 肯定是 $a$ 的右儿子,反之 $a$ 为 $b$ 的左儿子。
图解 : (以下圈外是 $heap$ 值,橙色部分为被选入儿子的部分)


这样一次的时间复杂度最多是 $O(x_{Height}+y_{Height})$,期望也是 $O(\log N)$。
```pascal
procedure Merge(var now:longint;a,b:longint);
begin
if (a=0)or(b=0) then begin now:=a+b; exit; end; // 一个树为空了,另一个树整体插入
if (heap[a]<heap[b]) then // 如果 a 树为 b 树的父亲,
// 又因为 b 树肯定是大于 a 树的,所以 b 树是 a 树的右后代,继续往右边合并,而左儿子不管
begin now:=a; Merge(son[now,1],son[a,1],b); end
else begin now:=b; Merge(son[now,0],a,son[b,0]); end; // 同理
size[now]:=size[son[now,0]]+size[son[now,1]]+1;
end;
```
$$\large\texttt{Code}$$
```pascal
Uses math;
Const
RP=2006212;
total=100010;
var
size,tree,heap:array[-1..total*2] of longint;
son:array[-1..total*2,-1..2] of longint;
i,m,n,k,root,order:longint;
procedure Add(val:longint); begin inc(n); size[n]:=1; tree[n]:=val; heap[n]:=random(RP); end;
procedure Split(now:longint;var a,b:longint;val:longint);
begin
if now=0 then begin a:=0; b:=0; exit; end;
if tree[now]<=val then
begin a:=now; Split(son[now,1],son[a,1],b,val); end
else begin b:=now; Split(son[now,0],a,son[b,0],val); end;
size[now]:=size[son[now,0]]+size[son[now,1]]+1;
end;
procedure Merge(var now:longint;a,b:longint);
begin
if (a=0)or(b=0) then begin now:=a+b; exit; end;
if (heap[a]<heap[b]) then
begin now:=a; Merge(son[now,1],son[a,1],b); end
else begin now:=b; Merge(son[now,0],a,son[b,0]); end;
size[now]:=size[son[now,0]]+size[son[now,1]]+1;
end;
procedure Insert(val:longint);
var x,y,o:longint;
begin
x:=0; y:=0; Add(val); o:=n;
Split(root,x,y,val);
Merge(x,x,o); Merge(root,x,y);
end;
procedure Delete(val:longint);
var x,y,o:longint;
begin
x:=0; y:=0; o:=0;
Split(root,x,y,val); Split(x,x,o,val-1);
Merge(o,son[o,0],son[o,1]);
Merge(x,x,o); Merge(root,x,y);
end;
function Query(now,k:longint):longint;
begin
Query:=0;
if size[son[now,0]]+1=k then exit(tree[now]);
if size[son[now,0]]>=k then Query:=Query(son[now,0],k) else
Query:=Query(son[now,1],k-size[son[now,0]]-1);
end;
function Rank(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k-1);
Rank:=size[x]+1; Merge(root,x,y);
end;
function Precursor(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k-1);
Precursor:=Query(x,size[x]);
Merge(root,x,y);
end;
function Next(k:longint):longint;
var x,y:longint;
begin
x:=0; y:=0; Split(root,x,y,k);
Next:=Query(y,1);
Merge(root,x,y);
end;
begin
randomize; root:=1; Add(maxlongint); heap[root]:=-maxlongint;
read(m);
for i:=1 to m do
begin
read(order,k);
Case order of
1 : Insert(k);
2 : Delete(k);
3 : writeln(Rank(k)); // Get num's rank
4 : writeln(Query(root,k)); // Get rank's num
5 : writeln(Precursor(k));
6 : writeln(Next(k));
end;
end;
end.
```
本文可能会有细节错误 ~~(有锅)~~ 之类的,已有发现敬请提出。
博主书写不易,敬请单连。关于一些奇奇怪怪的东西,请看 :[关于普通平衡树的均摊复杂度的优化](https://www.luogu.org/blog/acking/guan-yu-pu-tong-ping-heng-shu-di-jun-tan-fu-za-du-di-you-hua)。