abc 232 e 题解
Yan719
·
·
题解
abc 232 e
题意
有一个 n \times m 的矩阵,一开始有个物品放在 (x_1, y_1) 上。
有 k 次操作,每次操作可以将这个物品移动到同一行或者同一列的另一个格子上。
请你求出在 k 次操作后,使得这个物品到达 (x_2, y_2) 的方法有多少种,对 998244353 取模。
思路
首先,这道题我们先考虑暴力。
那么就有转移:
$$dp_{x, y, k} = \sum _ {x' = x, y' \ne y} dp_{x', y', k - 1} + \sum _ {x' \ne x, y' = y} dp_{x', y', k - 1}$$
所以,状态总数为 $n \times m \times k$,每次有 $n + m$ 种转移,总时间复杂度为 $O(n \times m \times k \times (n + m))$,也就是 $10 ^ {33}$,很明显会超时。
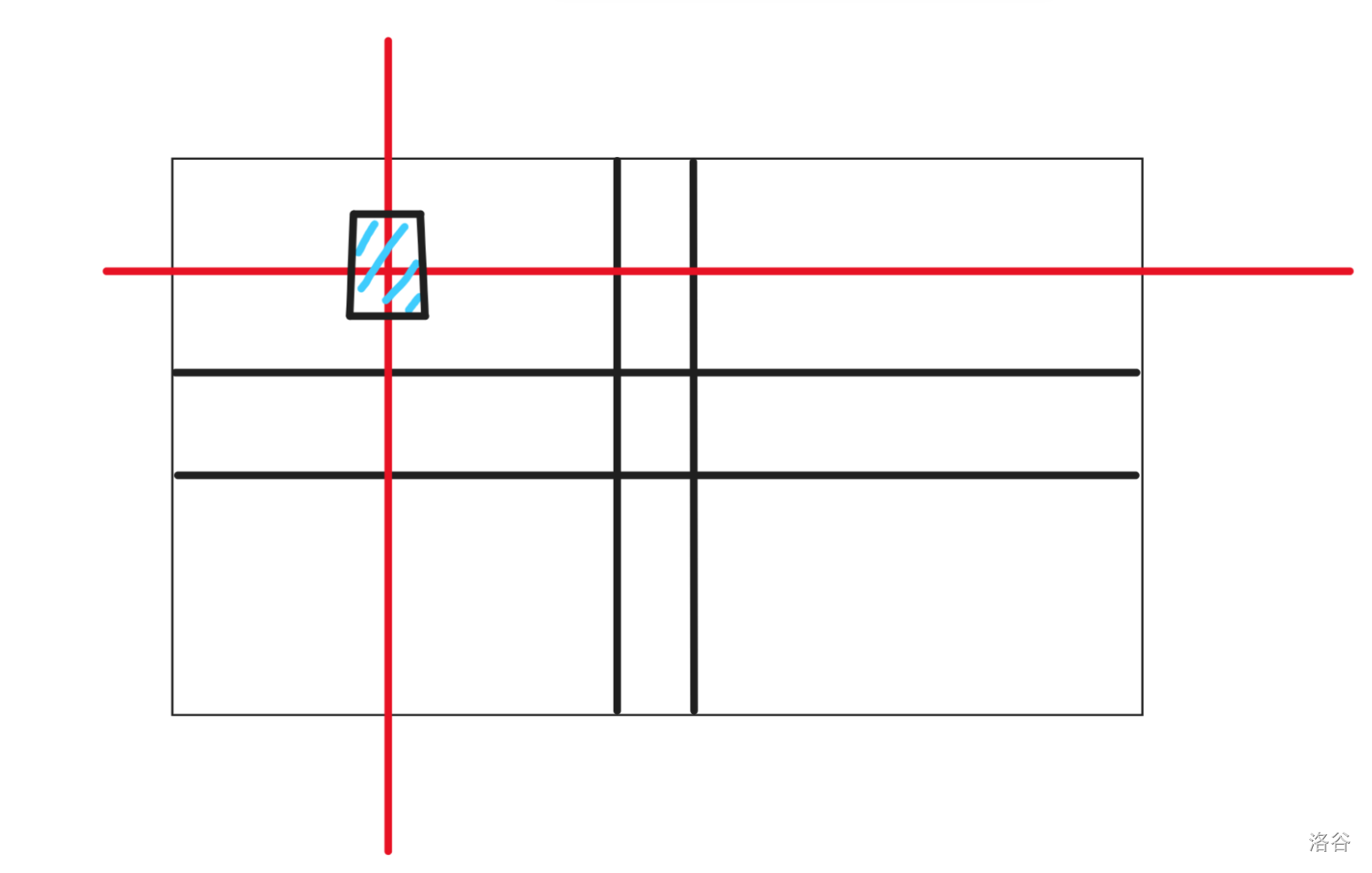
通过打表输出 `dp` 数组,我们可以发现,整个矩阵最后的结果一共可以分为四种:
1. 起点
2. 和起点同行的点
3. 和起点同列的点
4. 和起点不同行也不同列的点
所以,$dp_{k, 0}$ 表示用 $k$ 步走到起点的方案数,$dp_{k, 1}$ 表示用 $k$ 步走到与起点同行的其他的点的方案数,$dp_{k, 2}$ 表示用 $k$ 步走到与起点同列的其他的点的方案数,$dp_{k, 3}$ 表述用 $k$ 步走到和起点不同行也不同列的点的方案数。
那么,转移是什么呢?
我们可以画一个图来看一看。
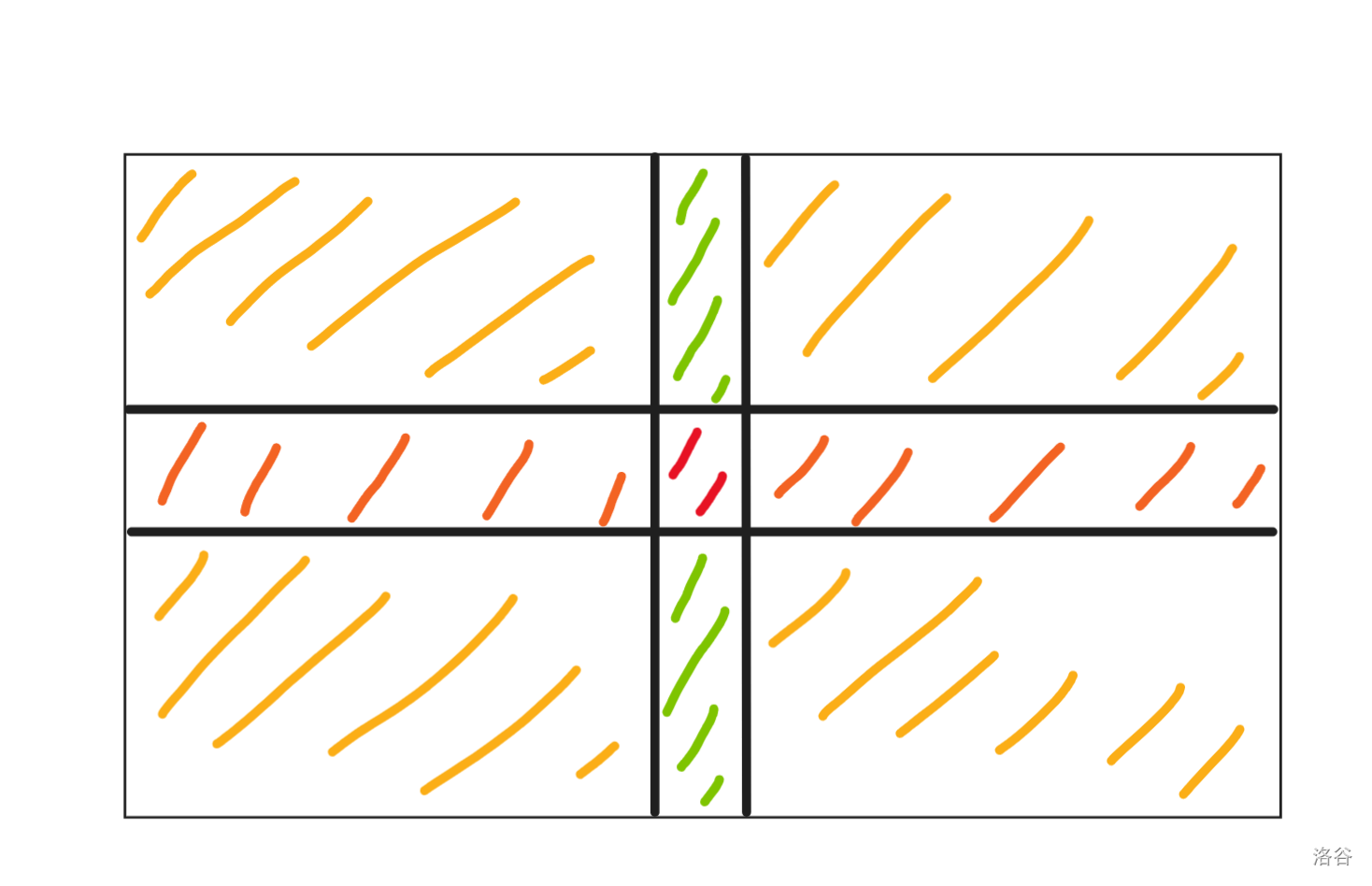
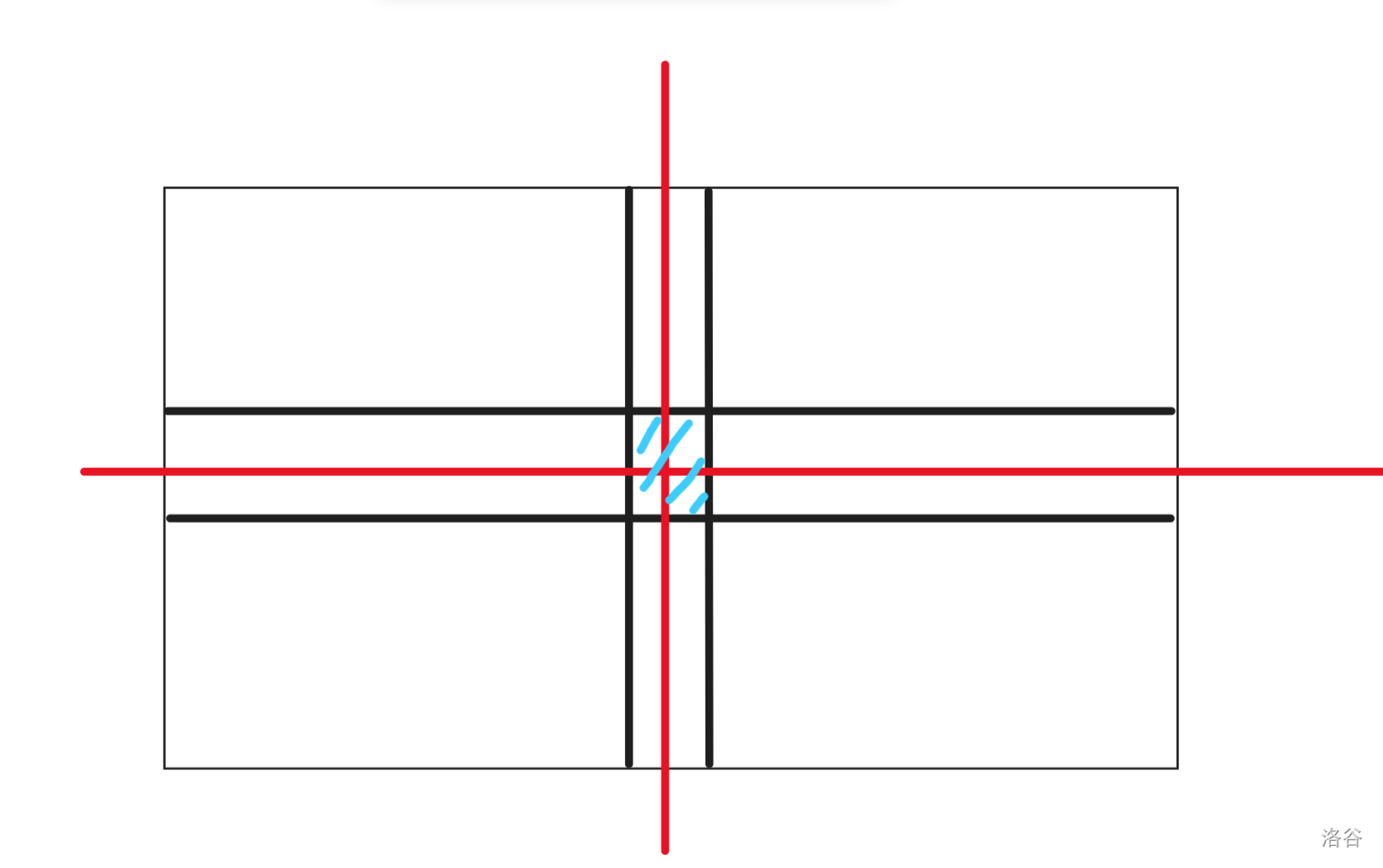
$$dp_{k, 0} = dp_{k - 1, 1} \times (m - 1) + dp_{k - 1, 2} \times (n - 1)$$
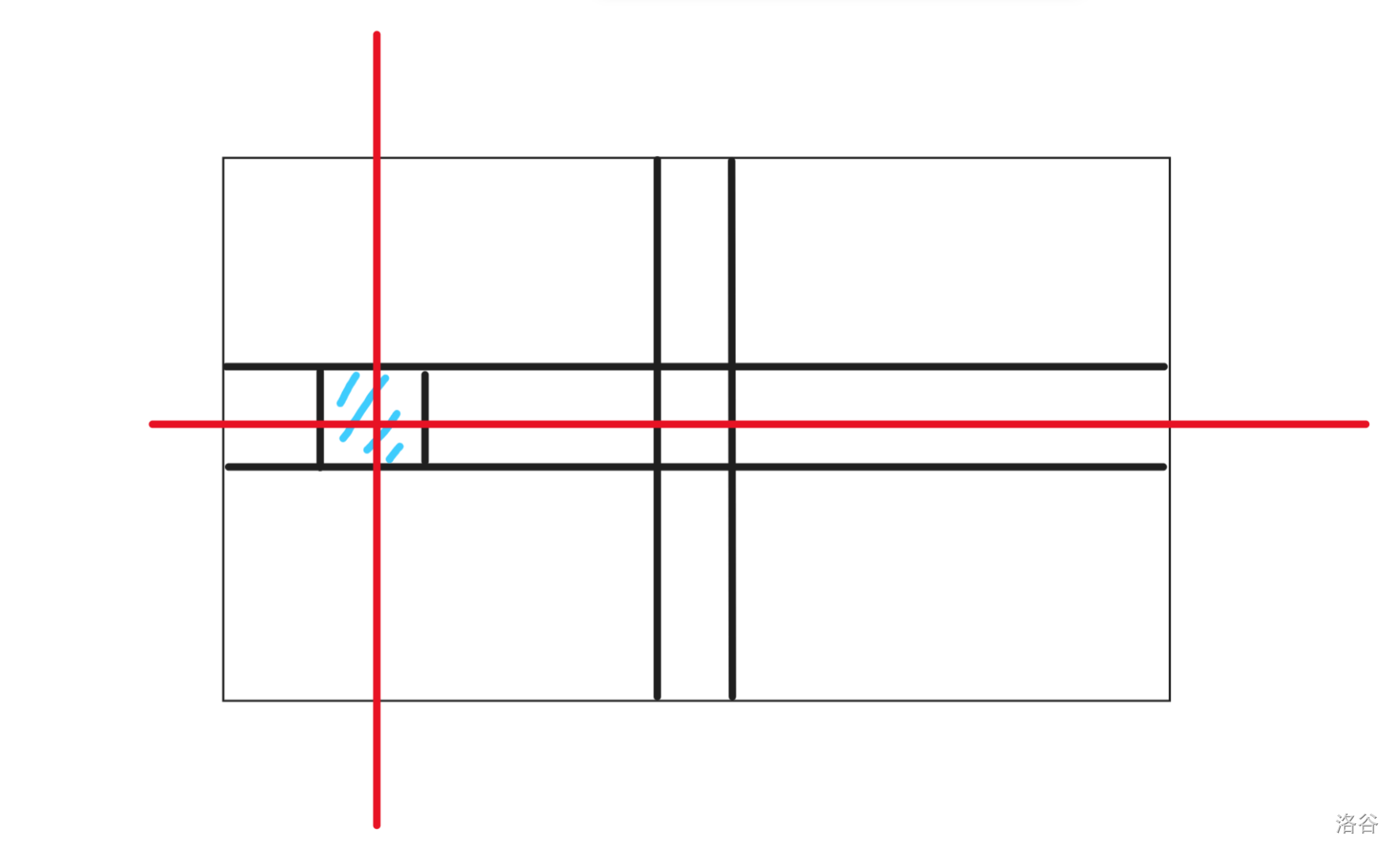
$$dp_{k, 1} = dp_{k - 1, 0} + dp_{k - 1, 1} \times (m - 2) + dp_{k - 1, 3} \times (n - 1)$$
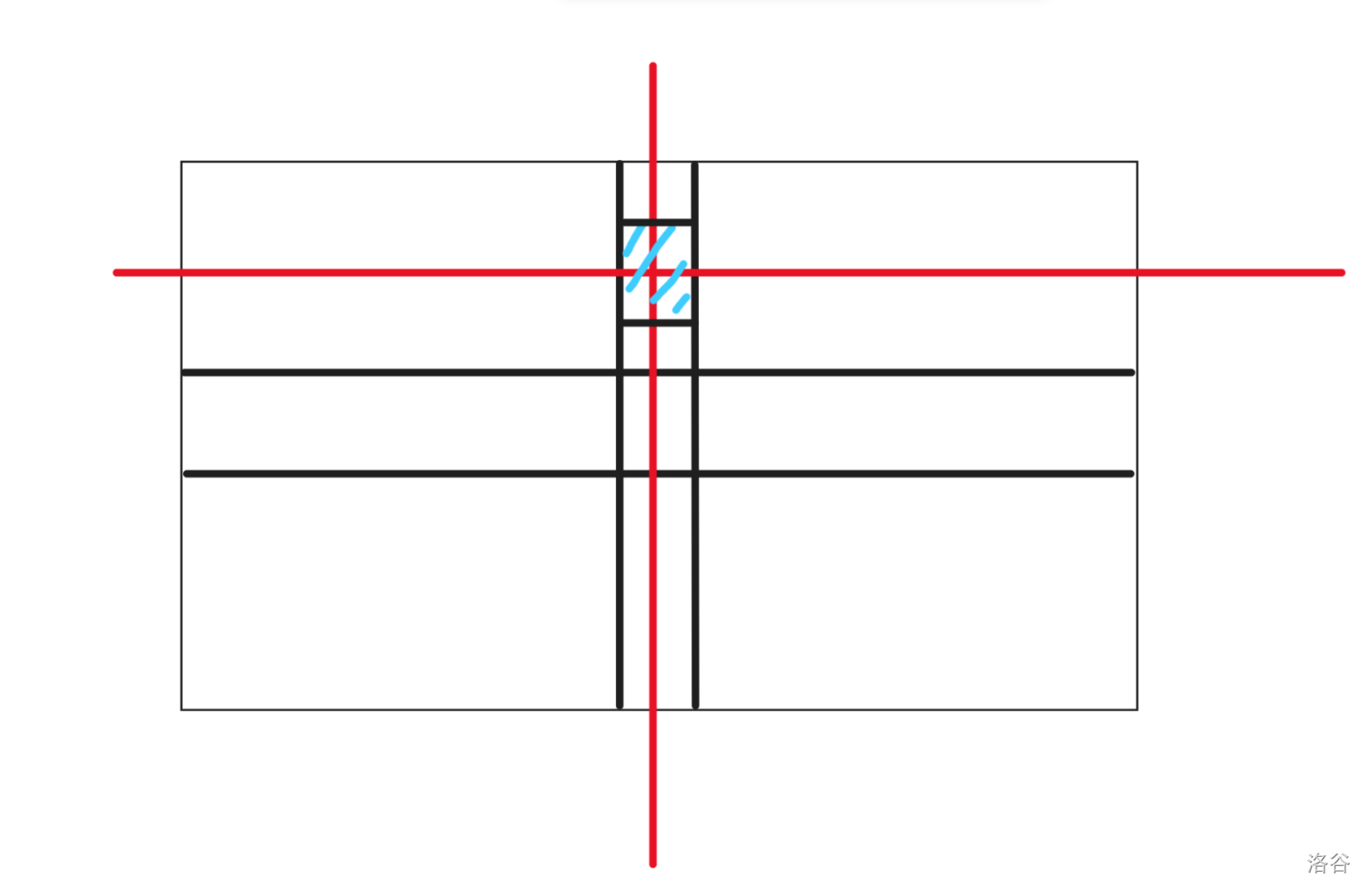
$$dp_{k, 2} = dp_{k - 1, 0} + dp_{k - 1, 2} \times (n - 2) + dp_{k - 1, 3} \times (m - 1)$$
$$dp_{k, 3} = dp_{k - 1, 1} + dp_{k - 1, 2} + dp_{k - 1, 3} \times (n + m - 4)$$
所以,时间复杂度为 $O(k)$。