[题解]UVA11270 Tiling Dominoes

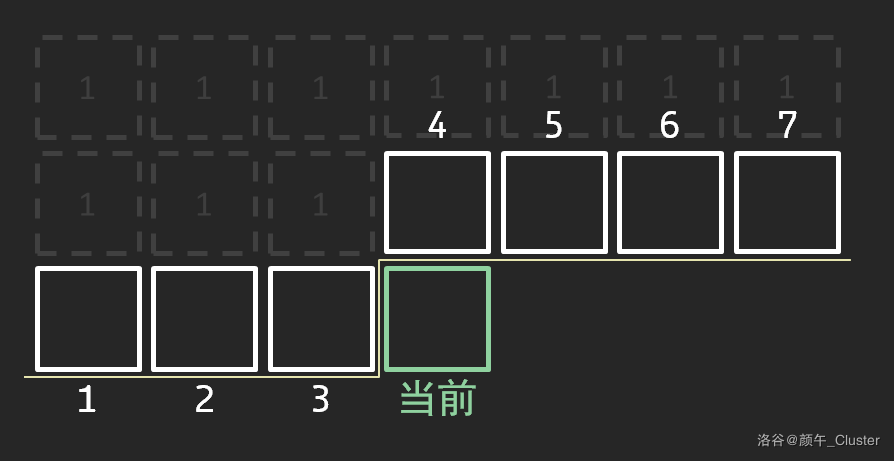
[](https://www.luogu.com.cn/problem/UVA11270) ------------ 看到了很多dalao发的题解，但是理解得不是特别清楚，研究了一下午终于懂了(:D) 这里我们**逐格**进行DP。但记录的状态是各行内的**轮廓线**上格子的覆盖情况。 $f[i][s]$表示第i行的轮廓线状态为s时的方案数。 轮廓线……是啥？ 请看下图  图中绿色格子为$\color{LimeGreen}\text{当前}$推到的格子。那条金黄色亮闪闪的线就是$\color{Goldenrod}\text{轮廓线}$。 我们用格子所在的列数 来给轮廓线上方的格子（白色格子）编号。编完号后即可二进制**状态压缩**，用1表示被覆盖，用0表示未被覆盖。 如图： （由于数字的一般为从高到低，便于与图示对应我们这里采用“逆写法”）  按照题目的设定，要 _覆盖整个网格_ ，**轮廓线之上的所有格子都应该是1**，**但**！**是**！由于考虑到有**竖放**的骨牌，我们使与轮廓线相邻的这些方格（白色）中能够存在0，起到一个类似“缓冲？”的作用。$\color{red}\text{<重点1>}$（具体的意思可以看下文） 好，状态表示完毕，接下来我们来看转移的方法 显然，对于当前格（绿），只有3种决策： >1.竖放（向上） > >2.横放（向左） > >3.留空 **设白色格内的状态为$k$，转移后为$k'$** **设绿色格所在列数为$j$** **仅第$x$位为1的状态为$p[x]\quad$** (即1<<(x-1))  我们来分类讨论： ### 1.竖放： 什么时候需要竖放呢？$\quad$应该观察当前格**上方**的格子状态。 当前格上方的状态用数据表示即为$k \& p[j]$ - 如果当前格上方为**0**,那么**必须放一个竖放的骨牌** 为什么呢？因为上方白色格子的内容是**已经确定**的，也就是说，此时不放一块向上的骨牌，那么上方这个格子就会**永远无法被覆盖**,这与题目要求的**覆盖整个网格**不符。因此必须放一个竖向骨牌$\color{red}\text{<重点2>}$ - 那么当前格上方为**1**,那么你肯定**无法**放一个向上的骨牌。 **综上**，若上方为0则放置竖向骨牌(!(k&p[j])) 同时，当前格也**不能位于第一行**。(j>1) 接下来我们来整个转移方程出来。 上图  在经过转移后，我们的动规推进了一格，**k的第j位在推进前后，从当前格的上一个格子，变成了当前格本身(观察左下角的格子排列)**(理解这一点很重要(至少对于我自己来说))$\color{red}\text{<重点3>}$ 即k的第j位 从0变成了1，而原来的上方格子则不用再考虑了 >#或许你可以停下来思考一下…… 由于求的是总方案数，因此转移时采用**加和**，初始化为0。 因此，状态转移方程如下: $${\text{if}((i>1)\, \&\&\,!(k\&p[j]))}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$$ $$ k'=k|p[j]$$ $$ f[i][k']+=f[i-1][k] $$ ### 2.横放： 现在有了第一种的经验，我们可以依样画葫芦，轻松地推出其他的情况 >#试着自己推一推？ 情况1中我们已经得知，**如果上方的格子未被覆盖，则必定要放一个竖向骨牌将其填满**(重点2处)。即下文条件2. 横放的条件是 1. 左侧格子没有被覆盖(!(k&q[j-1])) 2. 上方的格子已经被覆盖(k&q[j]) 3. 不在第一列(j>1) 而具体的转移方法 则是 横放后$k'$的第$j$位(本身)与第$j-1$位(左侧格子)都应该是**1**。而由条件2可知原k的第$j$位原来就是**1**，故只需要将左侧格子改为1。 状态转移方程： $${\text{if((j>1) \&\& !(k\&q[j-1]) \&\& (k\&q[j]))}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$$ $$ k'=k|p[j-1]$$ $$ f[i][k']+=f[i-1][k] $$ ### 3.留空： 同情况2条件2，只有在上方格子被覆盖的情况下，才可以进行除了竖放以外的操作，而对于留空，则没有什么要求。 则条件是： 1. 上方的格子已经被覆盖(k&q[j]) 转移方法则是$k'$的第$j$位改为0； $${\text{if(k\&q[j])}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad$$ $$ k'=k\; xor\; p[j-1]$$ $$ f[i][k']+=f[i-1][k] $$ >#思考 留空 与 竖放 的关系 #### 可以结合下面这张图来理解。  初始化为f[0][(1<<m)-1]=1; （把第0行填满） 最终答案为f[d][(1<<m)-1]; (最后一行填满) ### 一些优化 - 由于每一行的状态仅有上一行推出，且最终只取最后一行，可以使用2行的**滚动数组**优化； - 预处理p数组(即1<<(i-1)); - 防止**状态压缩**超出整数范围，始终保证n>m,使m≤10； ### 代码 ```cpp #include<bits/stdc++.h> using namespace std; int n,m; long long int f[2][(1<<10)]; int p[20]; int main(){ for(int i=1;i<=15;i++){ p[i]=1<<(i-1); }//预处理 while(~scanf("%d %d",&n,&m)) { if(n<m) swap(n,m);//交换，使m不大于10 int d=0;//滚动数组下标 memset(f,0,sizeof(f));//清空 f[0][(1<<m)-1]=1;//初始化 for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ d^=1;//d在0与1之间滚动 memset(f[d],0,sizeof(f[d]));//清空 for(int k=0;k<(1<<m);k++){ if(k&p[j]) f[d][k^p[j]]+=f[d^1][k];//留空 if((j>1) && !(k&p[j-1]) && (k&p[j]))//横放 f[d][k|p[j-1]]+=f[d^1][k]; if((i>1) && !(k&p[j])) f[d][k|p[j]]+=f[d^1][k];//竖放 } } } cout<<f[d][(1<<m)-1]<<endl;//最终输出最后一行也填满的情况 } } ```