多项式计数杂谈
command_block
·
2020-02-11 18:16:01
·
算法·理论
Ox00. 前面的话 & 前置芝士
本文 Markdown 源码已达 \rm 128Kb ,且公式较多,可能导致浏览器卡顿,请耐心等待。
本文 60\% 的内容完成于 2020 省选季,其余内容为断断续续更新而得。
记录部分常见经典问题的解法 ( \rm basis )。
介绍一些比较系统的数学知识以形成架构 ( \rm spanning )。
笔者的数学比较菜,理解可能略显东拼西凑,大佬轻喷。
本文不包入门,不包一定能看懂 (如果懵逼请优先考虑前置芝士是否熟悉) ,不保证数学上的完全严谨正确。
本文可能(即将)包含的内容 :
经典微积分和有限微积分基础 (\text{done, may update})
生成函数的引入和简单应用 (\text{done})
OGF,EGF,PGF 的引入,初等工具 (\text{partially completed, paused})
关于组合数求和的一些技巧 (\text{done, may update})
处理生成函数的经典进阶技巧,以及相关工具 (\text{doing})
若干类特殊的数,以及常用结论 (\text{done, may update})
组合结构符号化 (\text{doing})
图计数 (\text{doing})
每一章节内部大致按照难度排序 ,但是章节之间没有难度关系 ,而且知识往往是互相关联引用的,建议在各章节之间跳跃推进 。
出于简洁性考虑,本文不会大量论述题解形式的具体应用,也不包含任何代码实现。
前置知识 :
基础多项式 工业
傅里叶变换(FFT)学习笔记
NTT与多项式全家桶 (不必学完)
理论数学
《具体数学 》
微积分常识
组合数学常识
抽象代数常识
对复杂推导的耐受能力
如果您不理解本文里的某些记号,建议阅读《具体数学》或者高中数学课本。
如果有错漏之处欢迎斧正,但是对于某些明显未编辑完善的部分,就不劳读者费心了。
文末附有数学符号的 \LaTeX 表,以及几类特殊数的表格,可以自行取用。
\begin{aligned}
&\text{We must know----We will know.}\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\text{------ \bf David Hilbert}
\end{aligned}
那么,就让我们开始吧!
Ox01.数学杂项
这些数学知识是多项式(生成函数)分析的重要背景,对这一部分数学体系的熟练能让你更快更全面地理解针对多项式的处理技巧。
但是,在实际应用中,这一部分往往并非关键内容。建议年级较低的读者综合自身的数学基础,适当略读。
多项式基础
约定 : F[n] \big( 或 [x^n]F(x)\big) 为 F(x) 的第 n 项系数,反之亦然。(看懂本文的重要基础)
约定 : 求和的上界若不加说明,绝大多数情况为 ∞ 。
\color{blue}\bf\Delta$ **多项式卷积** : $F(x)*G(x)=\sum\limits_{i=0}\sum\limits_{j=0}F[i]G[j]x^{i+j}
则有(F*G)[n]=\sum\limits_{i=0}^kF[i]G[k-i]
定义次数界\pmod{x^n} ,在次数非负(形式上)且运算均由卷积定义的情况下,可以在运算中途只保留界以内的信息。
\color{blue}\bf\Delta$ **多项式复合** : $(F\circ G)(x)=F(G(x))=\sum\limits_{i=0}F[i]G(x)^i
可以用整体法理解,将 G(x) 代入到 F(x) 中。
经典微积分基础
\color{blue}\bf\Delta$ **求导的线性性** : $\begin{cases}(F(x)+G(x))'=F'(x)+G'(x)\\(c*F(x))'=c*F'(x)\end{cases}
&(C)'=0\quad\text{(其中 C 为与 x 无关的常数)}\\
&(x^k)'=kx^{k-1}\\
&(e^x)'=e^x\\
&(a^x)'=a^x\ln a\\
&(\ln(x))'=\tfrac{1}{x}\\
&(\log_ax)'=\tfrac{1}{x\ln a}\\
&(\sin x)'=\cos x\\
&(\cos x)'=-\sin x\\
\end{aligned}
作用于一元函数上,定义为 \vartheta=x{\rm D} 。其中 {\rm D} 为求导算子。
对生成函数施 \vartheta 便于凑出和下标对应的系数 :
- $\color{blue}\bf\Delta$ **偏导数**
对于多元函数 $F(x,y)$ ,对 $x$ 取偏导相当于将 $y$ (等其他元)看做和 $x$ 无关的量,然后求导。
符号记为 $\dfrac{\partial}{\partial x}$。
- $\color{blue}\bf\Delta$ **乘法法则** : $(F(x)G(x))'=F'(x)G(x)+F(x)G'(x)
\color{blue}\bf\Delta$ **除法法则** : $\left(\dfrac{F(x)}{G(x)}\right)'=\dfrac{F'(x)G(x)-F(x)G'(x)}{G^2(x)}
以上两者都可以根据导数的定义求极限证明。
\color{blue}\bf\Delta$ **莱布尼茨公式** : $\left(\dfrac{{\rm d}}{{\rm d}x}\right)^k(F(x)*G(x))=\sum\limits_{i=0}^k\dbinom{k}{i}\left(\dfrac{{\rm d}}{{\rm d}x}\right)^iF(x)\left(\dfrac{{\rm d}}{{\rm d}x}\right)^{k-i}G(x)
可以根据乘法法则,模仿二项式定理来归纳(理解)。似乎应用较少。
\color{blue}\bf\Delta$ **链式法则** : $\dfrac{{\rm d}}{{\rm d}y}\dfrac{{\rm d}y}{{\rm d}x}=\dfrac{{\rm d}}{{\rm d}x}
在做多项式题目的时候尤其注意,不要认为 \dfrac{{\rm d}}{{\rm d}x} 和 \dfrac{{\rm d}}{{\rm d}F(x)} 等价。
先将变量之间的映射关系图(是个DAG)画出来,偏导数会对路径求和。
例 : 有二元函数(映射) u(x,y),\ v(x,y),\ f(x,y) ,且有 h=f(u,v) 。变量关系图如下所示 :
求 \dfrac{\partial h}{\partial x} 时,查看 x\rightarrow h 的路径,分别有 x\xrightarrow{u(x,y)}u\xrightarrow{f(x,y)}h,\ x\xrightarrow{v(x,y)}u\xrightarrow{f(x,y)}h 两条。
则有 \dfrac{\partial h}{\partial x}=\dfrac{\partial h}{\partial u}\dfrac{\partial u}{\partial x}+\dfrac{\partial h}{\partial v}\dfrac{\partial v}{\partial x} ,其中 \dfrac{\partial h}{\partial u},\dfrac{\partial h}{\partial v} 也可以写成 \dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y} 。
一元链式法则由于变量关系只有一条路径,形式较为简单。
\color{blue}\bf\Delta$ **复合函数求导** $G(F(x))=G'(F(x))F'(x)
和链式法则等价 : G(F(x))\frac{d}{dx}=G(F(x))\frac{d}{dF(x)}\frac{dF(x)}{dx}=G'(F(x))F'(x)
- $\color{blue}\bf\Delta$ **积分的线性性** : $\begin{cases}{\large\intop}\big(F(x)+G(x)\big){\rm d}x={\large\int} F(x){\rm d}x+{\large\int} G(x){\rm d}x\\ {\large\int}\big(cF(x)\big){\rm d}x=c{\large\int} F(x){\rm d}x\end{cases}
\color{blue}\bf\Delta$ **积分中的链式法则** ${\large\int}G'(F(x))F'(x){\rm d}x=G(F(x))+C
逆用求导的链式法则即可。
利用求导的乘法法则 (FG)'=F'G+FG' ,移项并积分得 {\large\int}F'G{\rm d}x=FG-{\large\int}FG'{\rm d}x ,即为分部积分公式。
常见的不定极限有 \dfrac{∞}{∞},∞-∞,0*∞ 等,经过一些变换一般都能变成 \dfrac{0}{0} 形式。
使用条件比较暧昧不清,推荐遇事不决洛了再说,但是不要掉坑里却忘记出来。
可以帮助我们求一些看似不收敛的奇怪式子。见“多项式多点求值”。
设 $F^{(n)}(x)$ 为 $F(x)$ 的 $n$ 阶导数。则有 :
$$F(x)=\sum\limits_{i=0}\dfrac{F^{(i)}(a)}{i!}(x-a)^i$$
从实分析上讲,其实就是把不好求的函数使用多项式来拟合(因为多项式可求导任意次),并且使这个多项式在 a 处模仿这个函数的(许多乃至无穷阶)导数,在模仿了动中之动之后想必十分精确。
从幂级数的角度来讲,可以把余项 的次数弄得很高,在某个次数界下得到“精确”解。应用见下文多项式牛顿迭代。
在 $0$ 处使用泰勒展开,可得 $F(x)=\sum\limits_{i=0}\dfrac{F^{(i)}(a)}{i!}x^i$,这是幂级数的形式。
我们可以借助这类级数,以卷积 的形式定义一些东西。其中最经典的是 \exp x=\sum\limits_{i=0}\dfrac{x^i}{i!} 。
- $\color{blue}\text{结论}$ : 若 $G(F(x))=0
如果我们已经得知 F_*(x) 使得 G(F_*(x))=0\pmod {x^\frac{n}{2}}
则有 \large F(x)=F_*(x)-\frac{G(F_*(x))}{G'(F_*(x))}\pmod{x^n}
可以类比求方程数值解的牛顿迭代记忆 : 作切线并获取与 x 轴的交点。
实战中 G 一般较为简单,可以爆算(手动分析)。
倍增来提高解的次数(界),常数项需要特殊考虑。
$F(x)\bmod {x^n}$ 显然也能作为 $\bmod {x^{n/2}}$ 下的一组解,所以 $F(x)=F_*(x)\pmod {x^\frac{n}{2}}
把多项式 G(F(x)) 在 F_*(x) 处展开,得到 :
G(F(x))=G(F_*(x))+\frac{G'(F_*(x))}{1!}\big(F(x)-F_*(x)\big)+\frac{G''(F_*(x))}{2!}\big(F(x)-F_*(x)\big)^2+\dots
看起来并没有简化问题。但是注意到 F_*(x) 和 F(x) 的后 \frac{n}{2} 项相同,所以 F(x)-F_*(x) 的最低次项至少是 x^{n/2} 。
可知 (F(x)-F_*(x))^2,(F(x)-F_*(x))^3\dots 等的最低次项至少是 x^n 。
上面的运算均是 \pmod{x^n} 意义下的级数,所以这些项都变成 0 了,故得 :
G(F(x))=G(F_*(x))+\frac{G'(F_*(x))}{1!}(F(x)-F_*(x))
下面就是整理的力气活,最终能得到 F(x)=F_*(x)-\frac{G(F_*(x))}{G'(F_*(x))} ,证毕。
附 : 由于 G(F_*(x)) 最低次项至少是 x^{n/2} ,所以分母 G'(F_*(x)) 的精度只需 x^{n/2} 即可。
注 : 分析 G'(F(x)) 时,要注意自由元是 F(x) 而非 x 。
当 G 比较经典时,对 F(x) 使用整体法是可行的。但是 G(x) 中可能出现孤立的 x 或者多项式(与 F(x) 无关)。
此时,处理问题的原则是 : 把孤立的多项式当做常数看待,实际上他们也就是“常多项式”。
如果你纳闷为什么会这样,可以尝试分别定义 G(x),F(x) 然后使用经典的多项式复合来得到式子,你会发现根本办不到。所以 G(F(x)) 总是整体定义的。
边界 : B(0,0)=1 。
递推 :
\begin{aligned}
B(a,b)&=\int_0^1t^a(1-t)^b{\ \rm d}t &(0)
\\&=0-\frac{1}{a+1}\int_0^1t^{a+1}\big[(1-t)^b\big]'{\ \rm d}t &(1)
\\&=\frac{b}{a+1}\int_0^1t^{a+1}(1-t)^{b-1}{\ \rm d}t &(2)
\\&=\frac{b}{a+1}\int_0^1t^{a}(1-t)^{b-1}-t^{a}(1-t)^{b}{\ \rm d}t &(3)
\\&=\frac{b}{a+1}\Big(B(a,b-1)-B(a,b)\Big)&(4)
\end{aligned}
其中 (1) 用到了分部积分法。
解得 B(a,b)=\dfrac{b}{a+b-1}B(a,b-1) 。
显然有 B(a,b)=B(b,a) ,根据上式递推不难得到结论。
有限微积分基础 (+阶乘幂)
考虑经典的微分算子 : {\rm D}f(x)=\lim\limits_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h}
有限微积分则基于差分算子 : \Delta f(x)=f(x+1)-f(x)
我们一般在整函数上施用差分算子 \Delta ,所以 1 已经是最近的“极限”了。
记 \rm E 为平移算子,有 {\rm E}f(x)=f(x+1) ,不难发现有 \Delta =E-1 。
众所周知, {\rm D}(x^m)=mx^{m-1} ,这是经典微积分中的一条可爱且重要的性质。
我们希望 \Delta 算子也能有类似的性质,可是尝试 \Delta(x^3)=(x+1)^3-x^3=3x^2+3x+1 ,并没有什么好的性质。
幸运的是,我们可以找到另一种幂,使其满足类似的性质。
下降幂 : x^{\underline{n}}=\overbrace{x(x-1)(x-2)...(x-n+1)}^{\text{共 n 个因子}}
当 n 为负数的时候,认为次数也是负的,能得到 x^{\underline{-n}}=\dfrac{1}{(x+1)(x+2)...(x+n)}
上升幂 : x^{\overline{n}}=\overbrace{x(x+1)(x+2)...(x+n-1)}^{\text{共 n 个因子}}
当 n 为负数的时候,能得到 x^{\overline{-n}}=\dfrac{1}{(x-1)(x-2)...(x-n)}
这两种幂统称为阶乘幂 。为了对比,有时也称普通幂 x^k 为“方幂”。
下降幂和 \Delta 算子天生一对,看 :
\Delta(x^{\underline m})=(x+1)^{\underline m}-x^{\underline m}=(x+1)x^{\underline{m-1}}-(x-m+1)x^{\underline{m-1}}=mx^{\underline{m-1}}
我们得到了堪与经典微积分媲美的结论。
我们也可以对下降幂进行求和,即有限积分(一般左闭右开)。
类似经典积分的 : \int\!x^k=\frac{x^{k+1}}{k+1} ,我们有 : \sum\limits_{i=0}^{n-1}i^{\underline k}=\dfrac{n^{\underline{k+1}}}{k+1} 。
但注意,经典微积分中 k=-1 时有特例 \int\!\frac{1}{x}=\ln x ,这里也有 \sum\limits_{i=0}^{n-1}i^{\underline{-1}}=\sum\limits_{i=0}^{n-1}\dfrac{1}{i+1}=\sum\limits_{i=1}^{n}\dfrac{1}{i} 。
正是调和级数,其实和 \ln x 也非常相似。
下面我们还会不时涉及阶乘幂,所以在此介绍一些(简单的)小性质。
x^{\underline{a+b}}=x^{\underline{a}}(x-a)^{\underline{b}}
x^{\overline{a+b}}=x^{\overline{a}}(x+a)^{\overline{b}}
比较显然,从定义考虑即可。
x^{\underline{n}}=(-1)^n(-x)^{\overline{n}}
x^{\overline{n}}=(-1)^n(-x)^{\underline{n}}
只考虑前者,后者类似。
(-1)^nx^{\overline n}=\big[-(-x)\big]\big[-(-x+1)\big]\big[-(-x+2\big)]...\big[-(-x+n-1)\big]
\qquad\qquad=x(x-1)(x-2)...(x-n+1)=x^{\underline{n}}
应用 : 自然数 k 次方和问题
先来考虑 k=3 的情况。
我们尝试(人类智慧)用下降幂拼凑通常幂,手玩一阵子之后能得到 x^3=x^{\underline{3}}+3x^{\underline{2}}+x^{\underline{1}}
而下降幂的求和是相当容易的,利用上面导出的基础结论以及求和的线性性,能得到:
\sum\limits_{i=0}^{n-1}x^3=\sum\limits_{i=0}^{n-1}x^{\underline{3}}+3x^{\underline{2}}+x^{\underline{1}}
=\sum\limits_{i=0}^{n-1}x^{\underline{3}}+\sum\limits_{i=0}^{n-1}3x^{\underline{2}}+\sum\limits_{i=0}^{n-1}x^{\underline{1}}=\dfrac{x^{\underline{4}}}{4}+x^{\underline{3}}+\dfrac{x^{\underline{2}}}{2}
这些下降幂已经能够方便地计算了,也可以(麻烦地)展开成通常幂的形式:
=\left(\dfrac{x(x+1)}{2}\right)^2
用人类智慧和草稿纸,我们暂时只能对付这些,当我们了解斯特林数之后,这些工具会更强大。
在经典微积分中有 {\rm D}(uv)=\big({\rm D}u\big)v+u\big({\rm D}v\big) ,有限微积分中则是 :
\Delta\big(u(x)v(x)\big)&=u(x+1)v(x+1)-u(x)v(x)
\\&=\Big(u(x+1)v(x+1)-u(x+1)v(x)\Big)+\Big(u(x+1)v(x)-u(x)v(x)\Big)
\\&=v(x+1)\Delta u(x)+u(x)\Delta v(x)
\end{aligned}
这能用算子描述为 : \Delta(uv)=u\cdot\Delta v+{\rm E}v\cdot\Delta u 。
平移算子 {\rm E} 的出现有那么一点突兀,不过它使这个式子变得正确。
分部积分法则
根据乘法法则,移项并施以不定求和可得 :
\sum u\Delta v=uv-\sum{\rm E}v\cdot\Delta u
例 :
\sum\Big(x2^x\Big)\delta x=x2^x-\sum2^{x+1}\delta x=x2^x-2^{x+1}+C
定界后可得 \sum\limits_{k=0}^{n-1}k2^k=n2^n-2^{n+1}+C ,不难解得 C=2 。
\sum\Bigg(x\dbinom{x+n}{n}\Bigg)\delta x
由组合数性质 : \Delta \dbinom{x+n}{n+1}=\dbinom{x+n}{n} 即 \sum\dbinom{x+n}{n}=\dbinom{x+n}{n+1} 。
\text{原式}&=x\dbinom{x+n}{n+1}-\sum\dbinom{x+n+1}{n+1}\delta x
\\&=x\dbinom{x+n}{n+1}-\dbinom{x+n+1}{n+2}
\end{aligned}
可惜的是,在有限微积分中并没有类似链式法则的形式。
Ox02. 生成函数引入
\begin{aligned}
&\text{A generating function is a device somewhat similar to a bag.}\\
&\text{Instead of carrying many little objects detachedly, which could be embarrassing,} \\
&\text{we put them all in a bag. }\\
&\text{And then, we have only one object to carry, the bag.}\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\text{------} \text{\bf George Polya}
\end{aligned}
“生成函数”是组合对象在度量上的投影。 ——李白天 (\bf E.I. )(应该没引用错吧)
现在我们来讨论整本书中最重要的思想,即生成函数的概念…… ——《具体数学 》
对于一个无穷数列 F ,定义其生成函数 为 :
\sum\limits_{i=0}^∞F[i]x^i=F[0]+F[1]x+F[2]x^2+F[3]x^3...+F[k]x^k...
这样,我们讲数列 的每个数分别附上代数对象 x 的幂,从而得到了一个幂级数 (你也可以暂且理解为多项式)。
比如数列 F=\big<1,1,1,1,1...\big> ,其生成函数为 F(x)=\sum\limits_{i=0}^∞x^i=1+x+x^2+...
你可能注意到我的表述非常小心谨慎,“代数对象”和“未知数”似乎略有区别,所以“幂级数”和“多项式”也并不能完全等同。
实际上,幂级数是一个非常广义的概念,多项式只是幂级数的一个子概念。
只要代数对象 x 存在乘法运算,我们用 x^k 这一记号来表示幂次,就能得到幂级数。这里 x 并不一定要是“数字”,可以是任何奇奇怪怪的东西。
(如果学过抽象代数中的多项式环应该不难理解,或者你至少要了解群的基本知识)
在幂级数中,代数对象 x 是什么“值”,我们并不一定需要关心。
若用作生成函数,则 x 的“值”是完全无意义的。我们只关心数列 F[n] ,而非“函数” F(x) ,“函数值”也没有意义。
因此,在分析生成函数时,往往不需要考虑其收敛性(收敛性只是关于值的不等式性质)。
比如说,对于上面的 F(x) ,观察 :
\begin{alignedat}{2}
F(x)&=1+&x+x^2+x^3+...\\
xF(x)&=&x+x^2+x^3+...
\end{alignedat}
可以发现 F(x)-xF(x)=1 ,解得 F(x)=\dfrac{1}{1-x} 。
熟悉实分析的读者可能马上会指出, F(x) 收敛当且仅当 |x|<1 。但在生成函数中,我们可以忽略收敛性问题。
于是有以下定理(几何级数定理 )成立 :
1+x+x^2+x^3+...=\dfrac{1}{1-x}
一般来说,若式子中含有复杂的(无穷或不定)求和,则不便分析。相对更简洁的形式则被称为封闭形式。
如 1+x+x^2+... 的封闭形式即为 \dfrac{1}{1-x} 。
符号 x 总会带给初学者 “这是个未知数,冥冥中需要有个值” 的错觉,下面我们就尝试用一些更加易于辨识的符号代替 x 。
该问题需要群的基本知识,但较为接近生成函数的本质。
由于洛谷 Blog 无法显示某些符号,请移步 云剪贴板
这个问题比较适合初学者理解。
设 F[n]= 支付 n 元的方案数。(约定有 F[0]=1 ,即什么钱都不支付)
接下来我们来看,在生成函数的领域中,这个问题会以什么形式被解决。
我们用 \langle 1\rangle,\langle 2\rangle,\langle 5\rangle 分别表示三种面值的硬币。
我们定义一种支付方案为一组硬币,若有 a 个 \langle 1\rangle , b 个 \langle 2\rangle , c 个\langle 5\rangle ,则记为 \langle 1\rangle^a\langle 2\rangle^b\langle 5\rangle^c 。
对应的价值则为各个硬币的价值总和。设价值函数为 val ,则 val\big(S=\langle 1\rangle^a\langle 2\rangle^b\langle 5\rangle^c\big)=a+2b+5c 。
定义两种支付方案 S_1,S_2 的乘积 为 : 将两种方案中的硬币一起支付。
则有 \langle 1\rangle^{a_1}\langle 2\rangle^{b_1}\langle 5\rangle^{c_1}\times \langle 1\rangle^{a_2}\langle 2\rangle^{b_2}\langle 5\rangle^{c_2}=\langle 1\rangle^{a_1+a_2}\langle 2\rangle^{b_1+b_2}\langle 5\rangle^{c_1+c_2} ,这符合我们对幂的认识。
大意是说,先支付 a_1 个 \langle 1\rangle ,再支付 a_2 个 \langle 1\rangle ,就有 a_1+a_2 个 \langle 1\rangle ,即 \langle 1\rangle^{a_1+a_2} 。另两种面值类似。
对于价值函数,也有 c(S_1\times S_2)=c(S_1)+c(S_2) 。这是符合生活常识的 : 给出的总钱数等于先后两次给出的钱数之和。
为什么不定义加法表示方案的拼接?因为加法负责表示方案的并列。
不难验证乘法分配律 S_1\times(S_2+S_3)=S_1S_2+S_1S_3 。
意义为 : 先支付 S_1 ,后支付 S_2 或 S_3 ,则最终支付的是 S_1S_2 或 S_1S_3 。
以无穷求和来表示所有可能的支付方式。
首先假设我们只有 1 元硬币,则所有支付方式可记为 :
\begin{aligned}
P_{\{1\}}&=\varnothing+\langle 1\rangle+\langle 1\rangle\langle 1\rangle+\langle 1\rangle\langle 1\rangle\langle 1\rangle+...\\
&=\varnothing+\langle 1\rangle+\langle 1\rangle^2+\langle 1\rangle^3+...
\end{aligned}
这其实就是一个幂级数,严格的记法是 P(\langle 1\rangle) ,因为其中存在对象 \langle 1\rangle 。不过为了简洁,我们偶尔省略括号不写。
接下来加入 2 元硬币,所有支付方式可记为 :
\begin{aligned}
P_{\{1,2\}}&=\varnothing P_{\{1\}}+\langle 2\rangle P_{\{1\}}+\langle 2\rangle\langle 2\rangle P_{\{1\}}+\langle 2\rangle\langle 2\rangle\langle 2\rangle P_{\{1\}}+...\\
&=(\varnothing+\langle 2\rangle+\langle 2\rangle^2+\langle 2\rangle^3+...)P_{\{1\}}
\end{aligned}
最后加入 5 元硬币,类似地有 :
\begin{aligned}
P_{\{1,2,5\}}&=(\varnothing+\langle 5\rangle+\langle 5\rangle^2+\langle 5\rangle^3+...)P_{\{1,2\}}
\end{aligned}
综上,可得:
\begin{aligned}
P_{\{1,2,5\}}
&=(\varnothing+\langle 1\rangle+\langle 1\rangle^2+\langle 1\rangle^3+...)\\
&\times(\varnothing+\langle 2\rangle+\langle 2\rangle^2+\langle 2\rangle^3+...)\\
&\times(\varnothing+\langle 5\rangle+\langle 5\rangle^2+\langle 5\rangle^3+...)
\end{aligned}
注意 P_{\{1,2,5\}}\neq \sum\limits_{k=0}\big(\langle 1\rangle+\langle 2\rangle+\langle 5\rangle\big)^k ,读者可以自己思考原因。(注 : 以不同顺序支付同样的硬币应被视为同种方案,但在该式中并非如此)
利用几何级数定理,则有 P_{\{1,2,5\}}=\dfrac{1}{1-\langle 1\rangle}\dfrac{1}{1-\langle 2\rangle}\dfrac{1}{1-\langle 5\rangle} 。
若我们只关心总面值,则记 z^k 为面值和为 k 的某种方案,有 \langle 1\rangle=z^1,\ \langle 2\rangle=z^2,\ \langle 5\rangle=z^5 。
P_{\{1,2,5\}}(z)=\dfrac{1}{1-z}\dfrac{1}{1-z^2}\dfrac{1}{1-z^5}
------------
- **生成函数分析的整体思路**
生成函数计数的分析过程有两步 : **将问题用生成函数刻画,再利用处理幂级数的技巧得到答案。**
这是贯穿全文的一条重要原则。
生成函数计数的困难正来源于这两步之中。
- 生成函数自身结构非常强大,能很好地刻画并适应浩如烟海的各色组合问题。但在某些特殊问题中则显得笨拙多余,如杨表等精心构造的组合结构。
- 我们得到了生成函数后,可能需要非常复杂的技巧来处理它。在某些问题中通过组合手段处理却相对容易。(或者说简洁的组合手段可能蕴含复杂的代数分析)
> (生成函数)蕴含的初等运算,恐怕并不足够具有洞察力以支持得到通过特殊组合对象得出的结论的水平。
——$\bf E.I.
若你不会刻画问题,学再多分析也无用武之地;若你得到了生成函数,但不会进行处理,那么生成函数的形式本身对解决问题毫无帮助。
Ox03. 一些数列的轻量级推导
在该部分中,主要涉及处理幂级数的技巧,而非刻画问题的技巧。
所以,如果在某处卡住了,可以选择暂时跳过,去后文积累其他方面的知识,万不可像我一样直接弃疗整个模块。
在下文中,我们会见到一系列形形色色的生成函数。
为了得到这些生成函数的系数,我们需要将其变形 成已知系数的幂级数,然后提取系数。
我们现在就来总结一下现在已知系数的若干幂级数。
我们约定 \xrightarrow{\bf G} 表示将数列转化为幂级数 (其实就是OGF啦)。
根据几何级数定理,利用整体法 ,马上可以得到下列封闭形式 :
\big<1,1,1,1,1,1...\big>\quad\xrightarrow{\bf G}\quad\dfrac{1}{1-x}
\big<1,a,a^2,a^3,a^4...\big>\quad\xrightarrow{\bf G}\quad\dfrac{1}{1-ax}
\sum\limits_{i=0}x^{ik}\quad=\quad\dfrac{1}{1-x^k}
\sum\limits_{i=0}c^ix^{ik}\quad=\quad\dfrac{1}{1-cx^k}
在封闭形式之中,我们能够更容易地洞察系数的奥秘(通过将封闭形式变回对应数列)。这也是生成函数技巧的重要作用之一。
进一步地,我们还有如下关于二项式的幂级数 :
\Big<\binom{n}{0},-\binom{n}{1},\binom{n}{2},-\binom{n}{3},...(-1)^n\binom{n}{n}\Big>\quad\xrightarrow{\bf G}\quad(1-x)^n
\big<\binom{n}{0},\binom{n+1}{1},\binom{n+2}{2},...\binom{n+k}{k}...\big>\quad\xrightarrow{\bf G}\quad\dfrac{1}{(1-x)^{n+1}}
这两个幂级数的证明需要(广义)二项式定理,可见下文 “差分与前缀和”。
以上就是我们目前已知的所有提取幂级数系数的“桥梁”,下面我们的所有工作都是将手中的生成函数转化带到这些已知形式上来。
递推式定义 : F[0]=0;\ F[1]=1;\ F[n]=F[n-1]+F[n-2](n>1)
把其写成生成函数 F(x)=\sum\limits_{i=0}^∞F[i]x^i ,目前我们还没有获得的任何有用的结论。
我们考虑利用递推式和适当的错位 ,让 F(x) 表示自己。(常用技巧)
观察 $\quad
\begin{alignedat}{2}
F(x)&=F[0]&+F[1]x&+F[2]x^2+F[3]x^3+...\
xF(x)&=&F[0]x&+F[1]x^2+F[2]x^3+...\
x^2F(x)&=&&+F[0]x^2+F[1]x^3+...\
\end{alignedat}
不难发现,当次数 $\geq 2$ 时,$xF(x),x^2F(x)$ 的系数和恰好为 $F(x)$ 的系数。
但是,当次数 $\leq 1$ 时,存在着“边界误差”,可以手动修正。最终写出的式子为 :
$$F(x)-xF(x)-x^2F(x)=x$$
我们已经用 $F(x)$ 表示了自身,而且利用了定义中的所有信息,能约束得到一个唯一解。
现在来解这个方程,得到封闭形式 :
$$F(x)=\dfrac{x}{1-x-x^2}$$
但是这并不能直接告诉我们有用的东西,比如说幂级数系数。
考虑形如 $\dfrac{1}{1-cx^k}$ 的幂级数,其系数我们在上一节中已经非常熟悉。
我们可以把上式变成若干个形如上式的**和**,先对分母使用因式分解。
解 $1-x-x^2=0$ , 得到 $x_1=\frac{-\sqrt{5}-1}{2},x_2=\frac{\sqrt{5}-1}{2}
F(x)=\dfrac{x}{(x-x_1)(x-x_2)}
我们断言 F 能被表示成两个分式的和,即
F(x)=\dfrac{a}{x-x_1}+\dfrac{b}{x-x_2}
接下来解方程 :
\begin{aligned}
&\dfrac{a}{x-x_1}+\dfrac{b}{x-x_2}=\dfrac{x}{1-x-x^2}\\
\Leftrightarrow\ \ &a(x-x_2)+b(x-x_1)=x\\
\Leftrightarrow\ \ &\begin{cases}a+b=1\\ax_2+bx_1=0\end{cases}
\end{aligned}
最终能解得 a=\frac{5-\sqrt{5}}{10},\ b=\frac{5+\sqrt{5}}{10} 。
现在 F(x)=\frac{a}{x-x_1}+\frac{b}{x-x_2} 中的系数都是已知的了,可以提取系数。
\begin{aligned}
F[n]&=[x^n]\bigg(\dfrac{a}{x-x_1}+\dfrac{b}{x-x_2}\bigg)\\
&=[x^n]\dfrac{-a/x_1}{1-x/x_1}+[x^n]\dfrac{-b/x_2}{1-x/x_2}\\
&=-\Big(a/x_1^{n+1}+b/x_2^{n+1}\Big)
\end{aligned}
将 a,b,x_1,x_2 的真实值回代并整理,能够得到大名鼎鼎的斐波那契数列通项公式。
F[n]=\dfrac{\sqrt{5}}{5}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]
应用 : [数学记录]51nod1236 序列求和 V3
一种快速得到二阶递推式通项公式的方法。(和生成函数并关系不大)
隔壁 MO 的用了都说好。
求解 F[n]=a*F[n-1]+b*F[n-2] 的通项公式,其中 F[0],F[1] 已知。
先不考虑 F[0],F[1] 的约束,不妨假设 F 是一个公比为 q 的等差数列。
则 F[n]=a*F[n-1]+b*F[n-2]\Rightarrow q^2*F[n]+aq*F[n]+b*F[n] 。
即 q^2-aq-b=0 ,解这个方程可以得到两个根 q_0,q_1 。
不难发现,两个满足递推公式的数列的线性组合(和)也必然满足递推公式。
即 : 对于任意 k_0,k_1 , F[n]=k_0q_0^n+k_1q_1^n 都能满足递推公式。
只需根据 F[0],F[1] 的值解出 k_0,k_1 的值即可。
学完可以去做一下 P5320 [BJOI2019]勘破神机,感受老北京特色。
平移 : [x^n]x^tF(x)=F[n-t]
拉伸 : F(x^k)\quad\xleftarrow{\bf G}\quad\big\langle F[0],\overbrace{0,0...}^{\text{k-1个}},F[1],\overbrace{0,0...}^{\text{k-1个}},F[2]...\big\rangle
假设对于数列 F 和递推系数 C ,当 n\geq k 时有 \sum\limits_{i=0}^kC[i]F[n-i]=0 则称 F 满足 ( k 阶 ) 线性常系数递推关系。
比如斐波那契数列,满足 F[n]-F[n-1]-F[n-2]=0 ,这就是一个常系数线性递推。
令 F(x) 为 F[n] 的生成函数。
考虑使用递推式来凑出自己次数达到 k 的部分。
构造 F_t(x)=C[t]x^t\bigg(F(x)-\sum\limits_{i=0}^{k-t-1}F[i]x^i\bigg)
对 F_t(x) 提取 [x^n] 系数,得到 [n\geq k]C[t]F[n-t] ,恰是定义式所需要的。
由 [n\geq k]\sum\limits_{i=0}^kC[i]F[n-i]=0 能得到 \sum\limits_{t=0}^kF_t(x)=0 ,即 \sum\limits_{t=0}^kC[t]x^t\bigg(F(x)-\sum\limits_{i=0}^{k-t-1}F[i]x^i\bigg)=0 。
我们把 F(x) 移到左边,整理可得 \Big(\sum\limits_{t=0}^kC[t]x^t\Big)F(x)=\sum\limits_{t=0}^{k-1}\Big(C[t]x^t\sum\limits_{i=0}^{k-t-1}F[i]x^i\Big)
能够发现左侧出现了一次 C 的生成函数,设为 C(x) 。右侧的余项,次数小于 k ,设为 P(x) 。
则得到 C(x)F(x)=P(x) ,即 F(x)=\dfrac{P(x)}{C(x)} 。
求形如 F(x)=\dfrac{P(x)}{C(x)} 的系数的通项公式。
正宗的分式分解先咕着。
这里也有一个作用类似的代替品。
考虑找出 k,p 使得 C(x)|(1-x^k)^p ,记 A(x)=(1-x^k)^p/C(x) 。
则 F(x)=\dfrac{A(x)P(x)}{(1-x^k)^p} 。A(x)P(x) 和 (1-x^k)^p 的卷积是容易被表示的。
例 : 上文“找零问题”中,最终得到的生成函数为 F(x)=\dfrac{1}{(1-z)(1-z^2)(1-z^5)} ,需要提取其系数。
可以发现 (1-z)(1-z^2)(1-z^5)\big|(1-z^{10})^{3} 。
\begin{aligned}
A(z)&=(1-z^{10})^{3}/(1-z)(1-z^2)(1-z^5)\\
&=z^{22} + z^{21} + 2 z^{20} + 2 z^{19} + 3 z^{18} + 4 z^{17} + 5 z^{16} \\
&+ 6 z^{15} + 7 z^{14} + 8 z^{13} + 7 z^{12} + 8 z^{11}\\
&+ 7 z^{10}+ 8 z^9 + 7 z^8 + 6 z^7 + 5 z^6 \\
&+ 4 z^5 + 3 z^4 + 2 z^3 + 2 z^2 + z + 1
\end{aligned}
然后有 F[n]=[z^n]\dfrac{A(z)}{(1-z^{10})}^3=\sum\limits_{i+j=n}A[i][z^j]\dfrac{1}{{(1-z^{10})}^3}
注意到 [z^n]\dfrac{1}{{(1-z^c)}^k}=[c|n]\dbinom{n/c+k-1}{n/c}
则 F[n]=\sum\limits_{i=0}^{22}A[i]\big[10|(n-i)\big]\dbinom{(n-i)/10+2}{(n-i)/10}
这是有限求和,已经是一个良好的通项公式。
定义 : C[0]=1;\ C[n]=\text{n对括号的合法序列数}(n>1)
首先我们来推导一下递推式.能得到 :
C[n+1]=\sum\limits_{i=0}^{n}C[i]C[n-i]
组合理解 : 枚举第一对括号里面装了多少东西,其内外各为完整的合法序列。
直接依靠这个式子来计算是 O(n^2) 的,我们利用生成函数,看看能不能得到更好的结果。
这个式子看起来非常像卷积,我们令其自卷试试 :
C^2[k]=\sum\limits_{i=0}^kC[i]C[k-i]=C[k+1]
注意, C[k+1] 的幂级数即为 \frac{C(x)-1}{x} (去掉末位然后右移一位)
也就是说 C(x)^2=\frac{C(x)-1}{x} ,解这个方程能够得到 C(x)=\dfrac{1±\sqrt{1-4x}}{2x}
出现了两个根,我们该取那个呢?
按理说 \lim\limits_{x\rightarrow0}C(x)=C[0]=1 才对,我们试试看。
$\lim\limits_{x\rightarrow0}\dfrac{1-\sqrt{1-4x}}{2x}=1$ ,上下是等量无穷小,收敛。
关于多个解的取舍,不需要精细判别,如果数列存在则必然有一根正确。一般情况下,我们只需把显然错误的解舍去即可。
然后根据广义二项式定理 : $\sqrt{1-4x}=\sum\limits_{i=0}^∞\dbinom{1/2}{i}(-4x)^i
事实上这已经给出了系数 : C[k+1]=\dfrac{1+\dbinom{1/2}{k}(-4)^k}{2} 。
将广义二项式系数拆开可以得到更漂亮的式子 : C[k+1]=\dfrac{1}{n+1}\dbinom{2n}{n}
P4931 [MtOI2018]情侣?给我烧了!(加强版)
这是简单版的解法 : Link
里面的式子看起来像卷积,拆开来看看:
\sum\limits_{i=0}^n(-1)^{i}\dbinom{n}{i}^2i!2^i(2(n-i))!
=\sum\limits_{i=0}^n(-1)^{i}\left(\dfrac{n!}{i!(n-i)!}\right)^2i!2^i(2(n-i))!
=(n!)^2\sum\limits_{i=0}^n\dfrac{(2(n-i))!}{(n-i)!^2}\dfrac{(-2)^i}{i!}
这已经是卷积形式了,但是 NTT 跑 5\times10^6 不太行,再推一下生成函数。
设 F(x)=\sum\limits_{i=0}^n\dfrac{(2(n-i))!}{(n-i)!^2}\dfrac{(-2)^i}{i!}x^i
设 G[n]=\dfrac{(2n)!}{n!^2},\ P[n]=\dfrac{(-2)^n}{n!} ,能得到 :
F(x)=G(x)*P(x)
P(x)=\sum\limits_{i=0}\dfrac{(-2x)^i}{i!}=e^{-2x}
G(x)=\sum\limits_{i=0}\dfrac{(2i)!x^i}{i!^2}=\sum\limits_{i=0}\dbinom{2i}{i}x^i=\dfrac{1}{\sqrt{1-4x}}
注 : 关于 \binom{2n}{n} 形的二项式系数可能比较难对付,可见下文“广义二项式定理”。
我们就能得到 F(x)=\dfrac{e^{-2x}}{\sqrt{1-4x}}
对于这种小结构,选择求导并表示自身会有奇效(基本也是唯一的办法?)。
F'(x)=\dfrac{8x*e^{-2x}}{(1-4x)^{3/2}}=\dfrac{8x}{1-4x}F(x)
能够整理为
F'(x)=4xF'(x)+8xF(x)
提取 [x^n] 系数可得
F'[n]=4F'[n-1]+8F[n-1]
(n+1)F[n+1]=4nF[n]+8F[n-1]
注意到我们前面曾经提取出一个 n!^2 ,递推完毕之后乘回来即可。
当然也可以直接考虑到递推式中 :
(n+1)\dfrac{D[n+1]}{(n+1)!^2}=4n\dfrac{D[n]}{n!^2}+8\dfrac{D[n-1]}{(n-1)!^2}
D[n+1]=4n(n+1)D[n]+8n^2(n+1)D[n-1]
根据该式直接递推即可。评测记录
可见 xtq 的知乎回答 : Link
注意到“不会相邻”的限制,考虑容斥。
设 G[n,k]= 长度为 n 的排列中,有恰好 k 处满足相邻差为 1 的方案数,那么 G[n,0] 就是答案。
设 F[n,k]= 长度为 n 的排列中,钦定 k 处满足相邻差为 1 ,其余随意的方案数。
那么由经典容斥(二项式反演)有
G[n,0]=\sum\limits_{i=0}^n(-1)^iF[n,i]
考虑如何计算 F ,我们把满足相邻差为 1 的极长连续段称为块,不难发现 F[n,k] 拥有 n-k 个块。
对于一个块,由于已经固定相邻差为 1 ,容易发现只有顺排,逆排两种。
若块大小只有 1 ,甚至只有一种。
所以,单块的生成函数是
P(x)=x+2x^2+2x^3+2x^4+...=\dfrac{x^2+x}{1-x}
接着考虑拼接 c 个块,形成排列。
我们发现块内“标号”一定是连续的,这就不需要动用 EGF 了。
此时组合意义是有序拼接,直接上 OGF ,拼完之后块间还能任意打乱,故 c!P(x)^c 即为答案。
注意到 F[n,k]=[x^n](n-k)!P(x)^{n-k}
那么若设 H(x)=\sum\limits_{i=0}G[i,0]x^i ,即答案的生成函数。则有
H(x)=\sum\limits_{n=0}x^n\sum\limits_{i=0}^n(-1)^i[x^n](n-i)!P(x)^{n-i}
把 i 给反过来 (变为原来的 n-i )
H(x)=\sum\limits_{n=0}x^n\sum\limits_{i=0}^n(-1)^{n}[x^n]i!(-P(x))^{i}
现在就是要把 (-1)^{n} 想办法藏到后面,这样我们就能使前面需要的 x^n 系数和后面的 [x^n] 提取直接对应。
不难发现,由于提取的是 [x^n] 系数,我们使用 -x 替换 x 就能起到这种效果。
H(x)=\sum\limits_{n=0}x^n\sum\limits_{i=0}^n[x^n]i!(-P(-x))^{i}
现在可以直接对应系数
H(x)=\sum\limits_{i=0}i!(-P(-x))^{i}
将 P(x)=\dfrac{x^2+x}{1-x} 代入化简
H(x)=\sum\limits_{i=0}^ni!\bigg(\dfrac{x-x^2}{1+x}\bigg)^{i}
好的,我们得到了一个更加简洁的形式,但是这还并不能帮助我们非常快速地算出答案来。
为了进一步得到特征,首先使用多项式复合来描述问题。
设 R(x)=\sum\limits_{i=0}i!x^i ,改 设 P(x)=\dfrac{x-x^2}{1+x} 。
那么能得到 H(x)=R(P(x)) 。
一般的多项式复合并没有好的解法,但是此处的 R(x) 比较特殊,考虑使用求导大法 (似乎我也只会这个)
\begin{aligned}
R'(x)&=\sum\limits_{i=0}(i+1)!(i+1)x^i\\
x^2R'(x)&=\sum\limits_{i=2}(i-1)!(i-1)x^{i}=\sum\limits_{i=2}(i!-(i-1)!)x^{i}\\
&=\sum\limits_{i=2}i!x^i-\sum\limits_{i=2}(i-1)!x^{i}\\
&=R(x)-x-1-x(R(x)-1)\\
\end{aligned}
(第二步时提升次数太低可能凑不齐余项,提升次数越高越可能得到解,但是余项可能比较多)
最终能解得 : R'(x)=\dfrac{(1-x)R(x)-1}{x^2}
即 R'(P(x))=\dfrac{\big(1-P(x)\big)R(P(x))-1}{P(x)^2}
则 H'(x)=R(P(x))'=R'(P(x))P'(x)=\dfrac{(1-P(x))H(x)-1}{P(x)^2}P'(x)
将 P(x)=\dfrac{x-x^2}{1+x} 代入,一通爆算 :
P'(x)=\dfrac{-x^2-2x+1}{x^2+2x+1}
H'(x)=\dfrac{-x^2-2x+1}{x^4-2x^3+x^2}\Big(\dfrac{x^2+1}{1+x}H(x)-1\Big)
(x^5-x^4-x^3+x^2)H'(x)=(-x^4-2x^3-2x+1)H(x)+x^3+3x^2+x-1
大力提取系数可得 :
(n-4)H_{n-4}-(n-3)H_{n-3}-(n-2)H_{n-2}+(n-1)H_{n-1}=-H_{n-4}-2H_{n-3}-2H_{n-1}+H_{n}
H_n=(n-3)H_{n-4}-(n-1)H_{n-3}-(n-2)H_{n-2}+(n+1)H_{n-1}
Ox04. 生成函数组合计数初步 + 多项式工业练习
除了帮助我们处理数列,生成函数还能刻画并解决一系列组合问题。现在来介绍几种经典的生成函数。
以下的内容如果需要付诸实践,要先了解一些多项式工业。可见 : NTT与多项式全家桶
若你对这部分的内容已经比较熟悉,可以快进到“组合结构符号化”。
组合对象
定义
组合对象 指满足某一性质的树、图、串等可数的对象。组合对象组成的集合成为组合类 。
对于组合类 \mathcal A ,其中每个对象 a\in {\mathcal A} 都被定义了一个 “大小” |a| ,可能代表节点个数,串长等。
将所有大小为 n 的组合对象记作 {\mathcal A}_n 。
定义计数序列 A[n]=|{\mathcal A}_n| ,即大小为 n 的组合对象的总数目,这通常应是有限的。
我们的任务通常是求出 A[n] 的数值。
约定使用字体 \mathcal{ABCDEFG} 来表示组合类。
例 : 定义 S 为字符集为 \{0,1\} 的字符串集合。定义字符串 s 的大小为其长度。
长度为 n 的 01 串共有 2^n 个,则有 S[n]=2^n 。
笛卡尔积
称 \{(a_1,a_2...a_n)\big|a_1\in A_1,a_2\in A_2,...a_n\in A_n\} 为集合 A_1,A_2...A_n 的笛卡尔积。
记作 A_1\times A_2\times...\times A_n 。
也就是从每个集合中各取一个元素形成有序多元组的集合。
例 :若 A=\{a,b,c\},B=\{1,2\} ,则 A\times B=\{(a,1),(a,1),(b,1),(b,2),(c,2),(c,2)\} 。
小性质 : |A\times B|=|A|\times |B| ,即计数的乘法原理。
计数问题中,往往会使用组合对象的笛卡尔积来定义新的组合对象。
对于两个组合对象 a,b 的组合 (a,b) ,定义 |(a,b)|=|a|+|b| 。
这是非常自然的,比如两个长度为 a,b 的串接起来就得到了一个长度为 a+b 的串。
\rm OGF 全称 \rm ordinary\ generating\ function 。即普通生成函数。
设有数列 F[n] ,则其 OGF 为 F(x)=\sum\limits_{i=0}F[i]x^i 。
这也的确是最朴素的构建幂级数的方法,直接给对应位置的系数附上 x 的幂以区分。
两个 OGF 的乘法正是经典的加法卷积,有:
(F*G)[k]=\sum\limits_{i+j=k}F[i]G[j]
前文已经有六个经典的 OGF ,在这里再额外给出两个 :
\{0,1,\frac{1}{2},\frac{1}{3},\frac{1}{4}\dots\}\xrightarrow{\bf OGF}\ln\frac{1}{1-x}=-\ln(1-x)
\{1,1,\frac{1}{2!},\frac{1}{3!},\frac{1}{4!}\dots\}\xrightarrow{\bf OGF}e^x
接下来介绍组合意义。
若有组合类 \mathcal{A,B} ,且 {\mathcal A∩B}=\varnothing ,令 \mathcal{ C=A+B} ,即不相交集合的并。
由加法原理,有 C[n]=A[n]+B[n] ,即 C(x)=A(x)+B(x) 。
若有组合类 \mathcal{A,B} ,令 \mathcal {D=A\times B} ,即笛卡尔积。
其中 \mathcal D 的每个元素 d 都是一个二元组 (a,b) ,其中 a\in {\mathcal A},\ b\in \mathcal B 。
这正是背包计数 : 大小为 i 的物体和大小为 j 的物体打包成大小为 i+j 的物体。而原来独立的两部分组合的方案数为各自内部的方案数的乘积。
有 D[k]=\sum\limits_{i+j=k}A[i]B[j] ,正是加法卷积。
所以有 \mathcal{D=A\times B}\Rightarrow D(x)=A(x)*B(x) 。
注意到,OGF 的乘法(加法卷积)和计数背包 的转移是同构的。因此,我们其实早在学习 DP 时就已经熟悉了该组合结构的代数形式。
设某种号码由小写英文字母和阿拉伯数字组成,且满足所有数字都出现在字母之后。允许没有英文或数字。
求长度为 n 的号码个数。
设 F[n] 为长度为 n 的纯字母串个数,显然是 26^n ,那么其 OGF 即为 F(x)=\sum\limits_{i=0}26^ix^i=\dfrac{1}{1-26x}
设 G[n] 为长度为 n 的纯数字串个数,为 10^n ,那么其 OGF 即为 G(x)=\sum\limits_{i=0}10^ix^i=\dfrac{1}{1-10x}
设 C[n] 为长度为 n 的合法号码串的个数,即答案。
我们枚举字母的个数,能得到 : C[n]=\sum\limits_{i+j=n}F[i]G[j]
这个式子对应着 OGF 的乘法,我们就能得到 C(x)=F(x)G(x)=\dfrac{1}{(1-26x)(1-10x)} 。
事实上,“所有数字都出现在字母之后”可以看作将字母和数字笛卡尔积产生的二元组顺次写出。
例题② : UVA12298 Super Poker II
题意 : 有一副扑克,对于每一个合数点数都有四种花色的牌。
某些牌已经丢失,求出在剩下的牌中选出花色互不相同的四张,且点数之和为 n 的方案数。
这里的限制是“点数之和”,不难联想到加法卷积(背包)。
每种花色建立一个数列 F[i] 记录点数为 i 的牌的个数。
然后把四个数列进行加法卷积 (实际上就是加速的背包) 就行了。
如果这样说理解不来,考虑一张张“拼接”的过程,或者无序“散列”的过程(笛卡尔积),就对应 OGF 的组合意义。
这题没有取模,但是最大值是 10^{13} 级别的,只需要跑 long double 的 FFT 即可。
复杂度 O(n\log n) 。
枚举使用的骨牌数量 k ,需要“拼接” k 个骨牌,生成函数为 A(x)^k 。
则总方案数为 \sum\limits_{k=0}A(x)^k=\dfrac{1}{1-A(x)} 。
使用求逆即可解决,复杂度为 O(n\log n) 。
比如说,斐波那契数 F[n] 就可以看作骨牌 \{1,2\} 拼接的序列,所以封闭形式为 \frac{1}{1-x-x^2} 。
另一个例子是 P4451 [国家集训队]整数的lqp拆分。
可以视作大小为 n 的骨牌有 Fib[n] 种,则封闭形式为 \dfrac{1}{1-\frac{x}{1-x-x^2}} 。
这明示我们把权值设为次数,捣鼓多项式。
设 F[x] 为权值为 x 的二叉树个数,为了方便令F[0]=1 。
设 G[n]=[n∈C] ,描述了限制。
能写出如下的 `DP` :
$$F[n]=\begin{cases}1&(x=0)\\\sum\limits_{i=1}^nG[i]\sum\limits_{j=1}^{n-i}F[j]F[n-i-j]&(\rm otherwise)\end{cases}$$
下式意义为 : 自己的权值 $i$ ,左右子树的权值 $j,\ n-i-j$ 加起来等于 $n$。
可以观察到卷积 : $F(x)=1+G(x)F(x)^2
解得 F(x)=\dfrac{1±\sqrt{1-4G(x)}}{2G(x)} ,利用 \lim\limits_{x\rightarrow 0}G(x)=0 排除,可知取负号时收敛。
如果按照这个式子计算,我们开根求逆之后,还要再卷一次,很不划算。
上下同乘 1+\sqrt{1-4G} 构成平方差得到 :
剩下的就是多项式开根和求逆了。如果你有不拖模板的精神,直接对这个式子牛顿迭代也是个好选择。
- **例题⑤** :[CF917D Stranger Trees](https://www.luogu.com.cn/problem/CF917D)
问题很像生成树计数,但是矩阵树定理只能求 : 所有生成树的边权乘积。
观察到重边的累计满足背包法则。对于原树的边,赋上边权 $x$ ,反之边权是 $1$.
跑矩阵树,会得到一个多项式,其 $[x^k]$ 系数就是答案。
问题在于,我们需要 $O(n^3)$ 次多项式乘法,即便使用`FFT`复杂度也不低于 $O(n^4\log n)$。
注意到答案多项式的次数不超过 $n$ ,我们可以自己算 $O(n)$ 个点值,然后插值。
具体来讲,令 $x=0...n$ ,多次使用矩阵树定理,分别算所有生成树的边权乘积。
然后把得到的点值使用高斯消元插值即可,复杂度 $O(n^4)$。
- **例题⑥** :[题解 P4389 【付公主的背包】](https://www.luogu.com.cn/blog/command-block/solution-p4389)
首先注意到背包就是 `OGF` 卷积,那么可以 `EXP+Ln` 加速计算。
可以从 $\rm Euler$ 变换(在后面无标号计数中会专题讲解)更加系统的理解。
## $\rm EGF
全称 \rm exponential\ generating\ function 。
设有数列 F[n] ,则其 EGF 为 F(x)=\sum\limits_{i=0}F[i]\dfrac{x^i}{i!} 。
也就是说,在第 i 次项额外除了个 i! 。
能留意到, \{1,1,1,1...\} 的 EGF 就是 \sum\limits_{i=0}\dfrac{x^i}{i!}=e^x ,这也是其名字来源。
两个EGF的乘法为二项 加法卷积,有:
(F*G)[k]=\sum\limits_{i+j=k}\dbinom{k}{i}F[i]G[j]
这不像上次那样显然,我们证明一下。
先把 i! 显示出来,然后就可以当做 OGF 考虑。
\dfrac{(F*G)[k]}{k!}=\sum\limits_{i+j=k}\dfrac{F[i]}{i!}\dfrac{G[j]}{j!}
把阶乘们合并成组合数 :
=\sum\limits_{i+j=k}\dfrac{k!}{i!j!}\dfrac{F[i]}{i!}\dfrac{G[j]}{j!}
由 i+j=k 则有 \dfrac{k!}{i!j!}=\dbinom{k}{i}=\dbinom{k}{j} .
这里也给出一些常用的 EGF :
接下来是组合意义。
仍然有 \mathcal{C=A+B} \Rightarrow C(x)=A(x)+B(x) 。
关于(有/无)标号的概念介绍,详见“图计数”板块。
给定两个有标号对象 a,b ,分别带有 1,2,...,|a| 和 1,2,...,|b| 的标号。
将 a,b 拼接得到 c 时,需要给 c 分配 1\sim |c|=|a|+|b| 的标号。
规定标号分配时, a,b 内部需要保持原有的相对顺序(这样构成双射)。
方案数则为 \dbinom{|a|+|b|}{|a|} ,可以视作选出 |a| 个标号给 a ,其余给 b 。
另一种理解是,将两个部分归并,不同的归并方案数也是上式。
$\rm EGF$ : `{AAAA}×{BBB} → {AABABBA},{BAABAAB},{BBABAAA}...共C(4+3,3)种`
所以,有 $\mathcal{C=A\times B}\Rightarrow C(x)=A(x)=B(x)$。
注意,我们在实战中把 `EGF` 当成 `OGF` 来运算,所以结束时提取系数需要乘以 $i!$ (易被遗忘)。
- **例题①** : 「**染色问题**」(纯数学)
用红蓝绿三种颜色,涂一个长度为 $n$ 的纸条,使得红色和蓝色的个数是偶数,求方案数。
我们用单独一种颜色涂任意长的纸条,方案数都是 $1$ 。由于前两种颜色不能涂奇数个,可以认为奇数的方案数是 $0$ 。
然后,我们给纯色的纸条分配标号,“归并”成多色的纸条,而这对应着 `EGF` 卷积。
绿色的`EGF` : $\sum\limits_{i=0}\dfrac{x^{i}}{i!}=e^x\quad$ ( $\{1,1,1,1...\}$ )
红和蓝的`EGF` : $\sum\limits_{i=0}\dfrac{x^{2i}}{(2i)!}=\dfrac{e^x+e^{-x}}{2}\quad$ ( $\{1,0,1,0...\}$ )
把生成函数乘起来得到:
$$\left(\dfrac{e^x+e^{-x}}{2}\right)^2e^x=\dfrac{e^{3x}+2e^x+e^{-1}}{4}$$
(分别)提取系数就能得到 :
$${\rm Ans[n]}=\dfrac{3^n+2+(-1)^n}{4}$$
- **例题②** : [HDU1521 排列组合](http://acm.hdu.edu.cn/showproblem.php?pid=1521)
有 $n$ 种颜色,每种颜色都有可染的次数,求染一条长度为 $m$ 的纸袋的方案数。
一个可以染最多 $m$ 次的颜色的 `EGF` 是 $\sum\limits_{i=0}^m\dfrac{x^i}{i!}$。
将各个颜色的 `EGF` 卷起来即可得到答案。
数据范围较小,想怎么卷就怎么卷。
- **例题③** :[P5219 无聊的水题 I](https://www.luogu.com.cn/problem/P5219)
**题意** : $n$ 个点且最大点度为 $m$ 的有标号无根树个数。
和度数有关,不难联想到 `prufer` 序列,详细内容可见下文“图计数”。
`prufer` 序列提出了构造 : 长度为 $n-2$ 的任意填写的节点数列,和无根树之间的双射。
点$u$在排列中出现恰好 $(\text{度数}-1)$ 次。
所以,题目就是要我们统计 : 填 $[1,n]$ ,且出现次数最多的数恰好出现了 $m$ 次,长度为 $n-2$ 的数组个数。
“最多恰好”并不好做,我们可以考虑变为“不超过”,然后减去(差分)。
具体来讲,我们统计 $[\leq m-1]$ 的,再统计 $[\leq m]$ 的,然后相减即可。
仿照上一题的思路,我们考虑先得出纯色的 `EGF` ,注意有长度(出现次数)的限制。
$$F(x)=\sum\limits_{i=0}^m\dfrac{x^i}{i!}$$
然后,由于我们有 $n$ 种颜色(节点),我们需要卷积 $n$ 次,再取 $n-2$ 项系数。答案就是:
$$[x^{n-2}]F(x)^n$$
需要多项式快速幂。并不卡常,可以直接倍增快速幂。
复杂度 $O(n\log n)$ 或 $O(n\log^2n)$。 [评测记录](https://www.luogu.com.cn/record/19305774)
- **例题④** : [题解 P5339 【[TJOI2019]唱、跳、rap和篮球】](https://www.luogu.com.cn/blog/command-block/solution-p5339)
二项式反演之后就能转化成排列计数,上 `EGF` 即可。
- $\bf exp$ 的~~惊天大秘密~~**组合意义**
我们观察 $\exp F(x)$ 的展开式 : $\sum\limits_{i=0}\dfrac{F(x)^i}{i!}
这个式子看似平淡无奇,实则暗藏了一个十分优美的组合意义 : 生成集合。
如果把 F(x) 视作“单个元素”的 EGF ,那么 \exp F(x) 就描述了这些元素组成的有标号集合。
展开式的意义是 : 枚举有几个元素,多次卷积拼接,由于元素之间无序需要除以个数的阶乘。
这能够给我们极大的帮助。对于一个集合计数的问题,我们只需要弄清单个元素的特征,就能 \exp 而得到答案。
题意 : 给出一个集合 S ,求环大小在 S 内的 1...n 元置换的个数。
置换其实就是一系列环有标号生成的集合。
一个大小为 n 的环有 (n-1)! 种。因为环能旋转,所以等价类大小总为 n ,用排列总数 n! 除去 n 就得到等价类总数。
考虑单个环的 EGF : \sum\limits_{i=1}[i∈S]\dfrac{(i-1)!x^i}{i!} (注意,只能使用在S 内的环)
然后做一个 \exp 就吼了,是不是非常 excited 啊! 复杂度O(n\log n) 。
事实上,若所有大小的环都可选,则单个环的 EGF 为 \sum\limits_{i=1}\dfrac{(i-1)!x^i}{i!}=-\ln(1-x)
则任意置换的 EGF 为 \exp(-\ln(1-x))=\dfrac{1}{1-x} ,这符合 n 元置换有 n! 个的事实。
例题⑥ : P4841 [集训队作业2013]城市规划
反过来考虑 : 连通图是组成一般图(可联通可不联通)的基本元素。
设连通图的 EGF 为 G(x) ,一般图的 EGF 为 F(x) ,则有 \exp G(x)=F(x) 。
我们现在需要的是 G(x) 而非 F(x) ,可以两边取对数得到 \ln F(x)=G(x) 。
现在只需要得到 F(x) 了。一般图限制很松,是比较好统计的。
考虑 n 个点的带标号无向完全图有 \binom{n}{2} 条边,每一条都可以选或不选,方案数就是 2^{\binom{n}{2}} 。
取 \ln 即可,复杂度是 O(n\log n) 。
例题⑦ : [数学记录]P5162 WD与积木
当元素之间也有序,问题反倒变得简单起来。
一般地,对于一类组合对象 A ,对由 A 种元素组成的序列定义一类新的组合对象 B ,则 B 的生成函数为 :
B(x)=\sum\limits_{i=0}A(x)^i=\dfrac{1}{1-A(x)}
这一结论对于无标号(OGF),有标号(EGF)的情况都成立。
\rm PGF 全称 \rm probabilistic \ generating\ function 。
并不是用于组合对象(集合大小)计数,而是用于概率期望领域。
设 P(\text{表达式}) 为“表达式”为真的概率。
对于一个离散随机变量 X ,约定 X\in N 。
其概率生成函数为 F(z)=\sum\limits_{i=0}P(X=i)z^i
显然有 \sum\limits_{i=0}P(X=i)=1 ,故 F(1)=1 。
还有 E(X)=\sum\limits_{i=0}P(X=i)i=F'(1)
可以进一步扩展到 E(X^{\underline k})=F^{(k)}(1) (就是 k 阶导)
普及一个方差的计算式 : {\rm Var}(X)=E((X-E(X)^2))=E(X^2-2X·E(X)+E(X)^2)=E(X^2)-E(X)^2
尝试使用概率生成函数描述,我们怎么凑出 E(X^2) 呢?
注意到 X^{\underline 2}+X^{\underline 1}=X^2 , 而 E(X^{\underline 2})=F''(1)
F''(1)+F'(1)=\sum\limits_{i=0}i(i-1)P(X=i)+iP(X=i)=\sum\limits_{i=0}i^2P(X=i)=E(x^2)
所以有 {\rm Var}(X)=F'(1)^2-F''(1)-F'(1)
例题① : P4548 [CTSC2006]歌唱王国
设 F[n] 为恰好在第 n 次结束的概率, G[n] 为到了第 n 次仍未结束的概率。
设 F,G 分别为两者的PGF,则 F'(1) 即为答案。
考虑唱一个数,此时要么结束,要么没结束,可以得到如下式子:
F(z)+G(z)=zG(z)+1
比对 [z^n] 系数,左侧即为恰好在 n 次结束以及在 n 之后结束的概率和,即为在 \geq n 轮后结束的概率。
右侧把 G 整体移动了一下,则 [z^n] 系数是原来的 G[n-1] ,也就是在 > n-1 轮,即\geq n 轮后结束的概率。
设该字符串 S 长度为 m ,字符集为 c 。
考虑如何保证 得到一个完整的串,可以直接在未完成的操作序列后面加上该串。
生成函数为 G(z)*\Big(\dfrac{z}{c}\Big)^m 。
这样,虽然保证一定结束了,但是可能早于预期。
我们考虑再使用 F(x) 拼一次同样意义的式子。
我们枚举在加入操作中途何时真正结束,容易发现一定会在某个 \rm Border 处结束,设 A[i]=\big[S[1,i]=S[m-i+1,m]\big]
能得到 $\sum\limits_{i=1}^nA[i]F(z)\Big(\dfrac{z}{c}\Big)^{m-i}
后面的 \Big(\dfrac{z}{c}\Big)^{m-i} 即补全结束后仍然多余的 m-i 个操作,以凑出和前面式子相同的意义。
所以有 :
G(z)*\Big(\dfrac{z}{c}\Big)^m=\sum\limits_{i=1}^mA[i]F(z)\Big(\dfrac{z}{c}\Big)^{m-i}
这种思想其实非常的妙,有点类似容斥。首先确保结束而不考虑多余操作,然后再枚举多余操作得到同样的意义,从而建立 G,F 之间的关系。
这个两个式子的思想非常套路,会反反复复地见到 (
接下来进行分析。
对于 F(z)+G(z)=zG(z)+1 ,两边求导可得 F'(z)+G'(z)=zG'(z)+G(z)
代入 z=1 得 F'(1)+G'(1)=G'(1)+G(1) 即 F'(1)=G(1) ,我们的目标变为了求 G(1) 。
G(1)*\Big(\dfrac{1}{c}\Big)^m=\sum\limits_{i=1}^mA[i]F(1)\Big(\dfrac{1}{c}\Big)^{m-i}
注意到 F(1)=1 并两边同乘 c^m 可得
G(1)=\sum\limits_{i=1}^mA[i]c^{i}
现在可以直接计算了。评测记录
例题② : P3706 [SDOI2017]硬币游戏
不难发现是上一题扩展到多串的情况。
设 G[i] 为第 i 步仍未结束的概率, F_k[i] 为 第 i 步第 k 位同学获胜的概率。
那么类似地有 G(z)+\sum\limits_{i=1}^nF_k(z)=zG(z)+1
接下来,我们通过在现有的序列后面直接加上某个串,来制造必然有某位同学已经胜出的局面。
设加入的是第 k 个串,则有 :
G(z)2^{-m}=\sum\limits_{i=1}^n\sum\limits_{j=1}^mT[k][i][j]F_i(z)2^{-(m-j)}
其中, T[k][j][j]=\big[S_k[1,j]=S_i[m-j+1,m]\big] ,容易使用 hash O(n^3) 求出。
组合意义类似,就是枚举在那个串的那个位置提前结束。
令 z=1 并化简可得:
\sum\limits_{i=1}^nF_k(1)=1
G(1)2^{-m}=\sum\limits_{i=1}^n\sum\limits_{j=1}^mT[k][i][j]F_i(1)2^{-(m-j)}
现在我们有 F_{1...n}(1),G(1) 共 n+1 个未知数,和上述 n+1 个方程,直接高斯消元即可。
没有取模十分奇妙,请注意您的精度。
评测记录
例题③ : HDU4652 Dice
有一个 m 面的均匀骰子。
其实这是 例题② 的一种特殊情况。
在子问题(1)中,匹配集是所有“清一色”串。
在子问题(2)中,匹配集是所有“排列”串。
设 G[i] 为第 i 步仍未结束的概率, G(z) 为其 PGF ,类似地有答案为 G(1) 。
设 F[i] 为 第 i 步结束的概率,F(z) 为其 PGF。
设串总数为 C 。
不难发现所有串都是等价的,所以在特定的某个串结束的 PGF 为 F(z)/C 。
考虑加入某个串 S 来保证停止,同时枚举真正停止的位置和串,可得 :
定义 T[i] 为 : 长为 i 的后缀等于 S 长为 i 的前缀的串数。
G(z)m^{-n}=\sum\limits_{i=1}^nT[i]m^{-(n-j)}F(z)/C
令 z=1 ,注意到 F(1)=1 ,整理得 :
G(1)=\sum\limits_{i=1}^nT[i]m^{j}/C
现在问题只剩求出 T 了。
(1)此时每个串只能和自己匹配,且总能匹配,故 T[i]=1 。
有 C=m ,则答案为 \sum\limits_{i=0}^{n-1}m^i=\dfrac{1-m^n}{1-m}
(2)此时 T[i] 相当于钦定一个长为 i 的后缀,也就是说还有 n-i 个位置可以在剩余的 m-i 个数中任选。
则 T[i]=(m-i)^{\underline{n-i}} 。
有 C=m^{\underline n} ,则答案为
\dfrac{1}{m^{\underline n}}\sum\limits_{i=1}^{n}(m-i)^{\underline{n-i}}m^i=\sum\limits_{i=1}^n\dfrac{m^i}{m^{\underline i}}
本节补充综合练习 :
[数学记录]51nod1514 美妙的序列
[数学记录]P5401 [CTS2019]珍珠 (+二项式反演+求导大法)
[数学记录]P5850 calc加强版
题解 P5860 【「SWTR-03」Counting Trees】 (分式域初涉)
[数学记录]Loj#6503. 「雅礼集训 2018 Day4」Magic
[数学记录]P6516 [QkOI#R1] Quark and Graph
[数学记录]CF923E Perpetual Subtraction
Ox05. 关于二项式
二项式系数在组合问题中非常常见,熟练处理是必要的。
- $\color{blue}\bf(1)$ **拆开组合数**
$$\dbinom{n}{m}=\dfrac{n!}{m!(n-m)!}\qquad\color{blue}$$
考虑这些物品的所有**排列**,我们钦定前 $m$ 个被选出来,构造一种选取方案。
前 $m$ 个或后 $n-m$ 个任意打乱后,还能产生同种选取方案,等价类大小为 $m!(n-m)!$。
等价类个数就是 $\dfrac{n!}{m!(n-m)!}$。又作 $\dbinom{n}{m}=\dfrac{n^{\underline {m}}}{m}$。
这个式子只依靠经典的组合意义,所以只在 $0\leq m\leq n$ 时确保成立。
一些**推论**:
1. **对称性** : $\dbinom{n}{m}=\dbinom{n}{n-m}\qquad\color{blue}
吸收/释放 : \dbinom{n}{m}=\dfrac{n}{m}\dbinom{n-1}{m-1}
可以用来吃掉一些二项式系数旁边的讨厌的数。也可以用于递推。
(x+y)^k=\sum\limits_{i=0}^k\dbinom{k}{i}x^iy^{k-i}
可以考虑拆括号的时候,可以选择乘上 x 或 y ,而选择 i 个 x 的方案数就是\binom{k}{i} 。
注意 1 的幂可能隐藏在求和中。
练习 : CF997C Sky Full of Stars (+二维二项式反演)
\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}
可以考虑组合意义 : 钦定m 个物品中的一个,选到它的方案数是 \binom{n-1}{m-1} ,没选到的方案数是 \binom{n-1}{m} 。
当然也可以直接拆组合数 :
\dbinom{n-1}{m}+\dbinom{n-1}{m-1}=\dfrac{(n-1)!}{m!(n-m-1)!}+\dfrac{(n-1)!}{(m-1)!(n-m)!}
\dfrac{(n-1)!(n-m)+m(n-1)!}{m!(n-m)!}=\dfrac{n!}{m!(n-m)!}=\dbinom{n}{m}
写出帕斯卡三角 有利于理解相关的求和。
一些推论 和技巧 :
平行求和 : \sum\limits_{i=0}^n\dbinom{r+i}{i}=\dbinom{r+n+1}{n}
=\dbinom{r}{0}+\dbinom{r+1}{1}+\dbinom{r+2}{2}+\dots+\dbinom{r+n}{n}
注意到 \binom{r}{0}=1=\binom{r+1}{0} ,可以合并最左端的两个组合数 : \binom{r+1}{0}+\binom{r+1}{1}=\binom{r+2}{1}
接着,又有 \binom{r+2}{1}+\binom{r+2}{2}=\binom{r+3}{2} ,如此归纳即可得到结论。
上指标求和 : \sum\limits_{i=0}^n\dbinom{i}{m}=\dbinom{n+1}{m+1}
注意到 $\binom{m}{m}=1=\binom{m+1}{m+1}$ ,可以合并最左端的两个组合数 : $\binom{m+1}{m+1}+\binom{m+1}{m}=\binom{m+2}{m+1}
接着,又有 \binom{m+2}{m+1}+\binom{m+2}{m}=\binom{m+3}{m+1} ,如此归纳即可得到结论。
还有另一个有趣的组合解释 : 考虑从 0\dots n 中选出 m+1 个数字,则选中的最大数为 i 的方案数为\binom{i}{m} 。
裂项优化DP状态 : 题解 P4707 【重返现世】
裂项以导出递推式 :
题解 P6031 【CF1278F Cards 加强版】
题解 AT2070 【[ARC061D] 3人でカードゲーム / Card Game for Three】
首先显然有 F(x)=(1+x)^{n+m}=(1+x)^n(1+x)^m
按照多项式卷积,把两边的式子提取系数:
F[k]=\dbinom{n+m}{k}=\sum\limits_{i=0}^k\dbinom{n}{i}\dbinom{m}{k-i}
练习 : P2791 幼儿园篮球题 (附送一些二项式推导技巧)
我们需要先定义广义二项式系数 : \dbinom{\alpha}{i}=\dfrac{\alpha^{\underline {i}}}{i!}
好处是,当 \alpha 不是整数的时候,下降幂仍然有定义。(阶乘也可以扩展,不过我们先不动为妙)
(x+y)^{\alpha}=\sum\limits_{i=0}^∞\dbinom{\alpha}{i}x^iy^{k-i}
式子长得差不多,但是现在 \alpha 可以是实数(或者更多?)了。
证明就是考虑 (1+z)^{\alpha} 的麦克劳林级数,多次求导会导致前面的系数变成下降幂的形式 :
(1+z)^{\alpha}\sum\limits_{i=0}\dfrac{\alpha(\alpha-1)...(\alpha-i+1)}{i!}z^i
然后令 z=\frac{x}{y} 再把结果乘以 y^{\alpha} 即可得到一开始的式子。
注意,在数值分析时需要 |z|<1 不然就发散了(一般不被注意……)
普通二项式定理为什么求和到 k 就停下呢? 那是因为之后的组合数都是 0 ,可以弃掉。
广义二项式系数的衍生技巧 :
上指标反转 : 认识和处理上指标为负(整)数的组合数。
可以根据求和公式逆推帕斯卡三角来初步理解。
\dbinom{r}{k}=(-1)^k\dbinom{k-r-1}{k}
考虑 r^{\underline k}=r(r-1)\dots (r-k+1)=(-1)^k(-r)(-r+1)...(k-r-1)=(k-r-1)^{\underline k}
( 熟练的同学会发现 : r^{\underline k}=(-1)^k(-r)^{\overline{k}}=(-1)^k(k-r-1)^{\underline{k}} )
取一半 : 处理 \dbinom{2n}{n} 形组合数。
如果 n 是整数, \dbinom{n-\frac{1}{2}}{k} 能够被(轻易地)写成一些整组合数的乘积。
考虑下降幂的加倍公式 : x^{\underline{k}}(x-\frac{1}{2})^{\underline{k}}=x(x-\frac{1}{2})(x-1)...(x-k+1)(x-k+\frac{1}{2})
=2^{-2k}*2x(2x-1)(2x-2)...(2x-2k+2)(2x-2k+1)=\dfrac{x^{\underline{2k}}}{2^{2k}}
也就是说,我们通过 \frac{1}{2} 让两个下降幂交错,然后乘上 2 的幂,使得间隙扩大为 1 ,变回下降幂。
令 x=k=n ,能得到 : n^{\underline{n}}(n-1/2)^{\underline{n}}=\dfrac{n^{\underline{2n}}}{2^{2n}}
在两边同时除以 n!^2 以产生组合数 : \dbinom{n-1/2}{n}=\dbinom{2n}{n}\Big/2^{2n}
使用上指标反转又可得: \dbinom{-1/2}{n}(-4)^n=\dbinom{2n}{n}
现在我们来大胆地使用上式,尝试得出 \sum\limits_{i=0}\dbinom{2i}{i}x^i 的封闭形式。
=\sum\limits_{i=0}\dbinom{-1/2}{i}(-4x)^i
逆用广义二项式定理。得到 =(1-4x)^{-1/2} ,出人意料的简洁。
当 n 是自然数时,有 :
(x+y)^{\underline{n}}=\sum\limits_{i=0}^n\dbinom{n}{i}x^{\underline i}y^{\underline{n-i}}
(x+y)^{\overline{n}}=\sum\limits_{i=0}^n\dbinom{n}{i}x^{\overline i}y^{\overline{n-i}}
在第一个式子两边除以 n! 并拆开组合数。
\dfrac{(x+y)^{\underline n}}{n!}=\sum\limits_{i=0}^n\dfrac{x^{\underline i}y^{\underline{n-i}}}{i!(n-i)!}
考虑组合数的定义则得到 :
\dbinom{x+y}{n}=\sum\limits_{i=0}^n\dbinom{x}{i}\dbinom{y}{n-i}
正是我们的老朋友,范德蒙德卷积。
对于第二个式子,可以用 x^{\overline k}=(-1)^k(-x)^{\underline k} 来代换即可。
可见 “炫酷反演魔术” ,尤其留意常用结论的 EGF 证法。
n$ 阶差分是 : $\Delta^{n} f(x)=\sum\limits_{i=0}^n\dbinom{n}{i}(-1)^{n-i}f(x+i)
可以用归纳法证明之。
另一种方法是,定义平移算子 $\rm E$ ,使得 ${\rm E}f(x)=f(x+1)
我们的差分算子 \Delta 可以视作 {\rm E}-1 ,因为 \Delta f(x)=f(x+1)-f(x)
我们直接考虑 \Delta^n=({\rm E}-1)^n ,由于算子和括号之间的互动和经典的数字类似,有一个类似的二项式定理成立。
({\rm E}-1)^n=\sum\limits_{i=0}^n\dbinom{n}{k}{\rm E}^k(-1)^{n-k}
我们把 f(x) 乘进去就能得到关于差分的式子。
定义另一个反着的平移算子 {\rm E_{-}} ,使得 {\rm E_{-}}f(x)=f(x-1) ,原来的可写作 \rm E_{+} 。
注意到有 \Sigma f(x)=f(x)+\Sigma f(x-1) ,则 \Sigma=1+{\rm E_{-}}\Sigma ,能解得 \Sigma=\dfrac{1}{1-{\rm E_{-}}}
\Sigma^{n}=(1-{\rm E_{-}})^{-n}=\sum\limits_{i=0}\dbinom{-n}{i}(-{\rm E_{-}})^i
=\sum\limits_{i=0}\dfrac{(-n)^{\underline i}(-1)^i}{i!}({\rm E_{-}})^i=\sum\limits_{i=0}\dfrac{(n+i-1)^{\underline i}}{i!}({\rm E_{-}})^i=\sum\limits_{i=0}\dbinom{n+i-1}{i}({\rm E_{-}})^i
这是数列(多项式系数)的前缀和,而非函数的。
众所周知的是,卷全 1 序列即 \frac{1}{1-x} 可以做前缀和,那么卷 1-x 即做差分。
( 其实,注意到 x 是多项式系数的 {\rm E_{-}} 算子,一切就都解决了 )
差分 : 卷上 (1-x)^k 即可,二项式定理带走。
(1-x)^{k}=\sum\limits_{i=0}\dbinom{k}{i}x^i(-1)^{i}
使用 \dbinom{k}{i}(-1)^{i}=-\dfrac{k-i+1}{i}\dbinom{k}{i-1}(-1)^{i-1} 递推。
前缀和 : 卷上 (1-x)^{-k} 即可,广义二项式定理带走。
(1-x)^{-k}=\sum\limits_{i=0}\dfrac{(-k)^{\underline i}}{i!}x^i(-1)^i=\sum\limits_{i=0}\dfrac{(k+i-1)^{\underline i}}{i!}x^i=\sum\limits_{i=0}\dbinom{k+i-1}{i}x^i
实际上有一些优美的组合意义。
组合数需要使用 \dfrac{(k+i-1)^{\underline i}}{i!}=\dfrac{k+i-1}{i}\dfrac{(k+(i-1)-1)^{\underline {i-1}}}{(i-1)!} 递推。
提交记录
这是一类和数据结构结合的更小巧的问题。这道题可以转化成 : 序列单点修改,维护 m 阶前缀和。
回忆 : \Sigma^{m} F[x]=\sum\limits_{i=0}^x\dbinom{m+i-1}{i}F[x-i]
直接求这个式子并不是好办法。
我们考虑 F[a] 对 \Sigma^{m} F[a+b] 的贡献,为 F[a]\dbinom{m+b-1}{b}
注意, \dbinom{m+b-1}{b} 中, m 是常数,实际上,这是一个关于 \bf b 的 \bf m\!-\!1 次多项式 。 我们不妨将其视作函数h(b) 。
但上面的系数是关于 b (相对距离)的,而非绝对下标。
使用多项式平移的技巧,即从 F(x) 推知 F(x+c) 。
我们可以把 h(x) 变为 h_*(x)=h(x-a) ,这样我们就有 h_*(a+b)=h(b) ,这就转化成了绝对下标。我们能够统一的维护多项式了。
维护多项式(系数)前缀和是容易的,只需每个次数使用一个树状数组维护。得到了多项式之后,代入绝对下标即可。
$$F(x+c)=\sum\limits_{i=0}^m F[i](x+c)^i=\sum\limits_{i=0}^mF[i]\sum\limits_{j=0}^i\dbinom{i}{j}x^jc^{i-j}$$
交换和式可得:
$$=\sum\limits_{j=0}^mx^j\sum\limits_{i=j}^mF[i]\dbinom{i}{j}c^{i-j}$$
所以,$[x^n]F(x+c)=\sum\limits_{i=n}^mF[i]\dbinom{i}{n}c^{i-j}$ ,这就可以 $O(m^2)$ 计算了,后文会提到 $O(m\log m)$ 的方法。
这道题的总复杂度是 $O(nm^2+qm\log n)$ 的。(可以预处理出平移后的每种多项式)
[评测记录](https://www.luogu.com.cn/record/33519836)
- $\color{blue}\bf(9)$ **牛顿级数**
注意到,一个 $m$ 次多项式有很多种表示方式。
可以依照定义表示成朴素的通常幂 : $\sum\limits_{i=0}^mc_ix^k
前面我们也尝试过使用下降幂(的线性组合)来表示多项式,如 \sum\limits_{i=0}^md_ix^{\underline k} 。
这会给我们在某些特殊问题中带来便利(后面大家将会看到更多),但先要确定的是 : 对于任意的多项式,是否总有这种表示呢?
答案是肯定的。注意 x^{\underline m} 是关于 x 的 m 次多项式,我们可以通过取合适的系数,使其消去通常幂的第 m 次项,然后余下的 m-1 次项再用 x^{\underline{m-1}} 对付……以此类推,我们总能消到常数项。
事实上,若 R_i(x) 是关于 x 的 i 次多项式,我们总能在系数合适的时候用 \sum\limits_{i=0}^mc_iR_i(x) 来描述任意多项式。
现在,我们令 R_i(x)=\dbinom{x}{i}=\dfrac{x^{\underline i}}{i!} ,这是符合要求的。
我们就能得到牛顿级数 : F(x)=\sum\limits_{i=0}^mF[i]\dbinom{x}{i}
回忆加法公式,能得到结论 : \Delta_x\dbinom{x}{k}=\dbinom{x}{k-1}
也就是说,牛顿级数的差分(多项式平移)会异常简洁 : \Delta^nF(x)=\sum\limits_{i=n}^mF[i]\dbinom{x}{i-n}
对 F(x)=\sum\limits_{i=0}\dbinom{x}{i}F[i] 使用二项式反演可得 : F[x]=\sum\limits_{i=0}\dbinom{x}{i}(-1)^{m-i}F(i)
众所周知,二项式反演是可以NTT 卷积加速的,所以我们能以 O(n\log n) 的代价做到 : 0...m 点值\Longleftrightarrow 牛顿级数。
可以导出拉格朗日插值的一种特殊情况。
可以用于下文的下降幂多项式。
从牛顿级数可以得出广义二项式定理,不过 OIer 还是不要去管那么多为妙。
从牛顿级数也可以得到泰勒级数的离散模拟,感觉 OI 中没什么用就不写了……
将杨辉三角(可以看作二维数组)写成二元生成函数的形式 :
\begin{aligned}
G[n,m]&=\dbinom{n}{m}\\
G(x,y)&=\sum\limits_{i=0}\sum\limits_{j=0}\dbinom{i}{j}x^iy^j\\
&=\sum\limits_{i=0}x^i(y+1)^i\\
&=\dfrac{1}{1-x-xy}
\end{aligned}
这个简洁的封闭形式将整个杨辉三角蕴含其中。
如果将 y 替换为关于 x 的式子,或将 x 替换为关于 y 的式子,从二元变成一元, x^ay^b 的系数会根据某些条件合并。
例如,令 y=x^k ,则 [x^n]G(x,x^k)=[x^n]\sum\limits_{i=0}\sum\limits_{j=0}\dbinom{i}{j}x^ix^{jk}=\sum\limits_{i+j\times k=n}\dbinom{i}{j} 。
令 x=y^k ,则 [x^n]G(y^k,y)=[x^n]\sum\limits_{i=0}\sum\limits_{j=0}\dbinom{i}{j}x^{ik}x^j=\sum\limits_{i\times k+j=n}\dbinom{i}{j} 。
这是杨辉三角上某个奇怪方向的求和。同时,考察封闭形式即可得到系数。
下面来看更多的求和 :
\sum\limits_{i=0}^m\dbinom{m}{i}
即为 \sum\limits_{i+j\times 0=m}\dbinom{i}{j} ,所以令 y=x^0 得到 G(x,1)=\dfrac{1}{1-2x} 。
提取系数得 \sum\limits_{i=0}^m\dbinom{m}{i}=[x^m]\dfrac{1}{1-2x}=2^m 。
\sum\limits_{i=0}^m\dbinom{i+m}{2i}
注意到 i+m-(2i)/2=m ,故上式即为 \sum\limits_{i-j/2=m}\dbinom{i}{j} 。
令 y=x^{-1/2} 得 G(x,x^{-1/2})=\dfrac{1}{1-\sqrt{x}-x}
则 \sum\limits_{i=0}^m\dbinom{i+m}{2i}=[x^m]\dfrac{1}{1-\sqrt{x}-x}=[z^{2m}]\dfrac{1}{1-z-z^2}=F_{2m+1}
其中 \frac{1}{1-z-z^2} 正是斐波那契数列的生成函数除去一个 z 。
Ox06.其他特殊数
斯特林数
第一类斯特林数 : \begin{bmatrix}n \\ m\end{bmatrix}
(环可以旋转,旋转后相同的算同一个环)
**递推公式**: $\begin{bmatrix}n \\ m\end{bmatrix}=\begin{bmatrix}n-1 \\ m-1\end{bmatrix}+(n-1) \begin{bmatrix}n-1 \\ m\end{bmatrix}
解释 : 考虑新加进来的元素单独成环,方案数为 \begin{bmatrix}n-1 \\ m-1\end{bmatrix} 。
否则需要插入某个环内。对于每个环,有(该环大小)个插入点。所有环的大小和为 n-1 ,所以总的插入点就是 n-1 个。
这部分方案数是 (n-1)\begin{bmatrix}n-1 \\ m\end{bmatrix} 。
\color{blue}\text{一些恒等式:}
1. \sum\limits_{i=1}^n\begin{bmatrix}n \\ i\end{bmatrix}=n!
解释 :一个置换会有若干个循环节, i 个循环节的置换总量刚好对应 \begin{bmatrix}n \\ i\end{bmatrix} 。
所以加起来就不重不漏的统计了所有置换,总数就是 n! 。
也可以理解为下一条的特殊情况。
2. x^{\overline n}=\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i
证明的话先用归纳法:
x^{\overline{n+1}}=(x+n)x^{\overline{n}}=(x+n)\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i
=x\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i+n\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i=\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^{i+1}+n\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i
=\sum\limits_{i=1}^n \begin{bmatrix}n\\i-1 \end{bmatrix}x^{i+1}+n\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}x^i=\sum\limits_{i=1}^n \left(\begin{bmatrix}n\\i-1 \end{bmatrix}+n\begin{bmatrix}n\\i \end{bmatrix}\right)x^{i}
=\sum\limits_{i=1}^n \begin{bmatrix}n+1\\i \end{bmatrix}x^{i}
其实,上升幂的展开方式正是第一类斯特林数递推式的体现。
又能得到 : 幂级数 x^{\overline{n}} 的各项系数就是一行第一类斯特林数。
3. x^{\underline n}=\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}(-1)^{n-i}x^i
如果你学过二项式反演的话,你会发现这个式子有点眼熟,其实这个式子真的和斯特林反演有某些关系哟。
证明的话当然可以再次归纳,不过有一个更好的办法。
x^{\underline n}=(-1)^n(-x)^{\overline n}=(-1)^n\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}(-x)^i=\sum\limits_{i=0}^n \begin{bmatrix}n\\i \end{bmatrix}(-1)^{n-i}x^i
3. S_1(x,y)=\sum\limits_{i=0}\sum\limits_{j=0}\begin{bmatrix}i\\j \end{bmatrix}\dfrac{x^iy^j}{i!}=(1-x)^{-y}
这指出了第一类斯特林数的二元生成函数。
证明 : 一个环排列的 EGF 为 F(x)=\sum\limits_{i=0}\begin{bmatrix}i\\1 \end{bmatrix}\dfrac{x^i}{i!}=\sum\limits_{i=0}\dfrac{x^i}{i}=-\ln(1-x) 。
现在要把圆排列组合成置换,由于用 y 的次数来记录环的个数,单个环排列的生成函数变为 yF(x) 。
置换的生成函数即为 \exp\big(yF(x)\big)=\exp\big(-y\ln(1-x)\big)=(1-x)^{-y} 。
通过这个式子,可以很容易地得到一行第一类斯特林数的 OGF :
n^{-y}
=n![x^n]\sum\limits_{i=0}\dbinom{-y}{i}(-x)^i
=n!(-1)^n\dbinom{-y}{n}=(-1)^n(-y)^{\underline n}=y^{\overline n}
其实就是 k 个环排列组合在一起。
则有 \sum\limits_{i=0}\begin{bmatrix}i\\k \end{bmatrix}\dfrac{x^i}{i!}=\frac{1}{k!}F(x)^k=\dfrac{\big(-\ln(1-x)\big)^k}{k!}
也可以通过上面的二元 GF 得到
\begin{aligned}
&[y^n](1-x)^{-y}\\
=&[y^n]\exp (-y\ln(1-x))\\
=&[y^n]\sum\limits_{i=0}\dfrac{y^i\big(-\ln(1-x)\big)^i}{i!}\\
=&\dfrac{\big(-\ln(1-x)\big)^k}{k!}\\
\end{aligned}
第二类斯特林数 : \begin{Bmatrix}n \\ m\end{Bmatrix}
**递推公式**: $\begin{Bmatrix}n \\ m\end{Bmatrix}=\begin{Bmatrix}n-1 \\ m-1\end{Bmatrix}+m \begin{Bmatrix}n-1 \\ m\end{Bmatrix}
解释 : 考虑新加进来的元素单独成盒,方案数为 \begin{Bmatrix}n-1 \\ m-1\end{Bmatrix}
否则可以随便丢进一个盒子,方案数是 m\begin{Bmatrix}n-1 \\ m\end{Bmatrix} 。
\color{blue}\text{一些恒等式:}
1. m^n=\sum\limits_{i=0}^m\begin{Bmatrix}n \\ i\end{Bmatrix}*i!*\dbinom{m}{i}
解释 : 考虑组合意义。
我们从 $m$ 个盒子里面选出 $i$ 个非空盒子,要乘上$\binom{m}{i}$,
然后把 $n$ 个球放进去,再乘上 $\begin{Bmatrix}n \\ i\end{Bmatrix}$,
然后由于这里盒子不同,最后乘上 $i!$ 。
也可以写作 $x^n=\sum\limits_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}*x^{\underline{i}}
推论 : \sum\limits_{i=0}^ni^k=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1} (设0^0=1 )
左边 =\sum\limits_{i=0}^n\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{i}{j}
=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\sum\limits_{i=0}^n\dbinom{i}{j}
根据上指标求和 :\sum\limits_{i=0}^n\dbinom{i}{j}=\dbinom{n+1}{j+1}
=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1}
例题 : (常用来对付自然数幂)
2. \begin{Bmatrix}n \\ m\end{Bmatrix}=\frac{1}{m!}\sum\limits_{i=0}^m(-1)^{m-i}\dbinom{m}{i}i^n
看起来很复杂? 对1 中式子采用二项式反演即可。
3. \sum\limits_{i=k}\begin{Bmatrix}i \\ k\end{Bmatrix}\dfrac{x^i}{i!}=\frac{1}{k!}(e^x-1)^k
这指出了一列第二类斯特林数的 EGF 。
可以考虑组合意义,单个“盒子”的生成函数是 e^x-1 ,那么 k 个盒子的无序组合就是 \frac{1}{k!}(e^x-1)^k 。
同样可以写成二元 \rm GF : S_2(x,y)=\sum\limits_{i=0}\sum\limits_{j=0}\begin{Bmatrix}i \\ j\end{Bmatrix}\dfrac{x^iy^j}{i!}=\exp\big(y(e^x-1)\big)
证明 : 考虑组合意义,将多个盒子生成无序集合。引入的 y 用于标记盒子数目。
可以用于得到结论2 :
\begin{aligned}
&n![x^n]\exp\big(y(e^x-1)\big)\\
=&n![x^n]\sum\limits_{k=0}\dfrac{y^k(e^x-1)^k}{k!}\\
=&n![x^n]\sum\limits_{k=0}\dfrac{y^k}{k!}\sum\limits_{i=0}^k\dbinom{k}{i}e^{ix}(-1)^{k-i}\\
=&\sum\limits_{k=0}\dfrac{y^k}{k!}\sum\limits_{i=0}^k\dbinom{k}{i}i^n(-1)^{k-i}\\
\end{aligned}
再提取 [y^k] 系数即可。
你可以在 斯特林数的四种求法 中了解到相关的多项式工业。 (贝尓数也在里面)
根据定义分析组合意义(并求和/卷积)的题目 :
根据恒等式,推导出卷积的题目 :
首先需要了解 基本反演推论。
先给出式子:
F[n]=\sum\limits_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}G[i]\Longleftrightarrow G[n]=\sum\limits_{i=0}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}F[i]
设 F,G 的 EGF 为 F(x),G(x) 。则有 :
\begin{aligned}
F(x)&=\sum\limits_{k=0}\dfrac{F[k]x^k}{k!}\\
&=\sum\limits_{k=0}\dfrac{x^k}{k!}\sum\limits_{i=0}\begin{Bmatrix}k \\ i\end{Bmatrix}G[i]\\
&=\sum\limits_{i=0}G[i]\sum\limits_{k=0}\begin{Bmatrix}k \\ i\end{Bmatrix}\dfrac{x^k}{k!}\\
&=\sum\limits_{i=0}G[i]\dfrac{(e^x-1)^i}{i!}\\
&=G(e^x-1)
\end{aligned}
其中倒数第二步使用了一列第二类斯特林数的 EGF 来替换。
略作代换可得 F(\ln(1+x))=G(x) 。
展开可得 :
\begin{aligned}
F(\ln(1+x))&=\sum\limits_{k=0}F[k]\dfrac{\ln(1+x)^k}{k!}\\
&=\sum\limits_{k=0}F[k]\dfrac{(-1)^k\ln(1-(-x))^k}{k!}\\
&=\sum\limits_{k=0}F[k](-1)^k\sum\limits_{i=0}\begin{bmatrix}k \\ i\end{bmatrix}\dfrac{(-x)^i}{i!}\\
&=\sum\limits_{i=0}\dfrac{x^i}{i!}\sum\limits_{k=0}(-1)^{k-i}\begin{bmatrix}k \\ i\end{bmatrix}F[k]\\
\end{aligned}
其中第三步需要对比一列第一类斯特林数的 EGF : \dfrac{(-\ln(1-x))^k}{k!}
对比系数即得到 G[n]=\sum\limits_{i=0}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}F[i]
另外几个形式:
F(n)=\sum\limits_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}G(i)\Leftrightarrow G(n)=\sum\limits_{i=0}^n\begin{bmatrix}n \\ i\end{bmatrix}F(i)
F(n)=\sum\limits_{i=n}\begin{Bmatrix}i \\ n\end{Bmatrix}G(i)\Leftrightarrow G(n)=\sum\limits_{i=n}(-1)^{i-n}\begin{bmatrix}i \\ n\end{bmatrix}F(i)
F(n)=\sum\limits_{i=n}(-1)^{i-n}\begin{Bmatrix}i \\ n\end{Bmatrix}G(i)\Leftrightarrow G(n)=\sum\limits_{i=n}\begin{bmatrix}i \\ n\end{bmatrix}F(i)
都可以根据几个基本反演推论得到。反演的具体应用见 炫酷反演魔术。
利用两类斯特林数,可以在阶乘幂和通常幂之间转换。
x^n=\sum\limits_{k=1}^n\begin{Bmatrix}n \\ k\end{Bmatrix}x^{\underline k}=\sum\limits_{k=1}^n\begin{Bmatrix}n \\ k\end{Bmatrix}(-1)^{n-k}x^{\overline k}
x^{\underline n}=\sum\limits_{k=1}^n\begin{bmatrix}n \\ k\end{bmatrix}(-1)^{n-k}x^k\qquad\quad x^{\overline n}=\sum\limits_{k=1}^n\begin{bmatrix}n \\ k\end{bmatrix}x^k
怎么记忆这三个式子呢? (顺便可以把斯特林反演一起记住)
注意到通常有 x^{\overline n}\geq x^n\geq x^{\underline n} ,我们在用大幂表示小幂的时候,必须附带 (-1)^{n-k} 。
假如我们承认 \begin{bmatrix}0 \\ k\end{bmatrix}=\begin{Bmatrix}0 \\ k\end{Bmatrix}=[k=0] ,且 \begin{bmatrix}n \\ 0\end{bmatrix}=\begin{Bmatrix}n \\ 0\end{Bmatrix}=[n=0] 。(符合常识)
然后,使用递推公式倒推出参数为负数的第二类斯特林数。(可见函数表 )
我们会吃惊地发现,有 \begin{Bmatrix}-k \\ -n\end{Bmatrix}=\begin{bmatrix}n \\ k\end{bmatrix} 成立。
除了暗示我们一行第一类斯特林数和一列第二类斯特林数有类似的求解方法,似乎也没有什么特别的功能。
伯努利数
可能与经典的伯努利数有所出入,但个人认为更加简洁实用,大佬轻喷。
我们现在要对自然数幂和 的多项式进行研究。
我们知道 \{1,c,c^2,c^3...\} 的 EGF 为 G_c(x)=\sum\limits_{i=1}\dfrac{{(cx)}^i}{i!}=e^{cx} ,可以从这里出发进行构造。
如果我们想知道自然数幂和的 EGF ,就需要对 G_c 求和 :
S_n(x)=\sum\limits_{c=0}^{n-1}G_c(x)=\sum\limits_{c=0}^{n-1}e^{cx}=\dfrac{e^{nx}-1}{e^x-1}
这样, S_n(x)=\sum\limits_{k=1}\dfrac{(\sum\limits_{c=0}^{n-1}{c^k})x^k}{k!} ,即 S_n[k]=\dfrac{1}{k!}\sum\limits_{i=0}^{n-1}i^k 。
我们分离出 B(x)=\dfrac{x}{e^{x}-1} (这就是伯努利数的 EGF )
然后可得 S_n(x)=B(x)\dfrac{e^{nx}-1}{x}
把这个卷积拆一下 :
设 G(x)=\dfrac{e^{nx}-1}{x}=\sum\limits_{i=0}\dfrac{n^{i+1}x^i}{(i+1)!} (容易提取系数)
\sum\limits_{i=0}^{n-1}i^k=k!S_n[k]=k!\sum\limits_{i+j=k}G[i]B[j]=k!\sum\limits_{i=0}^{k}\dfrac{B[k-i]n^{i+1}}{(i+1)!}
这就得到了自然数幂和关于 n 的多项式。(用二元GF理解可能更加直观)
**例题** :
- [[数学记录]P3711 仓鼠的数学题](https://www.luogu.com.cn/blog/command-block/post-shuo-xue-ji-lu-p3711)
- [[数论记录]P4464 [国家集训队]JZPKIL](https://www.luogu.com.cn/blog/command-block/post-shuo-lun-ji-lu-p4464-guo-jia-ji-xun-dui-jzpkil) (+数论)
- [[数学记录]P7102 [w3R1] 算](https://www.luogu.com.cn/blog/command-block/post-shuo-xue-ji-lu-p7102-w3r1-suan) (+数论+CZT变换)
## 欧拉数
用处并不像前两种数那样广泛,但仍然能得到一些有趣的结论。可以视作综合练习。
$\color{blue}\text{定义:}$ $\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle=$ 有 $k$ 个升高的,长度为 $n$ 的排列的个数。
其中“升高”定义为让 $p_i<p_{i+1}$ 成立的 $(p_i,p_{i+1})$。
同样有一个比较简洁的递推式 :
$$\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle=(k+1)\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle+(n-k)\left\langle\begin{matrix}n-1\\k-1\end{matrix}\right\rangle$$
对于排列计数问题,我们通常以某种顺序插入元素来得到递推式。在这里我们每次插入更大的数。
假设我们已经有一个 $\{1...n-1\}$ 的排列,需要向其中插入 $n$ ,考虑会如何产生升高。
如果 $n$ 插在一个升高 $(p_i,p_{i+1})$ 的中间,那么 $(p_i,n)$ 会形成一组新升高,而 $(p_{i+1},n)$ 则一定不会产生。升高的总数不变。
如果 $n$ 插在开头,升高的总数也不变。
如果 $n$ 插在其他地方,比如非升高的位置或者末尾,都会产生一个新的升高。
开头和升高之间,共有 $k+1$ 个位置,而总共能够插入的位置是 $n+1$ 个,余下 $n-k$ 个。
- [P5825 排列计数](https://www.luogu.com.cn/problem/P5825)
题意就是快速求出一行欧拉数。
直接手撕递推式比较困难,固然可以选择丢结论并归纳,~~但考场上是不可能有小鸟告诉你答案的~~。
考虑 `OIer` 计数的一般套路 : 把“恰好”反演掉。虽然不显得优美,但是很套路很简洁。
先钦定 $k$ 个上升,其他的地方随便填(仍然可以上升)。
设 $f(k)$ 为上述方案数,考虑怎么计算。
并没有什么直观的组合意义。我们转而考虑特殊情况 : 已经钦定好升高位置之后,填涂方案数是多少。
我们把相邻的上升并在一起,因为由小于号串起来的区间只能有一种排列方式。(而非$u!$种)
如果我们得到的“块”大小的集合是 $S$ ,方案数就是 $\dfrac{n!}{\prod_{u∈S}u!}$。
注意到,我们对原来孤立的 $n$ 个块,合并了 $k$ 次,所以总能得到 $n-k$ 个块。
考虑单个块的贡献,不难发现是大小的阶乘的倒数。
这就能写出单个块的生成函数 : $B(x)=\sum\limits_{i=1}\dfrac{x^i}{i!}=e^x-1$ (大小为 $0$ 的块不应存在)
我们要得到 $m$ 个块,计算 $B(x)^m=(e^x-1)^m$ 即可。
我们实际需要的是块大小和为 $n$ 的贡献和,所以欲求 $[x^n](e^x-1)^m
=[x^n]\sum\limits_{i=0}^m\dbinom{m}{i}e^{ix}(-1)^{m-i}
含有 x 的项只有 e^{ix} ,可以直接对其提取系数。
=\sum\limits_{i=0}^m\dbinom{m}{i}\dfrac{i^n}{n!}(-1)^{m-i}
拆开组合数整理就能得到卷积。
=\sum\limits_{i=0}^m\dfrac{m!}{(m-i)!i!}\dfrac{i^n}{n!}(-1)^{m-i}
=\dfrac{m!}{n!}\sum\limits_{i=0}^m\dfrac{i^n}{i!}\dfrac{(-1)^{m-i}}{(m-i)!}
考虑到这本来就是 EGF ,前面的 \dfrac{1}{n!} 可以不计。
注意,我们现在得到的下标是“块数”,还需要翻转之后才是“上升数”。
现在我们已经得到了 f(0...n) ,来考虑反演。
设 g(k) 为恰有 k 个升高的排列个数。 (即答案)
对于一个有 i 个升高的排列,总有\dbinom{i}{k} 种方案钦定出其中的 k 个升高,于是有如下式子:
f(k)=\sum\limits_{i=k}\dbinom{i}{k}g(i)
二项式反演可得 :
g(k)=\sum\limits_{i=k}(-1)^{i-k}\dbinom{i}{k}f(i)
两次卷积。
将上文计算欧拉数的过程全部展开,可得 :
\begin{aligned}
\left\langle\begin{matrix}n \\ k\end{matrix}\right\rangle&=n!\sum\limits_{i=k}^n\dbinom{i}{k}(-1)^{i-k}[x^n](e^x-1)^{n-i}\\
&=n!\sum\limits_{i=k}^n\dbinom{i}{k}(-1)^{i-k}\sum\limits_{j=0}^{n-i}\dbinom{n-i}{j}(-1)^{n-i-j}[x^n]e^{xj}\\
&=n!\sum\limits_{i=k}^n\dbinom{i}{k}(-1)^{i-k}\sum\limits_{j=0}^{n-k}\dbinom{n-i}{j}(-1)^{n-i-j}\dfrac{j^n}{n!}\\
&=\sum\limits_{j=0}^{n-k}(-1)^{n-k-j}j^n\sum\limits_{i=k}^n\dbinom{i}{k}\dbinom{n-i}{j}\\
&=\sum\limits_{j=0}^{n-k}(-1)^{n-k-j}j^n\dbinom{n+1}{k+j+1}\\
\end{aligned}
最后一步需要注意到 \dbinom{i}{k}=[x^{i-k}]\dfrac{1}{(1-x)^{k+1}},\dbinom{n-i}{j}[x^{n-i-j}]\dfrac{1}{(1-x)^{k+1}} ,于是卷积后即为 [x^{n-j-k}]\dfrac{1}{(1-x)^{k+j+2}}=\dbinom{n+1}{i+j+1} 。
可以一次差卷积计算。
提交记录
欧拉数还满足如下恒等式 :
x^n=\sum\limits_{k=0}^n\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle\dbinom{x+k}{n}
由于对组合数施 \Delta_x 得到的形式很简洁,我们就能导出一些其他有趣的结论。似乎目前没啥有趣的应用,就不讲了。
欧拉数的二元生成函数为 :
E(x,y)=\sum\limits_{n=0}\sum\limits_{m=0}\left\langle\begin{matrix}n \\ m\end{matrix}\right\rangle\dfrac{x^ny^m}{n!}=\dfrac{1-y}{e^{x(y-1)}-y}
分拆数
偶尔也作“拆分数”。
定义 : 记 P_n 为将 n 拆分成若干无序正整数的和的方案数。
如 3 可以拆分成 1+1+1 或 1+2 (和 2+1 视为同种方案)或 3 。于是 P_3=3 。
分拆数的 OGF 为 :
P(x)=\prod_{k=1}\sum_{i=0}x^{ik}=\prod_{k=1}\dfrac{1}{1-x^k}
这个式子的意义是,先枚举拆分的数 k ,再枚举拆分的次数 i 。
由于按顺序从小到大枚举 k ,拆出来的数列是递增的,于是不会重复计数。
根据后文的知识也可以理解为 {\rm MSET}(\rm Z^{+}) ,其中 \rm Z^{+} 是正整数集。
计算方法和 {\rm MSET:Exp} 是一致的,先取 \ln ,再 \rm exp 。
\begin{aligned}
&\prod_{k=1}\dfrac{1}{1-x^k}\\
=&\exp\sum_{k=1}\ln\dfrac{1}{1-x^k}\\
=&\exp\sum_{k=1}\sum_{i=1}\dfrac{x^{ik}}{i}\\
\end{aligned}
后面的求和可以 O(n\log n) 完成。
不难发现,可以用类似完全背包的 DP 来计算分拆数,但复杂度是 O(n^2) 的,无法通过。
考虑根号分治,记 m=\sqrt{n} 。当使用 k 进行拆分时 :
$g[i][j]$ 表示用了 $i$ 个 ( $\geq\!m$ 的数 ),和为 $j$ 的方案数。
边界为 $g[0][0]=1$ ,转移为 $g[i][j]=g[i-1][j-m]+g[i][j-i]
其中前者 g[i-1][j-m] 表示加入一个 m ,后者表示将现在的整个序列整体 +1 。
不难发现这样生成的一定是有序序列,且每种序列生成方法唯一。
不难发现第一维不超过 O(n/m)=O(\sqrt{n}) 。
于是,我们用 O(n\sqrt{n}) 的复杂度算出了 F,G ,然后卷积即可得到分拆数。本题中只需要一个系数,故可线性求得。
实际上,有更强力的方法可以不利用快速多项式乘法在 O(n\sqrt{n}) 内求出 1\sim n 的各个拆分数。
观察 OGF 分母的展开式 :
\prod_{i=1}(1-x^i)=1-x-x^2+x^5+x^7-x^{12}-x^{15}+\dots
发现展开式中大部分项的系数都为 0 ,只有少部分项有 \pm 1 的系数。
经过合理的猜测能够发现 :
\prod_{i=1}(1-x^i)=1+\sum\limits_{i=1}(-1)^ix^{i(3i\pm 1)/2}
其中数 i(3i\pm 1)/2 被称为广义五边形数,这条等式被称为五边形数定理 。
具体证明较为复杂(据说当年欧拉发现结论后也延后了 10 年才发证明?),故不展开叙述。
于是就有基于暴力递推求逆的 $O(n\sqrt{n})$ 算法了。
练习题 : [HDU4658 Integer Partition](http://acm.hdu.edu.cn/showproblem.php?pid=4658)
本题中,每个数的使用次数不能达到 $K$ 次。有 OGF :
$$P(x)=\prod_{k=1}\sum_{i=0}^{K-1}x^{ik}=\prod_{k=1}\dfrac{1-x^{kK}}{1-x^k}$$
将分子分母分别用五边形数定理展开,然后暴力求逆 + 卷积即可。
- **Ferrers 图**
记 $P_{n,m}$ 为将 $n$ 拆分成不超过 $m$ 个无序整数的方案数。
无法沿用前文式子的思路,难以直接计算。
**定义** :在一个整数拆分中,将各个数写成“柱状统计图”的形式,即得到 Ferrers 图。
拆分 $1+1+2+4+5$ 的 Ferrers 图如下所示 :
$$
\begin{aligned}
&5 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\
&4 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\
&2 : \blacksquare\ \blacksquare\\
&1 : \blacksquare\\
&1 : \blacksquare\\
\end{aligned}
$$
要拆成不超过 $m$ 个无序整数,即 Ferrers 图的“行数”不超过 $m$。
接下来,将 Ferrers 图翻转,得到另一个 Ferrers 图,其对应另一个整数拆分 :
$$
\begin{aligned}
&5 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\
&3 : \blacksquare\ \blacksquare\ \blacksquare\\
&2 : \blacksquare\ \blacksquare\\
&2 : \blacksquare\ \blacksquare\\
&1 : \blacksquare\\
\end{aligned}
$$
$$1+1+2+4+5\ \leftrightsquigarrow\ 1+2+2+3+5$$
我们观察翻转后产生的图有什么约束,答案是 : 每一列的长度不超过 $m$。
这等价于要求用 $\leq m$ 的数来拆分,于是可以写出 OGF :
$$P_m(x)=\sum\limits_{i=0}P_{i,m}x^i=\prod_{k=1}^m\dfrac{1}{1-x^k}$$
可以使用类似的方法 $O(n\log n)$ 求解。
练习题 :[[数学记录]P5824 十二重计数法](https://www.luogu.com.cn/blog/command-block/post-shuo-xue-ji-lu-p5824-shi-er-zhong-ji-shuo-fa)
通过 Ferrers 图可以得到分拆数的另一种 $O(n\sqrt{n})$ 求解方法。
可见 : [EI : 分拆数的第三种计算方法](https://blog.csdn.net/EI_Captain/article/details/104729572)
- **杂项**
- 分拆数与时间复杂度
分拆数的估计是 $O\Big(e^{\sqrt{\small\frac{20}{3}n}}\Big)$ (据说这是拉马努金弄到的),在某些题目中枚举整数分拆能得到优秀的亚指数算法。
例题 :[P4128 [SHOI2006] 有色图](https://www.luogu.com.cn/problem/P4128)
- 一个奇怪结论
对于 $n$ 的分拆, 各个分拆方案中出现至少 $k$ 次的数的个数和,等于所有方案中 $k$ 出现的总次数。
详细讨论可见 : [Matrix67 : 整数分拆中的一个出人意料的结论](http://www.matrix67.com/blog/archives/6348)
# Ox07.多项式进阶科技 & 分析技巧
## 多项式进阶科技
“科技”指一些本身容易理解的经典问题的实际解决方案,分析过程较为简单且和题目本身的推导无关。如解决多项式乘法的 FFT。
在如此庞大的一篇文章当中出现代码框严重妨碍阅读……我就把文章分块了。
在前面我们已经学习了多项式的一些基本运算,现在来看一些新的算法。
- [从拉插到快速插值求值](https://www.luogu.com.cn/blog/command-block/zong-la-cha-dao-kuai-su-cha-zhi-qiu-zhi)
- 常系数线性递推 (咕咕咕)
- [半在线卷积小记](https://www.luogu.com.cn/blog/command-block/ban-zai-xian-juan-ji-xiao-ji)
- 多项式复合 (咕咕咕)
- Bluestein 算法 : 可见 [单位根反演小记](https://www.luogu.com.cn/blog/command-block/dan-wei-gen-fan-yan-xiao-ji)
## 多项式技巧
针对题目的分析技巧。
前面的红色部分是大技巧,后面的蓝色部分是杂碎。
本节中例题并不多,可以配合后文练习题食用。
- ### $\color{red}\bf(1)$ **多项式拉格朗日反演及其扩展**
用于快速求出多项式复合逆的某一项系数。
- **回忆** : 多项式复合: $F(G(x))=\sum\limits_{i=0}F[i]G(x)^i
说白了就是把另一个多项式代入进去。得到的还是一个多项式。常数项为 0 ,一次项系数非 0 的多项式在复合运算下形成群 。
封闭性显然。多项式复合逆有得到唯一解的构造性算法(逐位递推),故有可逆性。
多项式符合群的单位元为 x 。 于是当 F(G(x))=G(F(x))=x 时,称 F,G 互为复合逆。
注意复合运算一般并不具有结合律。
大家有兴趣的话可以去看看 P5373 【模板】多项式复合函数 和 P5809 【模板】多项式复合逆。不过朴素的(不借助题目本身性质)的复合算法在实战中并不常用。
有两个幂级数 F(x),G(x) ,有 G(F(x))=x ,即 F,G 互为 复合逆。
假如已知 F ,可以求得 G 的某一项 。
\large[x^n]G(x)=\frac{1}{n}[x^{-1}]F(x)^{-n}
------------
- **关于证明的瞎吹**
$[x^{-1}]$ 这个记号让我们感到不安,之前的所有运算都定义在自然数指数加法卷积上,这里出现了负指数。
注意到 $F,G$ 的常数项都为 $0$ ,在我们习惯的 $\pmod{x^n}$ 整式域里面甚至没有逆。
于是,引入**分式域**,即引入负整数次项。此时加法卷积仍然是良定义的。
一开始可能有点不习惯,只当是几千年前人们接受数轴负半轴的心态吧……
而且, $F,G$ 在分式域中存在逆,只不过要涉及到 $[x^{-1}]$ 项。
- **分式域上的逆**
对于无法求逆的整式,在分式域中只需适当平移即可转化为常系数非 $0$ 的整式求逆。
若 $F(x)$ 无法求逆,找出整式 $G(x)=F(x)/x^k$, 使得 $G(x)$ 有常数项,那么 $\dfrac{1}{F(x)} = x^{-k}\dfrac{1}{G(x)}
例 : (-2x^2+x)^{-1}=(-2x+1)^{-1}x^{-1}=\dfrac{x^{-1}}{1-2x} 。
在分式域中,我们仍然可以考虑加法卷积,但是工业实现中提取系数时要注意偏移量 。
引理 : 对于常系数为 0 且 [x^1] 系数非 0 的整式 F(x) ,有
[x^{-1}]F'(x)F(x)^k=[k=-1]
证明 : 当 k\neq -1 ,有 F'(x)F(x)^k=(\frac{1}{k+1}F(x)^{k+1})' 而求导不可能产生 [x^{-1}] 项。
当 k=-1 ,[x^{-1}]F'(x)/F(x)=[x^0]\dfrac{F'(x)}{F(x)/x}
现在 F(x)/x 是可逆整式,于是只需分别考虑分数线上下的常数项,发现都是 F[1] ,于是上式值为 1 。
接下来是拉格朗日反演的证明。
\begin{aligned}
G(F(x))&=x\\
\sum\limits_{i=0}G[i]F^i&=x\\
\sum\limits_{i=0}G[i]iF^{i-1}F'&=1\\
\sum\limits_{i=0}G[i]iF^{i-n-1}F'&=F^{-n}\\
[x^{-1}]\sum\limits_{i=0}G[i]iF^{i-n-1}F'&=[x^{-1}]F^{-n}\\
\sum\limits_{i=0}iG[i]\big[i-n-1=-1\big]&=[x^{-1}]F^{-n}\\
nG[n]&=[x^{-1}]F^{-n}\\
[x^n]G(x)&=\frac{1}{n}[x^{n-1}]\left(\dfrac{F(x)}{x}\right)^{-n}\\
\end{aligned}
一个更方便的形式 :
[x^{-1}]F(x)^{-n}=[x^{n-1}]\left(\dfrac{F(x)}{x}\right)^{-n}
这样 \dfrac{F(x)}{x} 可求逆,直接做多项式快速幂就好了。运算中都是整式,不需要涉及到分式域。
扩展 ① : 再复合,一般称为“扩展拉格朗日反演”
条件仍然是 G(F(x))=x , H 是另一个无要求的幂级数,有
\large[x^n]H(G(x))=\frac{1}{n}[x^{-1}]H'(x)F(x)^{-n}
证明 :
\begin{aligned}
G(F)&=x\\
H(G(F))&=H\\
T(F)&=H\\
\sum\limits_{i=0}T[i]F^i&=H\\
\sum\limits_{i=0}T[i]iF^{i-1}F'&=H'\\
\sum\limits_{i=0}T[i]iF^{i-1-n}F'&=H'F^{-n}\\
\sum\limits_{i=0}T[i]i\big[i-1-n=-1\big]&=[x^{-1}]H'F^{-n}\\
T[n]&=\dfrac{1}{n}[x^{-1}]H'F^{-n}
\end{aligned}
其中第三步记 T(x)=H(G(x)) 。
下面直接证明扩展另类拉格朗日反演,令 H(x)=x 即可得到原版本。
记 T(x)=H(G(x)) ,根据引理直接进行构造
\begin{aligned}
[x^n]H(G(x))&=\sum_{i=-\infty}^{+\infty}T[i]\big[i-n-1=-1\big]\\
&=\sum_{i=-\infty}^{+\infty}T[i][x^{-1}]F'F^{i-n-1}\\
&=[x^{-1}]F'F^{-n-1}\sum_i T[i]F^i\\
&=[x^{-1}]F'F^{-n-1}T(F(x))\\
&=[x^{-1}]F'F^{-n-1}H(G(F(x)))\\
&=[x^{-1}]F'F^{-n-1}H(x)\\
&=[x^n]H(x)\left(\dfrac{F(x)}{x}\right)^{-n-1}F'(x)
\end{aligned}
在 n=0 时有奇效。
考虑加入一元使信息分离 :
{\rm Ans[k]}=[x^ny^k]\sum\limits_{i=0}(yF(x))^k=[x^ny^k]\dfrac{1}{1-yF(x)}
注意到,如果直接取 [x^n] 项系数的多项式,我们就能得到以 y 为元的答案。
可以表示成多项式复合的形式 : H(x)=\dfrac{1}{1-xy} ,则上式为 H(F(x)) 。
设 G(x) 为F(x) 的复合逆,使用扩展拉格朗日反演可得:
[x^n]H(F(x))=\frac{1}{n}[x^{n-1}]\dfrac{y}{(1-xy)^2}\left(\dfrac{G(x)}{x}\right)^{-n}
注意到 \dfrac{y}{(1-xy)^2}=y\sum\limits_{i=0}i(xy)^i , 设 P(x)=\left(\dfrac{G(x)}{x}\right)^{-n}
则有 [x^{n-1}]y\sum\limits_{i=0}i(xy)^i\left(\dfrac{G(x)}{x}\right)^{-n}=y[x^{n-1}]P(x)\sum\limits_{i=0}i(xy)^i
考虑提取系数。
{\rm Ans[k]}=[x^{n-1}y^{k-1}]\sum\limits_{i=0}(i+1)(xy)^iP(x)
{\rm Ans[k]}=k\times P[n-k]/n
所以,只要能求出 G(x) ,就能在 O(n\log n) 内求出答案。
主要的困难在于求复合逆,一般情况下目前只能做到 O((n\log n)^{1.5}) 。
某些特殊的幂级数可能会有较为简洁的复合逆存在。
相关习题
\color{red}\bf(2) 下降幂多项式
定义 : 形如 F(x)=\sum\limits_{i=0}F[i]x^{\underline i} 的多项式。
前文讲到过,牛顿级数 和 0....n 点值之间,可以通过二项式反演 在一次卷积内变换。
回忆 : F(x)=\sum\limits_{i=0}\dbinom{x}{i}F[i]\ \ \Longrightarrow\ \ F[x]=\sum\limits_{i=0}\dbinom{x}{i}(-1)^{m-i}F(i)
注意到 F(x)=\sum\limits_{i=0}\dbinom{x}{i}F[i]=\sum\limits_{i=0}F[i]\dfrac{x^{\underline i}}{i!} ,其实和下降幂多项式等价。
点值 \large\xleftrightarrow{\text{卷积加速二项式反演}} 牛顿级数 \large\xleftrightarrow{\text{乘除}i!} 下降幂多项式
当然,还有便捷的办法。
F(n)=\sum\limits_{i=0}F[i]n^{\underline i}=\sum\limits_{i=0}^n\dfrac{n!}{(n-i)!}F[i]
\dfrac{F(n)}{n!}=\sum\limits_{i=0}^n\dfrac{1}{(n-i)!}F[i]
这意味着,点值的 EGF 是由 F(x)e^{x} 产生的。
而逆运算就是把点值的 EGF 乘上 e^{-x} 。
我们可以仿照 FFT 的思路,先转化成点值,点乘起来之后再插值回去。
不同的是,选择的点值是 0...n ,求值和插值都是由卷积完成。
P5393 下降幂多项式转普通多项式
P5383 普通多项式转下降幂多项式
都没啥好说的,一个求值一个插值,很难写就对了。所以掌握下降幂多项式之间的乘法还是很重要的。
下降幂多项式还有一个好处就是可以快速求离散积分。
处理 G[j]=\sum\limits_{i=j}^nF[i]H[i-j] 一类的卷积。(上界是 n )
可以把 F 翻转得到 F^T ,使得 F[i]=F^T[n-i] 。
式子就变为了 G[j]=\sum\limits_{i=j}^nF[n-i]H[i-j]
这样 n-i+i-j=n-j ,只和 n,j 有关,变成了加法卷积。
F(x+c)=\sum\limits_{i=0}^nF[i](x+c)^i
$=\sum\limits_{i=0}^nF[i]\sum\limits_{j=0}^i\dfrac{i!}{j!(i-j)!}x^jc^{i-j}
=\sum\limits_{i=0}^nF[i]i!\sum\limits_{j=0}^i\dfrac{x^j}{j!}\dfrac{c^{i-j}}{(i-j)!}
设 $G(x)=F(x+c)$ ,提取系数可得 :
$G[j]=\dfrac{1}{j!}\sum\limits_{i=j}^nF[i]i!\dfrac{c^{i-j}}{(i-j)!}
我们设 P[n]=F[n]n!,\ H[n]=\dfrac{c^{n}}{n!} ,则 G[j]j!=\sum\limits_{i=j}^nP[i]H[i-j]
这就是差卷积了。
应用 :
事实上,由于下降幂二项式定理的成立,下降幂多项式的平移也有类似的形式。
应用 : P5667 拉格朗日插值2
在 EGF 中,我们给 [x^n] 项附上 \frac{1}{n!} 的因子来得出二项卷积。
由于 x 的幂使得信息可以区分,最后我们能够把信息还原回来。
对于可以区分的信息 (可能靠 x 的不同次数,也可能靠下标等等) ,我们可以根据 (下标,次数) 乘上设计的因子,辅助式子的变形。
如 : [数学记录]Loj#6703. 小 Q 的序列 用 e^{-x} 导数的性质合并两项。
在自描述(写出ODE)的时候,合适的附加因子能够提供极大的帮助。
例 : P6800 【模板】Chirp Z-Transform
引理: ab=\binom{a+b}{2}-\binom{a}{2}-\binom{b}{2} ,这是一个拆卷积的常用方法。
\begin{aligned}
F(c^t)&=\sum\limits_{i=0}^nF[i]c^{it}\\
&=\sum\limits_{i=0}F[i]c^{\binom{i+t}{2}-\binom{i}{2}-\binom{t}{2}}\\
&=c^{-\binom{t}{2}}\sum\limits_{i=0}c^{-\binom{i}{2}}F[i]c^{\binom{i+t}{2}}\\
\end{aligned}
记 G[k]=c^{\binom{k}{2}},\ F_*[k]=F[k]c^{-\binom{k}{2}} ,则 F(c^t)=c^{-\binom{t}{2}}\sum\limits_{i=0}F_*[i]G[i+t] ,可以差卷积计算.
注:各个 c^{\binom{k}{2}} 可以两次前缀积计算,以减小常数。
大佬口中常出现的 \rm ODE 是 \rm ordinary\ differential\ equation 即常微分方程的缩写。
对常微分方程提取系数可以帮助我们洞察递推式 和半在线卷积 ,也可以进一步用于复合推导。
下面是一些经典的常微分方程和解 : (实战中大多数是先观察到解,然后构造方程)
G(x)=\exp A(x)\quad\Longrightarrow\quad G'(x)=G(x)A'(x)
复合一个多项式后可以计算 “部分 $\exp$ "。
设 $T(x)=G(F(x))$ ,有 $G'(F(x))=T'(x)/F'(x)$ 使用前面的结论可得 :
$T(x)=\sum\limits_{i=0}^k\dfrac{F(x)^i}{i!}\quad\Longrightarrow\quad T(x)=T'(x)/F'(x)+\dfrac{F(x)^k}{k!}
即 T'(x)=F'(x)\bigg(\dfrac{F(x)^k}{k!}-T(x)\bigg) 。
G(x)=\sum\limits_{i=0}\dfrac{x^i}{i!(i+k)!}\quad\Longrightarrow\quad G(x)=xG''(x)+(k+1)G'(x)
证明 : 观察 G'(x)=\sum\limits_{i=0}(i+1)\dfrac{x^i}{(i+1)!(i+k+1)!}=\sum\limits_{i=0}\dfrac{x^i}{i!(i+k+1)!}
对比 G'[n]=\dfrac{x^n}{n!(n+k+1)!} 和 G[n]=\dfrac{x^n}{n!(i+k)!} 发现相差 n+k+1 倍。
可以凑上 (k+1)G'(x) ,这样还差 n 倍。
考虑 (xA')[n]=nA[n] ,拿 xG''(x) 来凑即可。
G(x)=\sum\limits_{i=0}x^ii^{\underline k}\quad\Longrightarrow\quad (x^2-x)G''(x)+(k+2)G'(x)+G(x)=0
证明 : 观察 G'(x)=\sum\limits_{i=0}(i+1)x^i(i+1)^{\underline k}=\sum\limits_{i=0}x^ii^{\underline k}\dfrac{(i+1)^2}{(i-k+1)}
根据 (i+1)^2=i^{\underline 2}+3i^{\underline 1}+1 ,可凑出 x^2G''(x)+3G'(x)+G(x)=\sum\limits_{i=0}x^i(i+1)^{\underline k}=\sum\limits_{i=0}x^ii^{\underline k}(i+1)^2
设 T(x)=G'(x) ,可凑出 xT'(x)+(1-k)T(x)=\sum\limits_{i=0}x^iT[i](i-k+1)
即 xG''(x)+(1-k)G'(x)=\sum\limits_{i=0}x^ii^{\underline k}(i+1)^2=x^2G''(x)+3G'(x)+G(x)
整理得 0=(x^2-x)G''(x)+(k+2)G'(x)+G(x) 。
G(x)=(x+1)^a(x-1)^b\quad\Longrightarrow\quad G'(x)=\dfrac{aG(x)}{x+1}+\dfrac{bG(x)}{x-1}
证明 : 观察 G'(x)=a(x+1)^{a-1}(x-1)^b+b(x+1)^a(x-1)^{b-1}
不难验证结论成立。
G(x)=\sum\limits_{i=0}^k\dbinom{n}{i}x^i\quad\Longrightarrow\quad nG(x)-(1+x)G'(x)=\dbinom{n}{k}(n-k)x^k
证明 : 观察 G'(x)=\sum\limits_{i=0}^k\dbinom{n}{i}ix^{i-1}=\sum\limits_{i=0}^{k-1}\dbinom{n}{i+1}(i+1)x^i
nG(x)-(1+x)G'(x)=\sum\limits_{i=0}^k\dbinom{n}{i}(n-i)x^i-\sum\limits_{i=0}^{k-1}\dbinom{n}{i+1}(i+1)x^i=\dbinom{n}{k}(n-k)x^k
应用和推广 : [数学记录]P5401 [CTS2019]珍珠 (近线性做法)
更多相关内容可见 : \rm EI : 关于整式递推机械化的尝试
Ox08. 组合对象符号化
解析组合试图从一个较为机械化的方式帮助我们将组合计数问题从模型直接转为生成函数。——\bf E.I.
符号化组合对象,解救选手于组合意义的地狱之中。——x义x
这本书可能是我读过的最精美的书了,其中的所有证明都是那么地优雅,逻辑清晰,笔意酣畅,这大概是作者采用了优雅、有效的符号的缘故。——《具体数学 》亚马逊评论
在开始阅读之前,请先回忆 0x04 中“组合对象”,“笛卡尔积”等基本概念,它们会在下文中频繁出现。
在这一节,我们主要研究如何用生成函数来刻画组合对象,所以你可以暂时不去思考如何处理得到的生成函数。
组合结构导出生成函数
对于组合类 \mathcal A 和组合对象 a\in {\mathcal A} ,将 a 用代数对象 z 的幂表示为 z^{|a|} ,称为幂表示 。
在幂表示中,我们略去了组合对象的其他信息,只保留了“大小”这一个信息。
这里 z 只是一个服从乘法运算律的符号。
定义该组合类的生成函数 (OGF)为 :
A(z)=\sum\limits_{a\in{\mathcal A}}z^{|a|}=\sum\limits_{i=0}A[i]z^i
生成函数是幂表示的和,故也是形式幂级数。
由定义不难验证,幂表示的和代表单元素(集合)的并,生成函数的和表示集合的并。
对于组合对象 a,b 的组合 (a,b) ,有 z^{|(a,b)|}=z^{|a|+|b|}=z^{|a|}\times z^{|b|} 。于是,组合对象的组合对应幂表示的乘积。
利用乘法运算律 (a_1+a_2+...)\times (b_1+b_2+...)=a_1b_1+a_1b_2+a_2b_1+a_2b_2+... 可以验证,生成函数的乘积表示组合类的笛卡尔积。
\begin{aligned}
\mathcal{C=A+B}&\Rightarrow C(z)=A(z)+B(z)\\
\mathcal{C=A\times B}&\Rightarrow C(z)=A(z)B(z)
\end{aligned}
综上,生成函数的基本运算和组合类的“集合并”,“笛卡尔积”是同构的。我们可以将组合类的构造翻译为生成函数的运算。
记 \mathcal E=\{\epsilon \} 是只由一个大小为 0 的元素(空 )构成的组合类。有 E(z)=1 。
对于任意组合类 \mathcal A ,规定 {\mathcal A}^0=\mathcal E 。但注意 \mathcal E 并不能直接视作笛卡尔积的单位元。
记 \mathcal Z 是只由一个大小为 1 的元素构成的组合类。有 Z(z)=z 。
和 0x04 中的例子一致。
设 $01$ 串的组合类为 $\mathcal S$ ,将其内容用无穷求和的方式写出 :
$${\mathcal S}={\mathcal E}+\texttt{0}+\texttt{1}+\texttt{00}+\texttt{01}+\texttt{10}+\texttt{11}+...$$
对于某个 $01$ 串,要么为空,要么是由 $0$ 或 $1$ 接上另一个 $01$ 串而得。
写成组合符号,即 ${\mathcal S}={\mathcal E}+(\texttt{0}+\texttt{1})\times {\mathcal S}$。
翻译为生成函数则有 $S(z)=1+(z+z)S(z)$ ,可解得 $S(z)=\dfrac{1}{1-2z}$。
现在就很容易得到 $S[n]=[z^n]\dfrac{1}{1-2z}=2^n$。
卡塔兰数
卡塔兰数有一个广为人知的组合意义 : C[n]=n 个点的二叉树个数。
一个二叉树要么为空,要么由 { 根,左儿子,右儿子 } 三部分组成。则有 :
\mathcal{C=E+C\times Z\times C}
对应到生成函数,则有
C(z)=1+C(z)\cdot z\cdot C(z)
加法的扩展定义
有时候两个需要“并列“的组合类中有重复的对象,此时“不交并”的定义就不再使用。
我们定义 :
\mathcal{A+B=(A\times E_1)∪(B\times E_2)}
其中 E_1,E_2 为两个不同的只含一个大小为 0 的对象的组合类。
这个定义可以起到类似多重集的效果。
(无标号)经典的组合构造
复杂的组合类都是由其他组合类构造得来的,一个构造是从一组组合类映射到一个组合类的函数。
下面让我们来看看,在生成函数的视角中,各色组合构造会有怎样的形式。
生成函数的定义已经“翻译”了 “集合并”,“笛卡尔积” 这两个最基本的构造。
对于组合类 \mathcal A ,定义 “生成不定长序列” 构造为 :
{\rm SEQ}(\mathcal A)=\mathcal{E+A+A\!\times\!A+A\!\times\!A\!\times\!A+...}=\sum\limits_{k=0}{\mathcal A}^k
又作 {\rm SEQ}(\mathcal A)=\{(a_1,a_2,...,a_m):m\geq 0,a\in{\mathcal A}\} ,即用若干个 \mathcal A 中元素拼成的有序序列。
这里要求 A[0]=0 ,否则会在计数序列中产生无穷大。
写成生成函数,则有 :
\mathcal B={\rm SEQ}(\mathcal A)\ \Rightarrow\ B(z)=\sum\limits_{k=0}A(z)^k=\dfrac{1}{1-A(z)}
例 : 01 序列。
记 {\mathcal C}=\{\texttt{0},\texttt{1}\} 。 01 串可以看作 0,1 生成的序列,即 \mathcal S={\rm SEQ}(\mathcal C) 。
这能直接得到 S(z)=\dfrac{1}{1-C(z)}=\dfrac{1}{1-2z} 。
组合类 \mathcal A 的 “k-膨胀构造” 定义为 :
{\rm AMP}_k(\mathcal A)=\{\overbrace{(a,a,...,a)}^{\text{共 k 个}}:a\in {\mathcal A}\}
大意是说, {\rm AMP}_k(\mathcal A) 中的元素都是 \mathcal A 中某个元素复读 k 次的结果,你也可以理解成所有元素的大小都扩大 k 倍。
于是,在幂表示中将 z 简单地替换为 z^k 即可,我们有 :
{\mathcal B}={\rm AMP}_k(\mathcal A)\ \Rightarrow\ B(z)=A(z^k)
对于组合类 \mathcal A ,其中的所有对象都是 \mathcal B 中若干元素的组合。
定义 a\in{\mathcal A} 在 \mathcal B 上的拆分 为 a=(b_1,b_2,...,b_m),b\in{\mathcal B} 。(这一般应是唯一的)
记 a 的容 为 {\rm cap}_{\mathcal B}(a)=m ,即拆分中的元素个数。
令 {\bf G}=\{G_0,G_1,G_2,...\} 为一个置换群列 ,其中 G_k 包含若干大小为 k 的置换。
元素 a_1,a_2 在 \mathcal B 上拆分后在 \bf G 作用下本质相同 (等价),当且仅当 :
定义 ${\mathcal A}/{\bf G}_{\mathcal B}$ 为一个(组合类的)组合类。
对于 $a\in{\mathcal A}/{\bf G}_{\mathcal B}$ ,$a\subseteq {\mathcal A}$ ,且 $a$ 中的元素均本质相同。
若 $a_1\neq a_2$ ,则 $a_1,a_2$ 中的元素两两不等价。
将 $a$ 称为一个**等价类**。
$|a|$ 即为 $a$ 中任一个元素的大小。(不难发现 $a$ 中元素大小相同)
**例** : $01$ 序列。
令 $\bf G$ 为全体置换组成的置换群列。记 ${\mathcal C}=\{\texttt{0},\texttt{1}\},\ {\mathcal S}$ 为 $01$ 串的组合类。
$\texttt{011101}\in {\mathcal S}$ 在 $\mathcal C$ 上拆分的结果即为 $(\texttt{0},\texttt{1},\texttt{1},\texttt{1},\texttt{0},\texttt{1})$。则 ${\rm cap}_{\mathcal C}(\texttt{011101})=6$。
则 ${\mathcal S}/{\bf G}_{\mathcal C}=
\begin{aligned}
=&{\mathcal E}\\
+&\texttt{0}+\texttt{1}\\
+&\texttt{00}+\texttt{01}+\texttt{11}\\
+&\texttt{000}+\texttt{001}+\texttt{011}+\texttt{111}
\end{aligned}
为了方便和直观,我们从等价类 a 中抽其一个(字典序最小的)元素代表 a 。如 \texttt{011} 实际上代表了 \{\texttt{011},\texttt{101},\texttt{110}\} 。
令 \bf G 为全体环 置换组成的置换群列。定义“生成(无标号)环构造”为 :
{\rm CYC}(\mathcal A)=({\rm SEQ}(\mathcal A)-\mathcal E)/{\bf G}_{\mathcal A}
现在没有直观的组合符号式可以直接利用了。
为了便于理解,可以将 \mathcal A 中的元素看作珠子,而 {\rm CYC}(\mathcal A) 中的元素就是生成的项链。两条项链若能通过旋转变得相同则本质相同。
先分析 k 个珠子组成的环,记该组合类为 {\rm CYC}_k(\mathcal A)=({\mathcal A}^k)/{\bf G}_{\mathcal A} ,生成函数为 C_k(z) 。
枚举 G_k 中旋转置换的步数,旋转 i 步会产生 \gcd(i,k) 个等价类,大小均为 k/\gcd(i,k) 。
这可以看作有 \gcd(i,k) 个大小扩大 k/\gcd(i,k) 倍的珠子,即 \big({\rm AMP}_{k/\gcd(i,k)}(\mathcal C)\big)^{\gcd(i,k)} 。
根据 \rm Burnside 引理,置换下的等价类个数等于置换下不动点的平均数。故有 :
\begin{aligned}
C_k(z)&=\dfrac{1}{k}\sum\limits_{i=0}^{k-1}A(z^{k/\gcd(i,k)})^{\gcd(i,k)}\\
&=\dfrac{1}{k}\sum\limits_{d|k}\varphi(d)A(z^{d})^{k/d}
\end{aligned}
由于 \rm Burnside 只是一个关于“数目”的定理,所以这里并没有对应的组合式。
对各个 k 求和可得所有环的生成函数 :
\begin{aligned}
C(z)=&\sum\limits_{k=1}\dfrac{1}{k}\sum\limits_{d|k}\varphi(d)A(z^{d})^{k/d}\\
=&\sum\limits_{d=1}\sum\limits_{d|k}\dfrac{\varphi(d)}{k}A(z^{d})^{k/d}\\
=&\sum\limits_{d=1}\dfrac{\varphi(d)}{d}\sum\limits_{t=1}\dfrac{A(z^{d})^{t}}{t}\\
=&\sum\limits_{d=1}\dfrac{\varphi(d)}{d}\sum\limits_{t=1}\ln\Big(\dfrac{1}{1-A(z^{d})}\Big)\\
\end{aligned}
**例** : $01$ 环。
${\rm CYC}\big({\{\texttt{0},\texttt{1}\}}\big)=$ 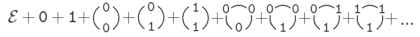
- $\bf Multiset$ **构造**
令 $\bf G$ 为全体置换组成的置换群列。定义“生成(无序)集合构造”为 :
$${\rm MSET}(\mathcal A)={\rm SEQ}(\mathcal A)/{\bf G}_{\mathcal A}$$
在无标号计数中较为常见,所以有诸如 $\rm Pólya\ Exp$ ,欧拉变换等一众别称。
在 $\bf G$ 下,$(b_1,b_2,b_3),(b_1,b_3,b_2),(b_3,b_1,b_2)$ 等都会被看做本质相同的组合。
不妨给每个元素一个字典序,将组合按照字典序排序后去重即可。
所以,等价类 个数可以转化为 字典序不降组合 的数目。
于是,按照某种顺序枚举 $\mathcal A$ 中所有对象,并一次性加入若干个,能写出 :
$${\mathcal B}={\rm MSET}(\mathcal A)=\prod\limits_{a\in{\mathcal A}}\sum\limits_{k=0}\{a\}^k$$
改写为生成函数,则有 :
$$B(z)=\prod\limits_{a\in{\mathcal A}}\sum\limits_{k=0}z^{|a|k}=\prod\limits_{a\in{\mathcal A}}\left(\dfrac{1}{1-z^{|a|}}\right)=\prod\limits_{i=1}\left(\dfrac{1}{1-z^i}\right)^{A[i]}$$
至于计算,可以尝试取 $\ln$ 再 $\exp$ :
$$
\begin{aligned}
=&\exp\ln\prod\limits_{i=1}\left(\dfrac{1}{1-x^i}\right)^{A[i]}\\
=&\exp\sum\limits_{i=1}A[i]\ln\left(\dfrac{1}{1-x^i}\right)\\
=&\exp\sum\limits_{i=1}A[i]\sum\limits_{i|j}\dfrac{ix^j}{j}
\end{aligned}
$$
暴力完成后面的求和,复杂度是 $O\big(\sum_{i=1}^nd(n)\big)=O(n\log n)$ 的。然后就是 $\exp$。
稍作代换可以得到另一个有趣的式子。
$$
\begin{aligned}
=&\exp\sum\limits_{i=1}F[i]\sum\limits_{j=1}\dfrac{x^{ij}}{j}\\
=&\exp\sum\limits_{j=1}\dfrac{1}{j}\sum\limits_{i=0}F[i]x^{ij}\\
=&\exp\sum\limits_{i=1}\dfrac{F(x^i)}{i}
\end{aligned}
$$
记 ${\rm Exp}(A(z))=B(z)$ ,称为 Polya 指数。记逆变换为 ${\rm Ln}$。
模板 : [P4389 付公主的背包](https://www.luogu.com.cn/problem/P4389)
逆变换 :[P3784 [SDOI2017]遗忘的集合](https://www.luogu.com.cn/problem/P3784)
**例** : 下文 0x09 “无标号有根树计数”。
定义“生成(无序)k-集合构造”为 :
$$\mathcal {{\rm MSET}_k(A)=A^k/{\bf G}_{A}}$$
考虑 $\rm Burnside$ 引理,记 ${\rm cir}(g)$ 为置换 $g$ 的环大小集合(多重集)。
$$
\begin{aligned}
\mathcal{B={\rm MSET}_k(A)}\ \Rightarrow\ B(z)=\dfrac{1}{k!}\sum\limits_{g\in G_k}\sum\limits_{i\in{\rm cir(g)}}A(z^{i})
\end{aligned}
$$
朴素地计算,置换高达 $k!$ 个,效率低下。
注意到本质不同的 ${\rm cir}(g)$ 是拆分数级别的,即可简化计算。
**例** : 下文 0x09 “烷基计数 加强版 加强版”。
- $\bf Power\ Set$ **构造**
定义“生成(无序)幂集构造”为 :
$${\rm PSET}(\mathcal A)=\prod_{a\in{\mathcal A}}\big(\{\epsilon\}+\{a\}\big)$$
即枚举每个元素是否存在。也可以粗略地理解为 : ${\rm PSET}(\mathcal A)=\{B\subseteq {\mathcal A}\}$。
实际上,${\rm PSET}$ 的组合意义就是 $01$ 背包。(而 $\rm MSET$ 则是完全背包)
将组合式子改写为生成函数,则有 :
$$\mathcal B={\rm PSET}(\mathcal A)\ \Rightarrow\ B(z)=\prod_{a\in{\mathcal A}}(1+z^{|a|})=\prod_{i=0}(1+z^i)^{A[i]}$$
计算时仍然取 $\ln$ 再 $\exp$ :
$$
\begin{aligned}
=&\exp\ln\prod_{i=0}(1+z^i)^{A[i]}\\
=&\exp\sum_{i=0}A[i]\ln(1+z^i)\\
=&\exp\sum_{i=0}A[i]\sum\limits_{k=1}\dfrac{(-1)^{k-1}z^{ik}}{k}\\
=&\exp\sum\limits_{k=1}\dfrac{(-1)^{k-1}}{k}\sum_{i=0}A[i]z^{ik}\\
=&\exp\sum\limits_{k=1}\dfrac{(-1)^{k-1}A(z^k)}{k}
\end{aligned}
$$
$\exp$ 之前可以 $O(n\log n)$ 暴力完成求和。
记 ${\overline{\rm Exp}(A(z))}=B(z)$ ,称为改版 Polya 指数。记逆变换为 $\overline{\rm Ln}$。
## 标号那些事
对于初学者来说,(有/无)标号计数的区分可能是一件令人头疼的事。
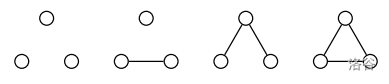
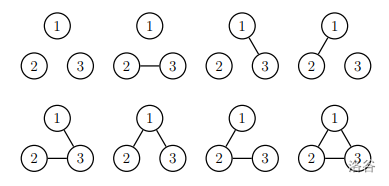
下面以简单无向图为例解释两者的区别。(例图和解说来自策爷2015年论文)
在 $n$ 个点的有标号图中,每个点被赋予了 $1\sim n$ 中的唯一标号。然而在无标号图中,各个点的地位是没有区别的。
如图,$n=3$ 时无标号简单无向图有 $4$ 种,有标号简单无向图有 $8$ 种。
- **标号的概念**
有 / 无标号组合计数几乎完全是两个体系。我们要从头开始定义“带标号组合对象”并重新使用生成函数来刻画构造方式。
对于一个带标号的组合对象对象 $a$ ,其带的标号个数恰为 $|a|$。
你可以理解为 $a$ 恰好拥有 $|a|$ 个 “节点”、“格子” 等容器(具体是什么我们并不在意),每个容器恰好可以填写一个标号。
若填写的标号恰好为 $1\sim |a|$ 的排列,则称为 **(强)标号的**。若不一定,则称**弱标号**的。记 ${\rm ind}(a)$ 为 $a$ 的标号集合。
接下来,若无特殊说明,默认所有组合对象都是带标号的。
考虑组合对象 $a,b$ 的组合积 $a\otimes b$,即从 $a,b$ 的结合能构造出什么样的组合对象。
在无标号计数中,$a\otimes b$ 的组合积被简单地定义为二元组 $(a,b)$。而有标号对象的组合积则更加复杂。
我们要求对于任意一个 $c\in|a\otimes b|$ 都有 $|c|=|a|+|b|$ 。
将标号集合 $1\sim|a\otimes b|$ **划分**为两个大小分别为 $|a|,|b|$ 的子集,然后用这两个子集的标号建立同构于 $a,b$ 的结构。
形式化地,设 $\rho(a)$ 为将组合对象 $a$ 的标号离散化后的结果,如 $\rho\big(\{1,5,7\}\big)=\{1,2,3\}$。
两个对象的组合积定义为 :
$$a\otimes b=\{(a',b'):\rho(a')=a,\rho(b')=b,(a',b')\text{是强标号的}\}$$
- **例** : 染色的纸条。
$$
{\color{blue}\blacksquare}{\color{blue}\blacksquare}\otimes{\color{red}\blacksquare}{\color{red}\blacksquare}=\{
{\color{blue}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{red}\blacksquare},
{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare},
{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare},
{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare},
{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare},
{\color{red}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{blue}\blacksquare}\}
$$
也就是将这两个纸条**归并**的所有方法。
其中 $\overset{\small 1\,\,2\,\,3\,\,4}{{\normalsize{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare}}}$ 是这样产生的 :
$a_1={\color{blue}\blacksquare}{\color{blue}\blacksquare},\ {\rm ind}(a_1)=\{1,2\}\ \longrightarrow\ a_1'={\color{blue}\blacksquare}\square\square{\color{blue}\blacksquare},\ {\rm ind}(a_1')=\{1,4\}
a_2={\color{red}\blacksquare}{\color{red}\blacksquare},\ {\rm ind}(a_2)=\{1,2\}\ \longrightarrow\ a_2'=\square{\color{red}\blacksquare}{\color{red}\blacksquare}\square,\ {\rm ind}(a_2')=\{2,3\}
将 a_2',a_2' 组合起来就得到了最终结果。
也能进一步发现,多个对象的组合积存在结合律,这说明我们的定义是好的。
两个这样的多元组判定相等,只需对每个组内元素分别判定即可(这样的定义是非常自然的)。
这个定义是递归的,何处是尽头呢?
我们在这一节中,研究的是如何刻画组合类的构造 。但构造只能结合,不能无中生有,总有一些“基本”的元素作为不可划分的万物之始。
比如有标号无向连通图计数中,“有标号无向连通图”就是不能拆分的基本元素,而一般图可以拆成若干个连通图的组合。
又比如染色问题中,单个色块就是不可拆的,但是单个色块之间的等价关系已经是明确的。
进一步地,两个组合类的笛卡尔积定义为 :
{\mathcal A}\times{\mathcal B}=\bigcup\limits_{a\in\mathcal A,b\in\mathcal B}a\otimes b
不难发现每一项 a\otimes b 各自不交。
现在要为组合积和笛卡尔积设计对应的生成函数运算。
用幂表示 改写组合对象后,需满足 : 组合积对应幂表示的乘积。
观察组合积,由集合划分的组合意义不难发现 |a\otimes b|=\dbinom{|a|+|b|}{|a|,|b|} 。
我们将 a 表示为 \dfrac{z^{|a|}}{|a|!} ,这样 a\otimes b 对应 \dfrac{\dbinom{|a|+|b|}{|a|,|b|}z^{|a|+|b|}}{|a+b|!}=\dfrac{z^{|a|+|b|}}{|a|!|b|!}=\dfrac{z^{|a|}}{|a|!}\times \dfrac{z^{|b|}}{|b|!} ,符合要求。(尝试构造时切记,幂表示只能和大小有关)
于是,定义组合类 \mathcal A 的 EGF 为 :
A(z)=\sum\limits_{a\in{\mathcal A}}\dfrac{z^{|a|}}{|a|!}=\sum\limits_{i=0}\dfrac{A[i]z^i}{i!}
同样不难验证,EGF 的乘积对应组合类的笛卡尔积。
(有标号)经典的组合构造
定义“生成序列构造”为 :
\mathcal{{\rm SEQ}(A)=E+A+A\!\times\!A+A\!\times\!A\!\times\!A+...}=\sum\limits_{k=0}{\mathcal A}^k
要求 A[0]=0 ,否则会在计数序列中产生无穷大。
解释略有不同,{\rm SEQ}(\mathcal A)=\{a_1\otimes a_2\otimes...:a\in{\mathcal A}\} 。
对于 b=(a_1,a_2,a_3) ,若其是强标号的,且 \rho(a_1),\rho(a_2),\rho(a_3)\in{\mathcal A} ,那么 b 就应该是 {\rm SEQ}(\mathcal A) 中元素。
类似无标号的情况,仍然有 :
\mathcal B={\rm SEQ}(\mathcal A)\ \Rightarrow\ B(z)=\dfrac{1}{1-A(z)}
{\rm PNT}(\mathcal A)=\sum\limits_{k=0}{\mathcal B}_k\times\{\epsilon_1,\epsilon_2,...\epsilon_k\}
组合意义是在图 a 中选择一个点作为特殊节点(根)。
不难发现,若 \mathcal B={\rm PNT}(\mathcal A) ,则 B[n]=n\cdot A[n] 。故能写出 :
B(z)=zA'(z)
记 \bf G 为全体置换组成的置换群组,将“生成集合构造”定义为 :
\mathcal{{\rm SET}(A)={\rm SEQ}(A)/{{\bf G}_{A}}}
这里的 /{{\bf G}_{\mathcal A}} 仍然有和上文中类似的定义。
先来考虑容为 k 的生成集合,设为 \mathcal{{\rm SET}_k(A)=A^k/{\bf G}} ,生成函数设为 A_k(z) 。
在有标号序列中,任意两个元素都是不同的(因为标号集合不交)。所以一种方案通过任意非单位置换后都和原来不同,故等价类的大小达到上界 k! (即 |G_k| )。
可得 :A_k(z)=\dfrac{A(z)^k}{k!}
对所有 k 求和就能得到 :
\mathcal{B={\rm SET}(A)}\ \Rightarrow\ A_k(z)=\sum\limits_{k=0}\dfrac{A(z)^k}{k!}=\exp A(z)
这一结论是我们非常熟悉的。
例 : 下文 0x09 “有标号有根树计数”
记 \bf G 为全体环 置换组成的置换群组,将“生成环构造”定义为 :
\mathcal{{\rm CYC}(A)={\rm SEQ}(A)/{{\bf G}_{A}}}
先考虑容为 k 的环,设为 \mathcal{{\rm CYC}_k(A)=A^k/{\bf G}} ,生成函数设为 A_k(z) 。类似地,由于标号序列中各个元素互不相同,等价类大小为 k=|G_k| 。
可得 :A_k(z)=\dfrac{A(z)^k}{k}
对所有 k 求和就能得到 :
\mathcal{B={\rm CYC}(A)}\ \Rightarrow\ B(z)=\sum\limits_{k=1}\dfrac{A(z)^k}{k}=\ln\Big(\dfrac{1}{1-A(z)}\Big)
顺带一提,若 \bf G 为全体环 和翻转 置换构成的群,则有 |G_k|=2k (唯一的例外是 G_1=1 ),所以在该意义下 :
\mathcal{B={\rm CYC}_{\rm flip}(A)}\ \Rightarrow\ B(z)=A(z)+\sum\limits_{k=2}\dfrac{A(z)^k}{2k}=\dfrac{1}{2}\bigg(\ln\Big(\dfrac{1}{1-A(z)}\Big)+A(z)\bigg)
例 : 基环树。(定义为 n 个点 n 条边的有标号简单无向联通图)
基环树拥有一个长度 \geq 3 的环,且每个点上面都挂着一颗树。注意这个环是没有方向的,所以还可以翻转,需要额外除以 2 。
设基环树的组合类为 \mathcal{T_{C}} ,有根树为 \mathcal T 。
于是有 \mathcal{T_{C}}={\rm CYC}_{\rm flip,\geq 3}(\mathcal T)
即 T_C(x)=\dfrac{1}{2}\sum\limits_{i=3}\dfrac{T(x)^i}{i}=\dfrac{1}{2}\Big(-\ln\big(1-T(x)\big)+T(x)+\frac{T(x)^2}{2}\Big) 。
对于组合类 \mathcal B,C ,定义“子结构构造”为 :
\mathcal{B\circ C}=\sum\limits_{k=0}{\mathcal B}_k\boxtimes {\rm SET}_k(\mathcal C)
这里的 \boxtimes 定义为 :\mathcal{A\boxtimes B=\{(a,b):a\in A,b\in B\}} ,且 |(a,b)|=|b| 。(a 只是个附上去的注解,有点像个地图,但不占实际大小)
组合意义为将 \mathcal B 的每个“节点”都换成一个 \mathcal C 中的对象。
写成生成函数的形式有 :
\mathcal{A=B\circ C}\ \Rightarrow\ A(z)=B(C(z))
在有标号计数中,诸多变换都能由 \rm Subsitution 构造导出。
大小为 $k$ 的有标号序列有 $k!$ 个。记 $S(z)=\sum\limits_{i=0}\dfrac{k!z^k}{k!}=\dfrac{1}{1-z}$ 为序列的生成函数。
则 $\mathcal {A={\rm SEQ}(B)=S\circ B}\Rightarrow A(z)=S(B(z))=\dfrac{1}{1-A(z)}
大小为 $k$ 的有标号环有 $(k-1)!$ 个。记 $C(z)=\sum\limits_{i=0}\dfrac{(k-1)!z^k}{k!}=\sum\limits_{i=0}\dfrac{z^k}{k}$ 为环的生成函数。
则 $\mathcal {A={\rm CYC}(B)=C\circ B}\Rightarrow A(z)=C(B(z))=\sum\limits_{i=0}\dfrac{A(z)^k}{k}=\ln\Big(\dfrac{1}{1-A(z)}\Big)
大小为 $k$ 的有标号无序集合(在全体置换化简下)有 $1$ 个。记 $S(z)=\sum\limits_{i=0}\dfrac{z^k}{k!}$ 为集合的生成函数。
则 $\mathcal {A={\rm SET}(B)=S\circ B}\Rightarrow A(z)=S(B(z))=\sum\limits_{i=0}\dfrac{A(z)^k}{k!}=\exp B(z)
定义 “删除构造”以及“加入构造”为 :
\begin{aligned}
{\rm DEL}(\mathcal A)&=\{b:|b|=|a|-1,a\in A\}\\
{\rm ADD}(\mathcal A)&=\{b:|b|=|a|+1,a\in A\}
\end{aligned}
组合意义就是将所有组合对象“删除”/“加入”一个点,使得这个点“参与”/“不参与”标号的分配。
若要求 A[0]=0 则有 {\rm ADD}({\rm DEL}(\mathcal A))=\mathcal A 。
比如若 {\mathcal C}={\rm ADD}\big({\rm DEL}(\mathcal A)\times \mathcal B\big) ,则可以理解为 \mathcal A 将标号 1 藏起来,不参与分配,最后再将其加回。即标号 1 一定分配给了 \mathcal A 中对象。
写成生成函数的形式,有 :
\begin{aligned}
\mathcal {B={\rm DEL}(A)}\ &\Rightarrow\ B(z)=A'(z)\\
\mathcal {B={\rm ADD}(A)}\ &\Rightarrow\ B(z)=\smallint\!\! A(z){\rm d}z
\end{aligned}
Ox09. 组合计数杂题选讲
可以当作综合练习大放送吧。
树
设为 \mathcal T ,则有 \mathcal T=Z\times{\rm SET}(T) 。则 T(z)=z*\exp T(z) 。
变形为 z=\dfrac{T(z)}{\exp T(z)} ,于是构造 A(z)=\dfrac{x}{e^x} 则有 A,T 互为复合逆。
\dfrac{F[n]}{n!}=\frac{1}{n}[x^{n-1}]{\dfrac{A(x)}{x}}^{-n}=\frac{1}{n}[x^{n-1}]e^{nx}=\dfrac{n^{n-1}}{n!}
这指出大小为 n 的有标号有根树有 n^{n-1} 种,和下文我们用 prufer 序列所得到的结果相同。
记为 \mathcal T ,则有 \mathcal{T=Z}+\sum\limits_{k\in D}{\mathcal T}^k
可以得到生成函数方程 : T(z)=z+\sum\limits_{k\in D}T(x)^k
该方程并不能像小朋友那样用求根公式解。
考虑构造 G(x)=x-\sum\limits_{k∈D}x^k 于是 G,F 互为复合逆。
接下来只需拉格朗日反演。
将非空 m 叉树记为 \mathcal T 。一颗非空 m 叉树由根和 m 棵可空 m 叉树组成。
则有 \mathcal {T=Z\times (E+T)^m} ,即 T(z)=z\big(1+T(z)\big)^m
故构造 G(x)=\dfrac{x}{(1+x)^m} ,则 T,G 互为复合逆。
套用反演公式可得 :
T[n]=\frac{1}{n}[x^{n-1}]{\dfrac{G(x)}{x}}^{-n}=\frac{1}{n}[x^{n-1}](1+x)^{mn}=\dfrac{\binom{nm}{n-1}}{n}
注意本题模数较小,计算组合数可能需要使用 \rm Lucas 定理。
考虑这样一种序列 : 长度为 n-2 ,值域在 [1,n] 以内。
奇妙的是,这类序列和带标号无根树之间存在一一对应(双射)。这对计数大有帮助。
树 \rightarrow 序列 :
每次移去所有叶子节点中标号最小的顶点和相连的边,并把与它相邻的点的编号加入 prufer 序列中。重复以上步骤直到原图仅剩 2 个顶点。
我们能够发现,节点 u 会在序列中出现 (\text{度数}-1) 次,这是个重要的性质。
序列 \rightarrow 树 :
建立集合 G 含有节点 \{1...n\} 。找出集合中最小的,未在 prufer 序列中出现过的数,将该点与 prufer 序列中首项连一条边,并将该点和序列首项删除。
重复操作 n-2 次,最后将集合中剩余的两个点之间连边。
更严谨的证明和构造算法可见 P6086 【模板】Prufer 序列。
如何构造并不是重点,我们只需要记住双射 的性质,和有关出现次数 和度数 的性质就好了。这样,就能把有标号树计数问题转化成了序列计数。
不费吹灰之力就能得到 : n 个点的有标号无根树有 n^{n-2} 种。
设(非空)无标号有根树的组合类为 \mathcal T 。一棵无标号有根树可以拆分为 根节点和各个儿子组成的森林 两部分,其中各个儿子的地位是相同的(即儿子之间可用所有置换)。
则能写出 :
\mathcal{T=Z\times {\rm MSET}(T)}
具体求解方法见 : [数学记录]P5900 无标号无根树计数
设为 \mathcal T ,则有 \mathcal {T=E+Z\times {\rm MSET}_3(T)} 。
写出 \times {\rm MSET}_3 的具体生成函数表示 :
置换 \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 1\ \ 2\ \ 3\end{matrix}\right) 的环大小集合为 \{1,1,1\} 。
置换 \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 2\ \ 1\ \ 3\end{matrix}\right) , \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 1\ \ 3\ \ 2\end{matrix}\right) , \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 3\ \ 2\ \ 1\end{matrix}\right) 的环大小集合为 \{1,2\} 。
置换 \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 3\ \ 1\ \ 2\end{matrix}\right) , \small\left(\begin{matrix}1\ \ 2\ \ 3 \\ 2\ \ 3\ \ 1\end{matrix}\right) 的环大小集合为 \{3\} 。
于是
\mathcal{B={\rm MSET}_3(A)}\ \Rightarrow\ B(z)=\dfrac{1}{3!}\sum\limits_{g\in G_3}\sum\limits_{i\in{\rm cir(g)}}A(z^{i})=\dfrac{1}{6}\big(F(z)^3+3F(z)F(z^2)+2F(z^3)\big)
这能得到方程 :
T(z)=z\dfrac{T(z)^3+3T(z)F(z^2)+2T(z^3)}{6}+1
可以化成半在线卷积,也可以牛顿迭代。
相当于求 G(F(z))=z\dfrac{F(z)^3+3F(z)F(z^2)+2F(z^3)}{6}+1-F(z) 的零点。
在求出 F(z)\bmod z^{n/2} 之后, F(z^2),F(z^3)\bmod z^n 其实都是已知的,可以(在求导中)当做常多项式来看待。
所以可求得 G'(F(z))=z\dfrac{3F(z)^2+3F(z^2)}{6}-1
牛迭的式子就是 : F(z)=F_*(z)-\dfrac{z\big(F_*(z)^3+3F_*(z)F(z^2)+2F(z^3)\big)+6-6F_*(z)}{3z\big(F_*(z)^2+F(z^2)\big)-6}
提交记录
练习题④ : Loj#6684. 有根无标号「奇树」计数
定义 \mathcal T_0 为叶子深度都为偶数的无标号有根树,\mathcal T_1 的叶子深度则为奇数。
能写出 :
$$
\begin{aligned}
\mathcal T_0&=\mathcal Z\times\big( {\rm MSET}(\mathcal T_1)-\mathcal E\big)\\
\mathcal T_1&=\mathcal Z\times {\rm MSET}(\mathcal T_0)\\
\mathcal T_1&=\mathcal Z\times {\rm MSET}\Big(\mathcal Z\times \big( {\rm MSET}(\mathcal T_1)-\mathcal E\big)\Big)\\
\end{aligned}
$$
下面将 $\mathcal T_1$ 简记为 $\mathcal T$。
写成生成函数的形式,可得 :
$$T(z)=z{\ \rm Exp}\Big({\rm Exp}\big(T(z)\big)-1\Big)$$
注意由于只算奇点,第二个 $\mathcal Z$ 不转写为 $z$。
设 $F_1(z)={\rm Exp}\big(T(z)\big),F_2={\ \rm Exp}\Big({\rm Exp}\big(T(z)\big)-1\Big)={\ \rm Exp}\big(F_1(z)-1\big)
复杂度 $O(n\log^2n)$。
[评测记录](https://loj.ac/s/1076356)
- **综合练习**
- [[数学记录]#50. 【UR #3】链式反应](https://www.luogu.com.cn/blog/command-block/post-50-ur-3-lian-shi-fan-ying)
- [[数学记录]P5206 [WC2019] 数树](https://www.luogu.com.cn/blog/command-block/post-shuo-xue-ji-lu-p5206-wc2019-shuo-shu) ( prufer序列, 子集反演, 导数缩减`DP`状态, `EGF+EXP` )
## 约束介于树与图之间的结构
没什么固定的知识点,那就一个个题目来讲好了。
- $\color{blue}\bf\Delta$ [P4233 射命丸文的笔记](https://www.luogu.com.cn/problem/P4233)
**题意** : 求所有有哈密顿回路的带标号竞赛图中,回路条数的期望。
竞赛图 : 有向图,满足每两个点之间都有一条边,但是没有规定方向。
哈密顿回路 : 不重不漏地经过每个点的环路。
首先考虑可能的哈密顿回路总数。事实上,可以视作一个环排列,所以本质不同的回路共有 $(n-1)!$ 种。
每种回路的地位都是相同的,我们数一下每条回路会在多少种竞赛图中出现。
显然,这条回路规定了恰好 $n$ 条边的方向,其余的边都随意,方案数是 $2^{\binom{n}{2}-n}
所以,回路的总条数是 :
(n-1)!2^{\binom{n}{2}-n}
现在,只需要求出“有哈密顿回路的带标号竞赛图”个数作为分母就可以了。
充要条件是 : 强连通。
如果图是非强连通的,缩点后可以当做 DAG 看待,那么一旦走到岔路里去就无法回头,肯定是无法形成回路的。
反之,根据强连通图的定义就能够构造出一个大环来。
现在问题变成了“强连通竞赛图”个数。
我们仍然考虑使用强连通竞赛图表示普通竞赛图,然后倒推。
设 F_{\rm con}(z) 是强连通竞赛图的 EGF , F(z) 则是普通竞赛图(易求,不再赘述)。
考虑将普通竞赛图缩成 DAG ,这个 DAG 仍然是竞赛图。
能够发现,由于每两个点之间都有连边, DAG 的拓扑序是唯一的。(一定要适时考虑到竞赛图的约束)
我们在此建立了双射,把 DAG 转化成了一排 强连通竞赛图。
于是 \mathcal{F={\rm SEQ}(F_{\rm con})} 。
即 F(z)=\dfrac{1}{1-F_{\rm con}(z)} ,解得 F_{\rm con}(z)=1-\dfrac{1}{F(z)} ,多项式求逆即可。
评测记录
WC2019里面曾经提到两句,今天终于有幸来做了。
我们先考虑任意的 DAG 图,能够发现,弱连通 DAG 无序组合并分配标号之后就能得到任意的 DAG 图。
那么,我们只需求出任意的 DAG 图的 EGF ,然后取 \ln 就能得到答案。
设 F[n] 为 n 个点的任意的有标号 DAG 图的方案数。
考虑 DAG 如何拆分成子问题。在对付树时,我们往往去掉根而考虑子树,而对于 DAG ,我们要考虑入度为 0 的节点。
这些点可能有很多个,需要枚举。而且我们很难统计“恰好”有 k 个入度为 0 的点的方案,所以还需熔池。
先钦定 k 个点入度为 0 ,然后这 k 个点可以向其余的 n-k 个点 (仍然是任意DAG图) 任意连边,还要分配标号,能写出:
\sum\limits_{k=1}^n\dbinom{n}{k}2^{n(n-k)}F[n-k]
这显然会重复计数,根据经典的容斥加上交错符号即可。
F[n]=\sum\limits_{k=1}^n\dbinom{n}{k}(-1)^{k+1}2^{n(n-k)}F[n-k]
考虑用卷积来描述,但是要先解决 \binom{n}{k} 以及 2^{n(n-k)} 。
对于 $2^{n(n-k)}$ ,可以使用 $n(n-k)=\binom{n}{2}-\binom{k}{2}-\binom{n-k}{2}$ 来拆分。
则有 $2^{n(n-k)}=\dfrac{2^{\binom{n}{2}}}{2^{\binom{k}{2}}2^{\binom{n-k}{2}}}$ ,非常便于卷积。
我们设 $G(x)=\sum\limits_{i=0}\dfrac{(-1)^{i+1}x^i}{i!2^\binom{i}{2}}\ $ , $\ F(x)=\sum\limits_{i=0}\dfrac{F[i]x^i}{i!2^\binom{i}{2}}
则有 F(x)=G(x)F(x)+1 (考虑清楚边界)
解得 F(x)=\dfrac{1}{1-G(x)} ,然后求 \ln F(x) 即可。(切记还原系数)
复杂度 O(n\log n) , 提交记录
设 n 个点的有标号二分图个数为 C[n] ,其 EGF 为 C(x) 。
设 n 个点的染成黑白双色,且同色不连边的图 (称作双色图) 的个数为 F[n] 。
枚举有多少个点被染成黑色,易得 F[n]=\sum\limits_{k=0}^n\dbinom{n}{k}2^{k(n-k)}
使用类似 Chirp Z-Transform 的方法可以卷积计算 F(x) :
F[n]=n!2^{\binom{n}{2}}\sum\limits_{k=0}^n\dfrac{2^{-\binom{k}{2}}}{k!}\dfrac{2^{-\binom{n-k}{2}}}{(n-k)!}
注意到一个双色图黑白互换之后仍然是双色图,那么是否有 F[n]=2C[n] 呢?
答案是否定的。反过来考虑这个映射,对于一个有标号二分图,若其分成多个连通分量,则每个连通分量都可以有各自的染色方案,并非只有 2 种对应的双色图。
(对于一个二分图,若有 k 个连通分量,则将其黑白染色的方案数为 2^k 。)
设 H[n] 为有标号连通二分图个数,F_{\rm con}[n] 为有标号连通双色图个数。
此时就有 F_{\rm con}[n]=2H[n] 。
由于双色图是连通双色图的无序集合,可得 \exp F_{\rm con}(x)=F(x) 。
即 2H(x)=F_{\rm con}(x)=\ln F(x) 。
同时又有 C(x)=\exp H(x)=\exp \frac{1}{2}F_{\rm con}(x)=\sqrt{F(x)} 。
评测记录
我们仍然考虑用子仙人掌表示自身。这需要指定一个根方便分拆子问题,有根和无根的方案数之间就相差一个n 。
设有根仙人掌的组合类为 \mathcal F 。
考虑有什么玩意和根相邻。
单独的一条边 : 边的对面也是一个仙人掌 (把被这条边连着的置为根)。
一个环 : 若有大小为 m+1 的环,就相当于额外串起了 m 个仙人掌 (把环上的点的置为根)。
注意环是可以翻转的。
我们只考虑额外的 m 个仙人掌,不难发现只能施加翻转置换而不能旋转。
定义镜像构造为 \mathcal {{\rm FLP}(A)={\rm SEQ}(A)/{\bf F}_{A}} ,其中 \bf F 由翻转置换构成。
显然,当 m\geq 2 时简单地将生成函数除以 2 即可。
则 \mathcal {B={\rm FLP}_{\geq 2}(A)}\ \Rightarrow\ B(z)=\sum\limits_{i=2}\dfrac{A(z)^i}{2}=\dfrac{A(z)^2}{2-2A(z)}
于是可以写出 :
\mathcal {F=Z\times {\rm SET}(F+{\rm FLP}_{\geq 2}(F)})
于是能得到生成函数方程 :
F(z)=z\exp\bigg(F(z)+\dfrac{F(z)^2}{2-2F(z)}\bigg)=z\exp\dfrac{2F(z)-F(z)^2}{2-2F(z)}
考虑牛顿迭代,令 G(F(z))=z*\exp\dfrac{2F(z)-F(z)^2}{2-2F(z)}-F(z) ,现在我们就是要寻找零点。
回忆牛顿迭代的公式 : F(z)=F_*(z)-\dfrac{G(F_*(z))}{G'(F_*(z))}
我们要先算个导数。计算量过大,我不想在这里展示,可见 : Link
能算得:
G'(F(z))=z\exp\left(\dfrac{2F(z)-F(z)^2}{2-2F(z)}\right)\left(1+\dfrac{F(z)(2-F(z))}{2(1-F(z))^2}\right)-1
F(z)=F_*(z)-\dfrac{2z*\exp\dfrac{2F_*(z)-F_*(z)^2}{2-2F_*(z)}-2F_*(z)}{z\exp\left(\dfrac{2F_*(x)-F_*(z)^2}{2-2F(z)}\right)\left(1+\dfrac{1}{(1-F_*(z))^2}\right)-2}
为了简化表示,我们可以令 P(z)=z*\exp\dfrac{2F_*(z)-F_*(z)^2}{2-2F_*(z)}
F(z)=F_*(z)-\dfrac{2P(z)-2F_*(z)}{P(z)\left(1+\frac{1}{(1-F_*(z))^2}\right)-2}
最后别忘记,得到的仙人掌是有根的,要除以 n 。
复杂度 O(n\log n) , 评测记录
设 \mathcal G 为好图,\mathcal G_{\rm con} 为联通好图。则显然有 \mathcal{G={\rm MSET}(G_{\rm con})} 。
能够发现,如果一个不连通的好图取补图,一定能得到一个联通好图,反之亦然,这是双射。
这只在一个地方不成立, n=1 时一个点的补图是自己。
那么,G(z)=2G_{\rm con}(z)-z+1 。 钦定 G[0]=1 。
写出生成函数形式并变形 :
\begin{aligned}
G(z)&={\rm Exp}\big(G_{\rm con}(z)\big)\\
&=\exp\sum\limits_{i=0}G_{\rm con}[i]\sum\limits_{j=0}\dfrac{z^{ij}}{j}\\
\ln G(z)&=\sum\limits_{i=0}G_{\rm con}[i]\sum\limits_{j=0}\dfrac{z^{ij}}{j}\\
\dfrac{G'(z)}{G(z)}&=\sum\limits_{i=1}iG_{\rm con}[i]\sum\limits_{j=1}z^{ij-1}\\
zG'(z)&=G(z)\sum\limits_{i=1}iG_{\rm con}[i]\sum\limits_{j=1}z^{ij}\\
\end{aligned}
则有
zG'(x)=G(z)H(z)
提取 [z^n] 系数可得
nG[n]=\sum\limits_{i=0}^nG[i]H[n-i]
注意 H[0]=0 ,实际上不需要牵涉到 G[n] ,但是会牵涉到 H[n]=\sum\limits_{i|n}iG_{\rm con}[i]=nG_{\rm con}[n]+\sum\limits_{i|n,i≠n}iG_{\rm con}[i] 。
nG_{\rm con}[n]=nG[n]-nG_{\rm con}[n]=\sum\limits_{i=1}^{n-1}G[i]H[n-i]+\sum\limits_{i|n,i≠n}iG_{\rm con}[i]
边界为 G[0]=G[1]=G_{\rm con}[1]=1 。
递推+卡常,复杂度 O(n^2) ,可以通过。
评测记录
涉及一般图
前文 : “P4841 [集训队作业2013]城市规划”
欧拉图即存在欧拉回路 (能一笔画出) 的无向图。充要条件 : 点度均为偶数,且连通。
设 n 个点的,点度均为偶数的图的个数为 F[n] 。
考虑一张 n-1 个点的任意图,通过加入一个编号为 n 的点,向点度为奇数的点连边,即可得到一张 n 个点的偶度图。
对于一张 n 个点的偶度图,通过删除编号为 n 的点后可以对应唯一的一个 n-1 个点的图。
这就证明了 n 点偶度图和 n-1 点任意图之间存在双射。
故有 F[n]=2^{\binom{n-1}{2}} 。
设 n 个点的,点度均为偶数的连通图(欧拉图)的个数为 G[n] 。
此时显然有 G=\ln F 。
考虑使用二元 GF,用 x 来标记点数,y 来标记边数。
注意标号在点上,所以 x 这一维是 EGF ,y 这一维是 OGF。
全体无向图的生成函数为 G(x,y)=\sum\limits_{i=0}\dfrac{x^i}{i!}(1+y)^{\binom{i}{2}} ,即 G[n,m]=\dbinom{\binom{n}{2}}{m} 。
与前文类似,求出 \ln G(x,y) 即可。
注意到,一般连通图缩边双联通分量之后,会变成一棵树。
对付一棵树,首选有根化。
我们设 \mathcal F 为有根连通图, \mathcal G 为有根边双连通图。
我们考虑以挂边双的方式,生成一棵树,进而展开得到连通图。
枚举根所在的边双大小 i ,这部分是 \mathcal G_i 。
再考虑其他东西怎么连到根连通块,此时每个外部连通块能且只能向根连通块连一条边,少了就会不连通,多了就会产生更大的边双。
此时根连通块一共有 i 个节点可以连边,外部的每个有根连通块连接到根边双都有 i 种方法 (根连到某个点)。
设 \mathcal R_i 为描述某个连通块连到大小为 i 的根连通块的方案的,特殊二分图的组合类。如下图 \mathcal R_5 :
白点为注记,黑点才是负责复合连通块的部位,所以这些二分图的大小都定义为 1 。于是有 R_{i}[1]=i ,其余为 0 。于是 R_i(z)=iz 。
则挂上来的一个连通块可以表示为 \mathcal {R_i\circ F} 。这部分的生成函数即为 (iz)\circ F(z)=iF(z) 。
(这是容易理解的 : 连边有 i 种方案,故直接将计数的生成函数乘以 i 。但其中的组合原理是复合)
由于连通块可以有不定多个,还需 \rm SET 构造。
枚举根联通块大小求和,我们就还原了有根连通图。则有 :
\mathcal{F=\sum\limits_{i=\textnormal 1}G_i\times {\rm SET}(R_i\circ F)}
改写为生成函数的形式,则有
\begin{aligned}
F(z)&=\sum\limits_{i=\textnormal 1}\dfrac{G[i]z^i}{i!}\exp iF(z)\\
&=\sum\limits_{i=\textnormal 1}\dfrac{G[i]}{i!}\big(z\exp F(z)\big)^i
\end{aligned}
设 H(z)=ze^{F(z)} ,能写出 F(z)=G(H(z)) ,于是 F(H^{-1}(z))=G(z) 。 (此处 H^{-1}(z) 是复合逆)
有 H(H^{-1}(z))=z (废话),套用扩展拉格朗日反演 :
可以得到 [z^n]F(H^{-1}(z))=\frac{1}{n}[z^{n-1}]F'(z)\left(\dfrac{H(z)}{z}\right)^{-n}
整理可得 [z^n]G(z)=\frac{1}{n}[z^{n-1}]F'(z)e^{-nF(z)} ,写个EXP就做完了。
最后注意 EGF 要还原,而且因为有根还得除以 n 。
评测记录
我们设 \mathcal F 为有根连通图, \mathcal G 为有根点双连通图。
这里和边双联通有有所不同,某个点可能同时被多个点双包含。
所以,我们直接考虑“根所在的点双”是有歧义的,也就会导致重复计数。
考虑在指定的根节点上重合 (大小达到 2 的)点双。对于一个点双,还能在没有用于重合的点上挂一般连通图形成有根重合块 。
枚举重合块的个数 i 。
设 \mathcal B 为有根重合块。重合块是 有根连通图 复合到 有根点双连通图 上产生的,但是有根点双的根不能参与复合。
考虑先将根去掉再加回来,设 \mathcal G_{\rm nrt,\geq 2}={\rm DEL}(\mathcal G_{\geq 2}) 为去掉根的,大小 \geq 2 的有根点双连通图。则有 G_{\rm nrt,\geq 2}(z)=G_{\geq 2}'(z) 。
则能写出 \mathcal{B={\rm ADD}(G_{\rm nrt,\geq 2}\circ F)} 。
然后将有根重合块的根重合到整个图的根上,再次将重合块的根去掉,然后做 \rm SET 再将根加回来。
于是有 B_{\rm nrt}(z)=B'(z)=G_{\rm nrt,\geq 2}\big(F(z)\big)
则能写出
\mathcal{F=Z\times{\rm SET}(B_{\rm nrt})}
改写为生成函数 :
\begin{aligned}
F(z)&=z\exp G_{\rm nrt,\geq 2}\big(F(z)\big)\\
\ln\left(\dfrac{F(z)}{z}\right)&=G_{\rm nrt,\geq 2}(F(z))
\end{aligned}
设 H(z)=\ln\left(\dfrac{F(z)}{z}\right)=G_{\rm nrt,\geq 2}(F(z)) ,已知 H(z),F(z) ,欲求 G_{\rm nrt,\geq 2}(z) 。
利用复合逆将 F 移动得到 H(F^{-1}(z))=G_{\rm nrt,\geq 2}(z) 。
注意到 F(F^{-1}(z))=z (废话),套用扩展拉格朗日反演可得:
[z^n]G_{\rm nrt,\geq 2}(z)=\frac{1}{n}[z^{n-1}]H'(z)\left(\dfrac{F(z)}{z}\right)^{-n}
得到 G_{\rm nrt,\geq 2}(z) 之后,乘以 z 就得到了 G_{\geq 2}(z) ,再加 z (一个单点)再能最终得到 G(z) 。
评测记录
设 \mathcal G 为大小在 S 内的点双的组合类。其生成函数可以大力拉格朗日反演逐个求出。
设 \mathcal F 为要求计数的图的组合类。
经过类似的分析有 F(z)=z\exp G_{\rm nrt,\geq 2}(F(z)) 。
和上一题中不同的是,这时是已知 G ,求 F 。
构造 H(z)=\dfrac{z}{\exp G_{\rm nrt,\geq 2}(z)} ,可得 H(F(z))=z ,使用普通拉格朗日反演即可。
反演中,我们要求的是 \left(\dfrac{H(z)}{z}\right)^{-n}=\Big(\exp G_{\rm nrt,\geq 2}(z)\Big)^n=\exp \Big(n\cdot G_{\rm nrt,\geq 2}(z)\Big) , 这样可以省去部分运算。
评测记录
Ox10. 附件
特殊数表 : Link
符号表
你可能从本节估计到笔者写公式的复杂度
\sum\limits_{i=0}^m\dbinom{k}{i}x^iy^{k-i} \longrightarrow\sum\limits_{i=0}^m\dbinom{k}{i}x^iy^{k-i} (求和 , 二项式系数)
\Delta,\partial \rightarrow\Delta,\partial (一些小东西)
a^{\underline{b}} \longrightarrow a^{\underline{b}} (下降幂)
a^{\overline{b}} \longrightarrow a^{\overline{b}} (上升幂)
\begin{bmatrix}a \\ b\end{bmatrix} \longrightarrow \begin{bmatrix}a \\ b\end{bmatrix} (第一类斯特林数)
\begin{Bmatrix}a \\ b\end{Bmatrix} \longrightarrow \begin{Bmatrix}a \\ b\end{Bmatrix} (第二类斯特林数)
\left\langle\begin{matrix}n \\ k\end{matrix}\right\rangle \longrightarrow \left\langle\begin{matrix}n\\k\end{matrix}\right\rangle (欧拉数)
最后的话
吾生也有涯,而知也无涯。计数领域的广阔天地,瑰丽奇景,仍待各位探寻。
历经跋涉来到这片纷繁文字的尽头,你也许有些累了吧。
\begin{bmatrix}
\text{独行的旅人啊——}\\
\text{只要眼中有星光,奇迹就不会陨落。}\\
\text{所以,请抬头仰望吧。}\\
\text{夜深了,无数颗从未见过的星星说,不会放弃我。}\\
\end{bmatrix}
祝愿读到这里,并即将离开的的同学,旅途愉快。
那么,真的再见了。
\text{To be continued...}