题解 【P6646 [CCO2020] Shopping Plans】

**题意** ： 商店里有 $n$ 个物品，每个物品有种类与价格。 对于第 $i$ 个种类，需要购买商品的个数在 $[l_i,r_i]$ 之间。 求出前 $k$ 便宜的方案的价钱，或指出不存在。 $n,m,k\leq 2\times 10^5$ ，时限$\texttt{2s}$。 ------------ - ### Part0 先介绍解决这类“前 $k$ 优”问题的一个通用思路。 我们考虑方案与方案之间的转移。 对于方案 $S$ ，记 ${\rm trans}(S)$ 为 $S$ 的后继方案集合（具体定义暂不明确）。 我们按以下流程求解问题。 - 将花费最小的方案加入小根堆中 - 重复执行直到堆为空，或已得到所有答案 - 将堆顶方案 $S$ 输出并弹出 - 将 ${\rm trans}(S)$ 中的各个方案加入堆中 考虑怎样设计 ${\rm trans}(S)$ 才能使得这个算法正确。 将 $S$ 向 ${\rm trans}(S)$ 连边，形成一张有向图。 - 所有方案形成一棵以花费最小的方案为根的外向树。 这保证了不重不漏。 - ${\rm trans}(S)$ 的权值都大于等于 $S$ 的权值。 这样，不难证明前 $k$ 优的方案构成一个包含根的联通块。我们前述的算法可以找出这个联通块。 - ### Part1 : $m=1,l=r$ 将物品按照价格从小到大排序，花费最小的方案是选择最左的 $l$ 个物品。 我们按如下的方法构造 $\rm trans$ ： - 将最左的能右移的物品右移若干，但不能跨越其他已选的物品。 不难发现，这样调整之后权值必然变大，且得到所有方案的方法数恰都为 $1$。符合我们的要求。 > 如图是一个方案对应的调整方法。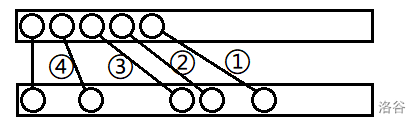 >  > 观察 ： 在任意时刻，一定是前面有一个前缀是紧密连续的，然后将这个前缀的末端向右移若干。 美中不足的是，单个 $\rm trans(S)$ 集合的大小可能达到 $O(n)$ ，不能保证复杂度。 我们改而让物品每次只能右移一位，并加入当前物品的概念，将 $\rm trans$ 改为 ： - 将当前物品改为紧密前缀的末端（最靠左的能右移的物品）。 - 将当前物品右移一位。 不难发现这两种 $\rm trans$ 是等价的。“当前物品的连续移动”对应前文“将最左的能右移的物品右移若干”。 形式化地，记 $(x,y,z)$ 表示前缀 $[1,x]$ 还没有动，当前物品位于 $y$ ，当前物品右侧的物品位于 $z$ 的方案。 转移 ： $(x,y,z)\rightarrow (x,y+1,z)$ 或 $(x-1,x+1,y-1)$。分别对应“移一步”与“ ‘当前物品’前移然后移一步”。 - ### Part1.5 : $m=1$ 只需要稍作修正，对于初始未移动的前缀 $(y-1,y,+\infty)$ ，钦定其可以转移到 $(y,y+1,+\infty)$ （多选一个）即可。 - ### Part2 : $m>1,l_i=r_i=1$ 最优方案是每个种类选择最小的。 按如下的方法构造 $\rm trans$ ： 从前往后考虑种类，记当前种类为 $p$。 - 将种类 $p$ 所选的数右移一位。 - 将 $p$ 后移若干，再将种类 $p$ 所选的数右移一位。 可惜，单个 $\rm trans(S)$ 集合的大小不能保证。 > 原先的 $\rm trans(S)$ 的结构形如图上半部。 > 我们将儿子的权值从小到大排序，然后将儿子串起来（如图下半部），即可将度数变小。 >  在本题中，我们将种类按照 最小值与次小值的差 从小到大排序，然后如此构造 $\rm trans$ ： - 将种类 $p$ 所选的数右移一位。 - 将 $p$ 后移一位，再将种类 $p$ 所选的数右移一位。 - 若 $p$ 所在种类目前选择次小值，则恢复为最小值。然后将 $p$ 后移一位，再将种类 $p$ 所选的数右移一位。 （我们的排序能保证这一步权值不降） 这一步具体的情形如下图 ：  - ### Part3 : 一般情况 考虑 **Part1.5** 中的算法，其实就是将 $m=1$ 的问题变成了一个黑箱，支持 $O(\log n)$ 得到下一个最优的解。 观察 **Part2** 中的算法，其实就是维护 $m$ 个黑箱（排好序的数组），操作中只需要访问黑箱的下一个解。 将这两个算法配合起来即可 $O(n\log n)$ 解决本题。 ```cpp #include<algorithm> #include<cstdio> #include<vector> #include<queue> #define ll long long #define pb push_back #define MaxN 200500 using namespace std; const ll INF=1ll<<60; struct Data{ int x,y,z;ll sum; bool operator < (const Data &A) const {return sum>A.sum;} }; struct SeqDS { vector<ll> ans; vector<int> a; priority_queue<Data> q; int l,r; void calc(int p) { if (p<ans.size())return ; if (q.empty()){ans.pb(INF);return ;} Data now=q.top();q.pop(); int x=now.x,y=now.y,z=now.z;ll sum=now.sum; ans.pb(sum); if (z==a.size()-1&&x+1==y&&y+1<r)q.push((Data){x+1,y+1,z,sum+a[y+1]}); if (y>=0&&y+1<=z)q.push((Data){x,y+1,z,sum-a[y]+a[y+1]}); if (x>=0&&x+1<y)q.push((Data){x-1,x+1,y-1,sum-a[x]+a[x+1]}); } void Init() { sort(a.begin(),a.end()); if (l>a.size()){ans.pb(INF);ans.pb(INF);return ;} r=min(r,(int)a.size()); ll sum0=0; for (int i=0;i<l;i++)sum0+=a[i]; q.push((Data){l-2,l-1,a.size()-1,sum0}); calc(0);calc(1); } }T[MaxN]; struct Data2{ int p,j;ll sum; bool operator < (const Data2 &A) const {return sum>A.sum;} }; int tp[MaxN]; bool cmp(int A,int B) {return T[A].ans[1]-T[A].ans[0]<T[B].ans[1]-T[B].ans[0];} priority_queue<Data2> q; int n,m,k; int main() { scanf("%d%d%d",&n,&m,&k); for (int i=1,c,x;i<=n;i++){ scanf("%d%d",&c,&x); T[c].a.pb(x); } ll sum0=0; for (int i=1;i<=m;i++){ scanf("%d%d",&T[i].l,&T[i].r); T[i].Init();tp[i]=i; sum0=min(INF,sum0+T[i].ans[0]); } sort(tp+1,tp+m+1,cmp); int cnt=0; q.push((Data2){0,0,sum0}); while(cnt<k&&!q.empty()){ Data2 now=q.top();q.pop(); int p=now.p,j=now.j;ll sum=now.sum; if (sum>=INF)break; printf("%lld\n",sum);cnt++; if (p<m&&j==1) q.push((Data2){p+1,1,sum-T[tp[p]].ans[1]+T[tp[p]].ans[0]-T[tp[p+1]].ans[0]+T[tp[p+1]].ans[1]}); if (p<m) q.push((Data2){p+1,1,sum-T[tp[p+1]].ans[0]+T[tp[p+1]].ans[1]}); if (p>=1){ T[tp[p]].calc(j+1); q.push((Data2){p,j+1,sum-T[tp[p]].ans[j]+T[tp[p]].ans[j+1]}); } }for (int i=cnt+1;i<=k;i++)puts("-1"); return 0; } ```