DS 优化建图

注：还有很多建图，本文章没有涉及到，毕竟数据结构范围很大，但是作者个人认为比较常有的建图以及其思想这里都出现了，有兴趣的读者可以自行查找的未提及的优化建图，比如根号优化，KD优化，主席树优化等题目去尝试（本质和线段树优化的思想没有太大区别 qwq）。

并且如果有typo啥的请直接洛谷私信，这篇博客的评论翻起来太麻烦了。

没有任何图片炸了。

我们从一道模板题开始优化建图之旅。

CF786B Legacy

题目大意

有 n 个点的有向图，有 3 种边，分别为

• u\to v$ 边权为 $w
• u\to $ $[l,r]$ 的所有点 边权为 $w
• [l,r]$ 的所有点 $\to u$ 边权为 $u

求从 s 号点到所有点的单源最短路。

数据范围：n,q\le 10^5

暴力

如果你不知道线段树优化建图的技巧，那么假如考场上遇到了这道题目，一个非常好做的部分分就是 O(n^2\log n) 的暴力最短路。按照题目的意思把所有边都连了（也就是 u\to [l,r] 时 u 和 [l,r] 的所有点都连上），然后跑一个 dijkstra。

对于 n,q\le 1000 还是很稳的，然而对于 n,q\le 10^5 的这个数据，你不 T 飞那么我就把这篇博客吃下去。

线段树优化建图

瓶颈在于 u\to [l,r] 的连边和 [l,r]\to u 的连边。我们既然不能一个一个连，我们说不定可以把 [l,r] 按照某种规律拆分成 \log 级别的边数。我们很自然地想到了 线段树。

先拿一个线段树过来。

对于第二个连边操作，u\to [l,r]，我们只需要从原图种的 u 连向 [l,r] 对应的线段树上的点就可以了。于是 O(n) 的边数优化成了 O(\log n)。（下图例子为 4\to [1,3]）。

（绿色边边权为 w，蓝色边边权为 0）。

但是这道题还可以区间连向点，于是我们再建立一棵线段树，方向为根向，然后相同的方法连边。（下图例子为 [1,3]\to 4。

综合起来是这样的。

最后一个问题，每棵树的叶节点其实就是绿色节点。你可以选择合并叶节点和绿色节点，也可以选择直接连 0 权无向边。我选择后者因为更加方便一点。

这个建树用 zkw 更加方便一点，但是我不会，所以就递归弄。

代码中的一些规定：第一棵线段树编号为 p，第二棵线段树编号为 p+4n，然后绿色节点 x 在图中的编号为 x+8n，这样每一个点的编号都不会相同了。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=9e5+9, M=5e6+9; //2棵线段树+普通节点 

struct edge {int to,nxt,w;}e[M]; int hd[N],tot;
void add(int u,int v,int w) {e[++tot]=(edge){v,hd[u],w};hd[u]=tot;}

int n,q,s;

struct Node {int l,r;}t[N];
void build(int p,int l,int r) {
    t[p].l=l, t[p].r=r;
    if(l==r) {
        add(l+8*n,p,0), add(p+4*n,l+8*n,0);
        add(p,l+8*n,0), add(l+8*n,p+4*n,0);
        return;
    }
    add(p,p*2,0), add(p*2+n*4,p+n*4,0);
    add(p,p*2+1,0), add(p*2+1+n*4,p+n*4,0);
    build(p*2,l,(l+r)/2), build(p*2+1,(l+r)/2+1,r);
}
void addh(int p,int x,int y,bool type,int u,int w) {
    int l=t[p].l, r=t[p].r, mid=((l+r)>>1);
    if(l==x&&y==r) {
        if(!type) return add(u+8*n,p,w);
        else return add(p+4*n,u+8*n,w);
    }
    if(y<=mid) addh(p*2,x,y,type,u,w);
    else if(x>mid) addh(p*2+1,x,y,type,u,w);
    else addh(p*2,x,mid,type,u,w), addh(p*2+1,mid+1,y,type,u,w);
}

int d[N];
namespace ShortestPath{
    bool vst[N];
    struct Node {
        int u,w;
        bool operator < (const Node &a) const {
            return w>a.w;
        }
    };
    void dijkstra() {
        memset(d,0x3f,sizeof(d)); d[s]=0;
        priority_queue<Node>q; q.push((Node){s,0ll});
        while(!q.empty()) {
            int u=q.top().u; q.pop();
            if(vst[u]) continue;
            vst[u]=1;
            for(int i=hd[u],v;i;i=e[i].nxt) {
                if(!vst[v=e[i].to]&&d[v]>d[u]+e[i].w) {
                    d[v]=min(d[v],d[u]+e[i].w);
                    q.push((Node){v,d[v]});
                }
            }
        }
    }
}

signed main() {
    scanf("%lld%lld%lld",&n,&q,&s);
    build(1,1,n);
    for(int i=1,op,v,u,w,l,r;i<=q;i++) {
        scanf("%lld",&op);
        if(op==1)
            scanf("%lld%lld%lld",&v,&u,&w), add(v+8*n,u+8*n,w);
        else if(op==2)
            scanf("%lld%lld%lld%lld",&v,&l,&r,&w),
            addh(1,l,r,0,v,w);
        else if(op==3)
            scanf("%lld%lld%lld%lld",&v,&l,&r,&w),
            addh(1,l,r,1,v,w);
    }
    s+=8*n;
    ShortestPath::dijkstra();
    for(int i=1;i<=n;i++)
        if(d[i+8*n]<2e18) printf("%lld ",d[i+8*n]);
        else printf("-1 ");
    return 0;
}

运用 zkw 线段树然后不用绿点会获得常数优化，不过这题并不需要。

[PA2011]Journeys

题目大意

$n\le 5\times 10^5, m\le 10^5

这道题和前面这题一样，甚至还更加简单一点，但是如果直接连，那么边数复杂度是 O(m\log^2 n) 的。所以我们还需要每次建两个虚点，比如说假设有一条 [2.4]\to [1,3] 的边，那么我们可以这样建。

双向边很好处理，我们把它拆成两个单向边就可以了。

绿边为 1 权边，蓝边为 0 权边，然后跑双端队列 BFS 即可。

int n,m,s,id[N],cnt;

struct Node {int l,r;}t[N];
void build(int p,int l,int r) {
    t[p].l=l, t[p].r=r;
    if(l==r) {
        id[l]=p;
        return;
    }
    add(p,p*2,0), add(p*2+n*4,p+n*4,0);
    add(p,p*2+1,0), add(p*2+1+n*4,p+n*4,0);
    build(p*2,l,(l+r)/2), build(p*2+1,(l+r)/2+1,r);
}
void adds(int p,int x,int y,bool type,int u) {
    int l=t[p].l, r=t[p].r, mid=((l+r)>>1);
    if(l==x&&y==r) {
        if(!type) return add(u,p,0);
        else return add(p+4*n,u,0);
    }
    if(y<=mid) adds(p*2,x,y,type,u);
    else if(x>mid) adds(p*2+1,x,y,type,u);
    else adds(p*2,x,mid,type,u), adds(p*2+1,mid+1,y,type,u);
}

int d[N];
void bfs() {
    deque<int>q; q.push_front(s);
    memset(d,0x3f,sizeof(d)); d[s]=0;
    while(!q.empty()) {
        int u=q.front(); q.pop_front();
        for(int i=hd[u],v;i;i=e[i].nxt)
            if(d[v=e[i].to]>d[u]+e[i].w) {
                d[v]=d[u]+e[i].w;
                if(!e[i].w) q.push_front(v);
                else q.push_back(v);
            }
    }
}

signed main() {
    scanf("%d%d%d",&n,&m,&s);
    build(1,1,n);
    cnt=8*n;
    for(int i=1,a,b,c,dd;i<=m;i++) {
        scanf("%d%d%d%d",&a,&b,&c,&dd);
        int x=++cnt, y=++cnt;
        add(y,x,1), adds(1,c,dd,0,x), adds(1,a,b,1,y);
        x=++cnt, y=++cnt;
        add(y,x,1), adds(1,a,b,0,x), adds(1,c,dd,1,y);
    }
    for(int i=1;i<=n;i++) add(id[i],id[i]+4*n,0), add(id[i]+4*n,id[i],0);
    s=id[s]+4*n;
    bfs();
    for(int i=1;i<=n;i++) printf("%d\n",d[id[i]]);
    return 0;
}

BZOJ4276 [ONTAK2015]Bajtman i Okrągły Robin

题目大意

有 n 个强盗，每个强盗会在时间段 [l,r] 中选择一个长为 1 的时间段来抢劫，且每个强盗有一个收益值 a_i。每一个长为 1 的时间段，警察只可以抓住一个强盗并获得这个强盗带来的收益。问最多可能拿到多少收益。

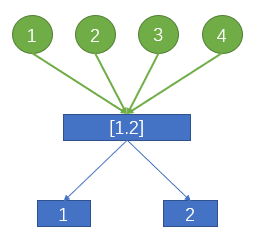
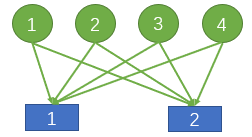
### 暴力 这是一个非常一眼的费用流（二分图最大权匹配）问题，如果不会的话左转去学费用流。所以暴力不多讲了。但是就算你费用流跑的再快，这个 $O(n^2)$ 的边数还是得让你直接爆炸。我们考虑优化建图。 ### 线段树优化建图 我们还是画一下心爱的线段树。我们看一下样例。 ``` 4 1 5 40 2 5 10 2 4 30 1 4 20 ``` 对于样例，我们很容易连边（非常 trivial，绿色强盗蓝色线段树）。  (还有一点，如果你这样建图且常数比较大的话有可能会 TLE，优化方法很简单，就像下面的代码一样，把叶节点向汇点连的边转化为根节点向汇连边，叶向树转化为根向树即可) 然后到此你就能把这道题做出来了。但是你可能有疑问，为什么这样就会有这么多优化呢？我们大致来看一个模型。  这是利用“中间商” $[1,2]$ 去建图后的图。  这是暴力建图。 我们可以看到，对于每一个完全二分图，我们把边数从乘的关系变成了加的关系，相当于把一些流先存储在 $[1,2]$ 然后再去分发给 $1$ 和 $2$。 而对于线段树上的每一个类似于“中间商”的节点，都起到了存储的作用，而为什么是 $\log$ 呢？因为线段树的高度是 $\log$，也就是说每一个流会经过 $O(\log)$ 个中间商，所以便是 $O(n\log n)$ 级别的边数。 接下来放上这题的代码。 ```cpp namespace MCMF { struct Edge {int to,nxt,c,w;}e[N*2]; int hd[N],tot; void add(int u,int v,int c,int w) {e[++tot]=(Edge){v,hd[u],c,w};hd[u]=tot;} #define debug printf("%d %d %d %d\n",u,v,c,w) void addh(int u,int v,int c,int w) {add(u,v,c,w), add(v,u,0,-w);} int s,t,cost,d[N]; bool in[N]; bool spfa() { queue<int>q; q.push(s); memset(d,0x3f,sizeof(d)); d[s]=0; while(!q.empty()) { int u=q.front(); q.pop(), in[u]=0; for(int i=hd[u],v;i;i=e[i].nxt) { if(!e[i].c) continue; if(d[v=e[i].to]>d[u]+e[i].w) { d[v]=d[u]+e[i].w; if(!in[v]) q.push(v), in[v]=1; } } } return d[t]<inf; } int dinic(int u,int flow) { if(u==t) return flow; int rest=flow; in[u]=1; for(int i=hd[u],v;i&&rest;i=e[i].nxt) if(!in[v=e[i].to]&&e[i].c&&d[v]==d[u]+e[i].w) { int use=dinic(v,min(e[i].c,rest)); if(!use) d[v]=-1; rest-=use, e[i].c-=use, e[i^1].c+=use, cost+=use*e[i].w; } in[u]=0; return flow-rest; } void clear() { memset(e,0,sizeof(e)), memset(hd,0,sizeof(hd)); tot=1; cost=0; memset(in,0,sizeof(in)); } int flow(int ss,int tt) { s=ss, t=tt; while(spfa()) while(dinic(s,inf)); return cost; } } int n,ss,tt,num; int l[N],r[N],a[N]; struct Node {int l,r;}t[N]; void build(int p,int l,int r) { t[p].l=l, t[p].r=r; if(l==r) return; int mid=(l+r)/2; build(p*2,l,mid), build(p*2+1,mid+1,r); MCMF::addh(p*2,p,mid-l+1,0), MCMF::addh(p*2+1,p,r-mid,0); } void adds(int p,int l,int r,int u) { if(t[p].l==l&&t[p].r==r) return MCMF::addh(u+20000,p,1,-a[u]); int mid=(t[p].l+t[p].r)/2; if(r<=mid) adds(p*2,l,r,u); else if(l>mid) adds(p*2+1,l,r,u); else adds(p*2,l,mid,u), adds(p*2+1,mid+1,r,u); } int main() { scanf("%d",&n); MCMF::clear(); ss=30000+1, tt=30000+2; int maxr=0; for(int i=1;i<=n;i++) scanf("%d%d%d",&l[i],&r[i],&a[i]), r[i]--, maxr=max(maxr,r[i]); build(1,1,maxr); MCMF::addh(1,tt,maxr,0); for(int i=1;i<=n;i++) MCMF::addh(ss,i+20000,1,0); for(int i=1;i<=n;i++) adds(1,l[i],r[i],i); printf("%d\n",-MCMF::flow(ss,tt)); return 0; } ``` ## 不止是线段树 有一些题目，它并不能用线段树做多少事情，但是却可以用类似的想法，建造一个数据结构，然后减少边的数量。比如这道题。 Walk （你们可以搜到这道题，但我找不到哪里可以提交的 OJ）。 ### 题意描述 > 在比特镇一共有 $n$ 个街区，编号依次为 $1$ 到 $n$，它们之间通过若干条单向道路连接。比特镇的交通系统极具特色，除了 $m$ 条单向道路之外，每个街区还有一个编码 $val_i$，不同街区可能拥有相同的编码。如果 $val_i \text{ and } val_j = val_j$，那么也会存在一条额外的从 $i$ 出发到 $j$ 的单向道路。 >Byteasar 现在位于 $1$ 号街区，他想知道通过这些道路到达每一个街区最少需要多少时间。因为比特镇的交通十分发达，你可以认为通过每条道路都只需要 1 单位时间。 >$n,m\le 300000, val\le 2^{20}$。 ### 优化建图 暴力非常显然，把边全部建出来，图是建好了，评测结果便 T 飞了。 既然题目中考虑二进制 $\text{and}$ 操作，那么我们拆位看看。我们假设最大的 $val$ 不超过 $(111)_2$，并且我们把所有的 $val$ 按照每一个二进制数中含有的 $1$ 的个数来进行整理。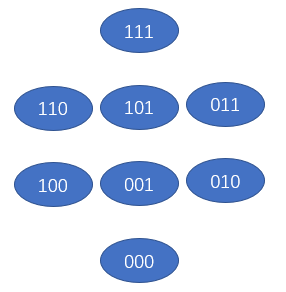  然后我们再自己创造一个样例。假设这些点的 $val$ 为 $\{7,2,5,3,0\}$。我们暴力建边是这样的。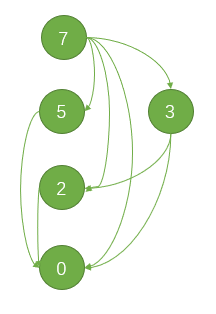  我们发现有很多冗余的边。冗余的边主要来自于 **$i\text { and } j=j$** 的所有连边其实是个传递闭包。是什么传递闭包呢？是这张图的传递闭包。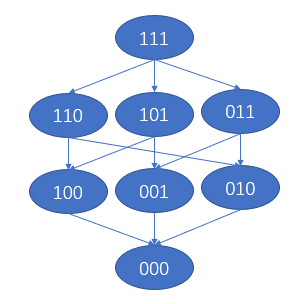  所以实际上我们并不需要 $O(n^2)$ 的连边，因为上图已经足以表示对于所有满足 $i\text { and } j=j$ 的 $(i,j)$ 存在一条 $i\to j$ 的路径。我们按照以前的思想，把原图搬到这张图上。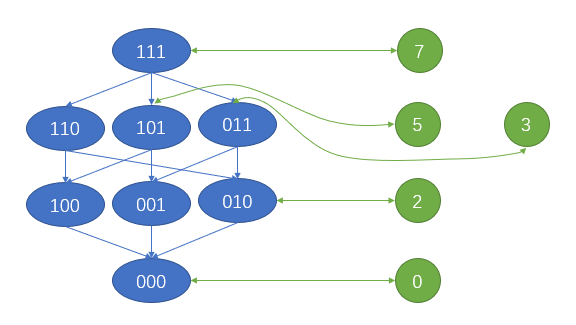  于是大功告成！对于 $m$ 条单向道路，直接在绿点上建即可。蓝边的边数为 $O(val\log (val))$，绿边边数为 $O(n+m)$，其中蓝边为无权有向边，绿边为有权边，然后建图跑双端队列 BFS 即可。 ```cpp #include<bits/stdc++.h> using namespace std; const int N=2e6+9, M=1e7+2e6+9, base=(1<<20); struct edge {int to,nxt,w;}e[M]; int hd[N],tot; void add(int u,int v,int w) {e[++tot]=(edge){v,hd[u],w};hd[u]=tot;} int n,m,d[N]; void bfs() { deque<int>q; q.push_front(1+base); memset(d,0x3f,sizeof(d)); d[1+base]=0; while(!q.empty()) { int u=q.front(); q.pop_front(); for(int i=hd[u],v;i;i=e[i].nxt) if(d[v=e[i].to]>d[u]+e[i].w) { d[v]=d[u]+e[i].w; if(!e[i].w) q.push_front(v); else q.push_back(v); } } } int main() { scanf("%d%d",&n,&m); for(int i=0;i<=base;i++) { for(int j=0;j<=21;j++) if((1<<j)&i) add(i,i^(1<<j),0); } for(int i=1,v;i<=n;i++) scanf("%d",&v), add(i+base,v,0), add(v,i+base,1); for(int i=1,u,v;i<=m;i++) scanf("%d%d",&u,&v), add(u+base,v+base,1); bfs(); for(int i=1;i<=n;i++) printf("%d ",(d[i+base]>1e9? -1 : d[i+base])); return 0; } ```