浅谈高斯消元拓展之 band-matrix
Froggy
·
·
算法·理论
前言
这是个在 OI 中很经典的 trick。(IOI2020集训队作业中就有一道需要用这个东西的题目。)
前置技能:高斯消元
注意 $\mathrm{band-matrix}$ 只是**一种特殊矩阵的名称而不是算法名称**。
处理这种矩阵依然需要**高斯消元**。
在求期望的时候经常用到。当然求解行列式的时候应该也可能会用到(比如 $\mathrm{matrix-tree}$ 定理的运用)。
(听说杜老师比较喜欢考?)
---
## 简介
顾名思义,$\mathrm{band-matrix}$ 就是长条状的矩阵(大雾)。
具体长这个样子:

空白部分都为 $0$,橙色部分可以为任何数。
这样中间就形成了一个宽度大约为 $d$ 的带。
把这种特殊的矩阵进行特殊的消元方法只需要 $\mathcal{O}(nd^2)$ 的复杂度,但是最普通的高斯消元需要 $\mathcal{O}(n^3)$ 。~~(听起来是不是很nb)~~
---
## 消元
仔细观察这用有特殊性质的矩阵,任意一个 $i$ 满足从第 $i$ 行第 $i$ 列向右拓展有不超过 $d-1$ 个非零数字,向下拓展有不超过 $d-1$ 个非零数字。
这就意味着有很多位置根本不需要消。
具体说来,假设现在要消第 $i$ 列,那么从第 $i$ 行开始往下枚举 $d-1$ 行,每行往右消 $d$ 个数字就行了。最后还是能得到一个上三角矩阵。
同时注意如果是个方程组,那么需要再把增广矩阵的最后一列消一下。
设矩阵为 $G$。
与普通高斯消元有点不一样的地方在于当 $G_{i,i}=0$ 即主元为 $0$ 的时候的处理方法。
回忆一下普通高斯消元是怎么处理的?将第 $i$ 行与它下面的主元位置非 $0$ 的某行进行交换。
杜老师曾经讲课说 $\mathrm{band-matrix}$ 就不能这么消元了。
看图:
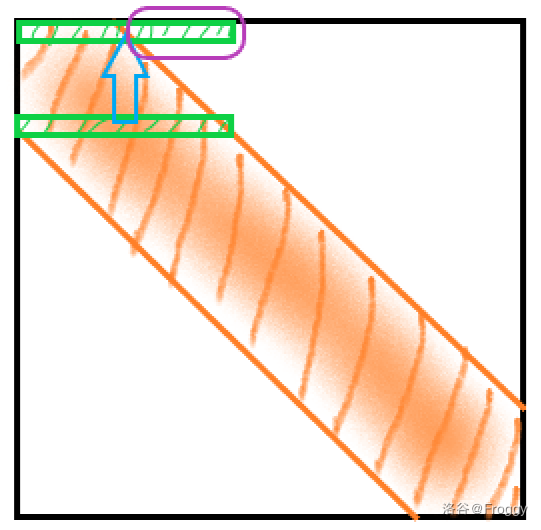
现在把下面绿色换到上面去,消元后就变成这个样子了:↓
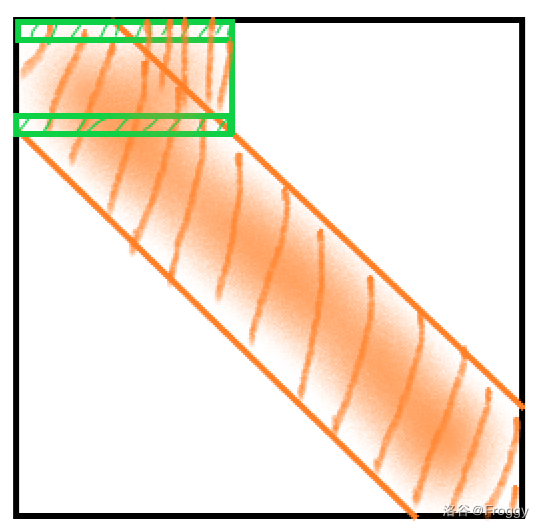
杜老师:“右边又多了一块,明显破坏了带状的性质,所以我们不能这么做。”
**真的不能做么??** 我又思考了一下,每次右边最多多出来 $d$ 个数,所以保险起见**每次往右消元 $2d$ 个数即可**,这样只是多出来一个 $2$ 倍常数。
还有一种换元方法(就是杜老师讲的那种),就是交换列。
见下图:
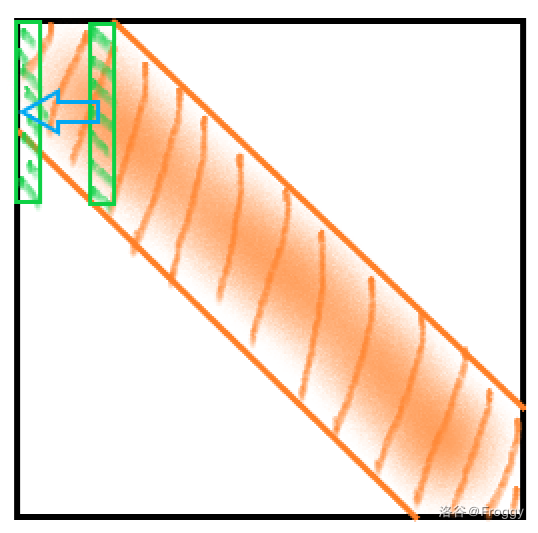
这样往下消的之后就顺便把多出来的绿色的部分消掉了。由于把列交换了所以**还需要记录 $from_i$ 表示第 $i$ 列表示的是最开始的第几个元**。
其实还是交换行比较方便,是不是?^_^。
就这么简单?!举个 $n=4,d=2$ 的例子吧。
$\begin{bmatrix}
1 & 2 & 0 & 0 & \mid & 5 \\
2 & 4 & 5 & 0 & \mid & 25 \\
0 & 3 & 4 & 1 & \mid & 22 \\
0 & 0 & 2 & 3 & \mid & 18 \\
\end{bmatrix}
首先消第 1 列,只用往下消 d-1=1 行就行了,按照普通高斯消元的方法,把第 j 行第 k 数字都减去 \dfrac{G_{j,i}}{G_{i,i}}\cdot G_{i,k}。
由于是带状矩阵,利用这个性质,每行从 i 开始消 d 个即可,第一轮消完后的矩阵变为:(别忘了把最后一列也消一下)。
1 & 2 & 0 & 0 & \mid & 5 \\
0 & 0 & 5 & 0 & \mid & 15 \\
0 & 3 & 4 & 1 & \mid & 22 \\
0 & 0 & 2 & 3 & \mid & 18 \\
\end{bmatrix}
这时候该消第 2 列了,但是发现 G_{2,2}=0,这时候就要换元。
第 3 行的主元不为 0 所以把第 2 行和第 3 行的交换一下。
提示: 如果此时第 3 行也为 0 那么方程组就会无解/存在自由元。
(大家也可以手动尝试一下如果是用交换列的方法最后得到的矩阵是什么。)
1 & 2 & 0 & 0 & \mid & 5 \\
0 & 3 & 4 & 1 & \mid & 22 \\
0 & 0 & 5 & 0 & \mid & 15 \\
0 & 0 & 2 & 3 & \mid & 18 \\
\end{bmatrix}
这时候如果有行需要消元那么就要消 2d 个数,但是目前没有需要消的行。所以直接开始消第 3 列。
$\begin{bmatrix}
1 & 2 & 0 & 0 & \mid & 5 \\
0 & 3 & 4 & 1 & \mid & 22 \\
0 & 0 & 5 & 0 & \mid & 15 \\
0 & 0 & 0 & 3 & \mid & 12 \\
\end{bmatrix}
大功告成,成功削成了一个上三角矩阵。接下来就是常规操作了,从下往上会带即可,不再赘述。
(有一点就是第 i 行从第 i 列开始往右最多有 2d 个所以只用枚举到 \min\{i+2d,n\} 即可,这一部分的复杂度就优化到了 \mathcal{O}(nd) 了。)
最后的解就是:
x_1=1 \\
x_2=2 \\
x_3=3 \\
x_4=4 \\
\end{cases}
检查一下算的对不对^_^
最后讲一下判断无解/存在自由元的方法。(其实和普通的高斯消元没什么区别)
如果某一列都无法换主元那么直接跳过,消下一个元即可。
消到最后一定存在某一行前 n 个数(也就是等式左边的系数)全部是 0。若第 n+1 个数不为 0 那么一定无解,否则存在自由元。带状矩阵只用检查 i\sim i+2d 的数即可。
就是说如果存在一个行向量最后长这个样子:
0 & 0 & \cdots & 0 & \mid & x \\
\end{bmatrix}
如果 x\neq0 则无解,否则存在自由元。
最后放一下代码吧~
void Guass(int n,int band,double *ans){
for(int i=1;i<=n;++i){
if(fabs(g[i][i])<eps){
for(int j=i+1;j<=min(n,i+band);++j){
if(fabs(g[j][i])>eps){
for(int k=i;k<=min(n,i+2*band);++k){ //换元
swap(g[i][k],g[j][k]);
}
break;
}
}
}
if(fabs(g[i][i])<eps)continue;
for(int j=i+1;j<=min(i+band,n);++j){ //往下消d行
double div=g[j][i]/g[i][i];
for(int k=i;k<=min(i+2*band,n);++k){ //往右消2d列
g[j][k]-=div*g[i][k];
}
g[j][n+1]-=div*g[i][n+1]; //把最后一列也消一下
}
}
for(int i=n;i>=1;--i){ //回带求最后答案
ans[i]=g[i][n+1];
for(int j=i+1;j<=min(i+2*band,n);++j){
ans[i]-=g[i][j]*ans[j];
}
ans[i]/=g[i][i];
}
}
最后一个问题。
Q:如果 n 太大数组存不下怎么保证复杂度?
A:像我这种懒人直接用 unordered_map 了,也可以把 g_{i,j} 映射到 g_{i,j-i} 以方便开数组。 有兴趣可以看看这道题目 CF1349D。(当然这题最正确的做法是线性高斯消元)
例题
CF24D Broken robot
经典随机游走问题。
记 dp_{i,j} 表示机器人在 (i,j) 这个格子期望还需要走多少步才能到最后一行。
$$dp_{i,j}=\begin{cases}
\frac{1}{4}(dp_{i,j}+dp_{i-1,j}+dp_{i,j-1}+dp_{i,j+1})+1,\ \ 1<j<m \\
\frac{1}{3}(dp_{i,j}+dp_{i-1,j}+dp_{i,j+1})+1,\ \ j=1 \\
\frac{1}{3}(dp_{i,j}+dp_{i-1,j}+dp_{i,j-1})+1,\ \ j=m
\end{cases}$$
(需要特判一下 $m=1$ 的情况)
直接高斯消元 $\mathcal{O}(n^3m^3)$ 直接GG。
考虑机器人只能往下走但是不能往上走,所以第 $i$ 行的期望只与第 $i-1$ 行有关,所以只用依次把每行高斯消元即可。
复杂度优化成了 $\mathcal{O}(nm^3)$ 还是GG。
把消元前的矩阵输出然后观察一下,欸这不就是 $d=2$ 的时候的带状矩阵么?!
直接套用刚才讲的方法,由于 $d^2$ 是个常数所以复杂度降为 $\mathcal{O}(nm)$ 即可通过。
[*code here*](https://www.luogu.com.cn/paste/920t0a1m)
---
#### [CF963E Circles of Waiting](https://www.luogu.com.cn/problem/CF963E)
还是经典随机游走问题。
把所有满足 $i^2+j^2\leq R^2$ 的点依次编号,显然有 $\mathcal{O}(R^2)$ 个点。
按照套路,$dp_{id(i,j)}$ 表示 $(i,j)$ 这个点走出圆还期望需要多少步。
一个点 $(i,j)$ 只用转移到 $(i,j-1),(i-1,j),(i,j+1),(i+1,j)$ 。因为是依次编号,所以可以保证这样建出来的矩阵的带宽是不超过 $R$ 的。(即 $d\leq R$ )
套用带状矩阵的消元方法,时间复杂度:$\mathcal{O}(R^2d^2)=\mathcal{O}(R^4)$。
[*code here*](https://www.luogu.com.cn/paste/tffxow5y)
---
#### [P4457 [BJOI2018]治疗之雨](https://www.luogu.com.cn/problem/P4457)
这道题目算是 $\mathrm{band-matrix}$ 的变形。
设 $dp_i$ 表示第一个数为 $i$ 时期望多少轮才能结束。
每轮第一步很好办,$+1$ 的概率是 $\frac{1}{m+1}$,不变的概率是 $\frac{m}{m+1}$。
下面 $k$ 步,考虑第一个数被减 $j$ 次的概率是多少。
那么一定是有 $j$ 次选中了然后 $k-j$ 次没选中。
概率就是 $d_j=C_{k}^j(\frac{1}{m+1})^j(\frac{m}{m+1})^{k-j}
$dp$ 方程就显然了:
$$dp_i=1+\sum\limits_{j=0}^{\min\{i,k\}}\left(\frac{m}{m+1}dp_{i-j}+\frac{1}{m+1}dp_{i-j+1}\right)d_j$$
当然 $i=n$ 的时候需要特殊处理。
观察这个式子,$dp_i$ 只与 $dp_0\sim dp_{i+1}$ 有关,所以这个矩阵就长类似于这个样子:
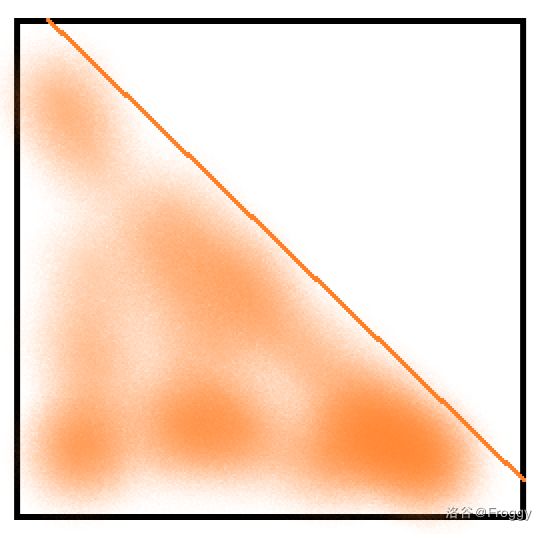
欸这不像是带状矩阵。。
但是仔细观察,右上部分都是 $0$,说明消每一行的时候只用往右消 $2$ 个就行了。
时间复杂度是 $\mathcal{O}(n^2d)$ 。其中 $d=2$ 可以看作常数。
**注意:** 这用情况下就不能使用交换行向量的做法了,否则就真的破坏带状的性质了。
[*code here*](https://www.luogu.com.cn/paste/8s8ks9k7)
---
#### [[ICPC2014 WF]Pachinko](https://www.luogu.com.cn/problem/P6899)
(2020集训队作业)
板子题。
---
## 总结:
高斯消元这个东西还是比较活的。**不要只会背板子,理解更重要,这样才能在该用的时候用到它。**
---
(有错误欢迎指出,我会感激万分)