P8865 [NOIP2022] 种花
一扶苏一
·
·
题解
P8865 [NOIP2022] 种花
Analysis
C 的方案数
首先考虑统计 \texttt{C} 形图案。
考虑枚举 \texttt{C} 形图案左下角的折角处,即如下用 * 和 & 表示的 \texttt{C} 的 & 位置:
***
*00
&**
先确定底边的的方案数:设某个位置 (i,j) 是图案的左下角,那么该点右侧所有不经过土坑的长度至少为 2 的横线都可以成为底边。设 \mathrm{right}_{i,j} 表示格子 (i,j) 向右延申的最长连续非土坑的长度,则底边的方案数即为 \mathrm{right}_{i,j} - 1(这里要求 (i,j) 不是土坑)。
$$\mathrm{right}_{i,j} = \begin{cases}0, &a_{i,j} = 1 \\ 1 , &j = m \\ \mathrm{right}_{i,j+1} + 1, & \text{otherwise}\end{cases}$$
再考虑确定其余两条边的方案数。考虑画出这两条边其实就是从枚举的左下角折点起,向上画一条长度至少为 $2$ 的边,从这条竖边的上顶点画一条横边。设当前枚举到格子 $(i,j)$,该格子正上方离它最近的土坑是 $(k,j)$,那么对于 $k < h < i+1$,$(h,j)$ 到 $(i,j)$ 可以做竖边,$(h,j)$ 右侧的边可以做 $\texttt{C}$ 的顶边。如图是两种竖边和顶边的画法。
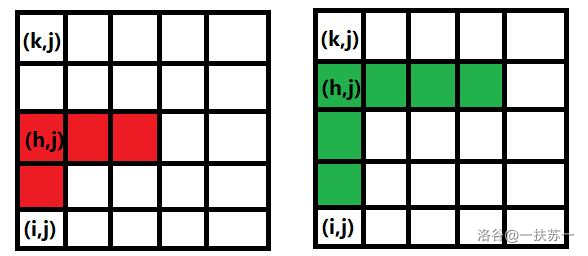
注意到格子 $(h,j)$ 对应的顶边方案数恰好也是 $\mathrm{right}_{h,j} - 1$。确定了 $(h,j)$ 的位置以后,竖边的画法是唯一的,于是竖边和顶边的方案数是 $\sum_{h = k + 1}^{i - 2} (\mathrm{right}_{h,j} - 1)$。这里要求 $(i - 1,j)$ 不是土坑。
设 $\mathrm{up}_{i,j}$ 表示以 $(i,j)$ 为左下角折点时的竖边和顶边的方案数(也就是上式),则有递推式:
$$\mathrm{up}_{i,j} = \begin{cases}0, & i = 1 \lor i = 2\\ 0, & a_{i - 2,j} = 1 \lor a_{i - 1,j} = 1 \lor a_{i,j} = 1 \\ up_{i - 1,j} + \mathrm{right}_{i - 2,j} - 1, &\text{otherwise}\end{cases}$$
把底边和另两条边的方案乘起来就是该点对应的全部方案。于是 $\texttt{C}$ 图形的总方案数为 $\sum_{i = 1}^n \sum_{j = 1}^m \mathrm{up}_{i,j} \times (\mathrm{right}_{i,j} - 1)
F 的方案数
再考虑计算 \texttt F 的方案数。注意到 \texttt{F} 形图案能且只能在 \texttt{C} 形图案的竖线下方(也就是上文字符图的 & 处)接上一条长度至少为 1 的竖线得到。对每个 \texttt C 形图案,只需要计算其下方接上的竖线的最长长度即可。
如下图是一个例子,红色表示 \texttt C 的部分,接上绿色的竖线后就构成了 \texttt F。
设 \mathrm{down}_{i,j} 表示 (i,j) 格向下延申的最长非土坑的长度,有递推式:
\mathrm{down}_{i,j} = \begin{cases}0, &a_{i,j} = 1 \\ 1, &i = n \\\mathrm{down}_{i + 1, j} + 1, &\text{otherwise}\end{cases}
于是 (i,j) 点对应的 \texttt F 的方案数就是 \mathrm{up}_{i,j} \times (\mathrm{right}_{i,j} - 1) \times (\mathrm{down}_{i,j} - 1)。总的 \texttt{F} 方案数即为 \sum_{i = 1}^n \sum_{j=1}^m \mathrm{up}_{i,j} \times (\mathrm{right}_{i,j}-1) \times (\mathrm{down}_{i,j} - 1)。
Code
代码中稍有不同的是,格点坐标的范围是 [0,n - 1] 和 [0, m - 1],其余与上文叙述一致。
在对效率没有较高要求时,熟练使用 vector 可以避免一切清空问题[狗头]
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
const int p = 998244353;
int T, id, n, m, c, f;
int main() {
for (std::cin >> T >> id; T; --T) {
std::cin >> n >> m >> c >> f;
std::vector<std::string> a(n);
std::vector<std::vector<int>> right(n), up(n), down(n);
for (auto &u : right) u.resize(m + 1);
for (auto &u : up) u.resize(m + 1);
for (auto &u : down) u.resize(m + 1);
std::generate_n(a.begin(), n, []() -> std::string { std::string s; std::cin >> s; return s; });
int ans1 = 0, ans2 = 0;
for (int i = n - 1; i; --i) {
for (int j = 0; j < m; ++j) if (a[i][j] != '1') {
if (i < n - 1) down[i][j] = down[i + 1][j] + 1;
else down[i][j] = 1;
}
}
for (int i = 0; i < n; ++i) {
for (int j = m - 1; j >= 0; --j) if (a[i][j] != '1') {
right[i][j] = right[i][j + 1] + 1;
if (i > 1 && a[i - 1][j] != '1' && right[i - 2][j] > 0) up[i][j] = up[i - 1][j] + right[i - 2][j] - 1;
int c = (right[i][j] - 1) * up[i][j] % p, f = 1ll * c * (down[i][j] - 1) % p;
if ((ans1 += c) >= p) ans1 -= p;
if ((ans2 += f) >= p) ans2 -= p;
}
}
std::cout << ans1 * c << ' ' << ans2 * f << '\n';
}
}