题解 AT2370 【[AGC013D] Piling Up】
ez_lcw
·
·
题解
考场上用了一种奇怪的做法,不知道为什么就对了,考完后仔细想才想明白。
很巧妙的一种 dp 方式。
首先发现每次操作是拿一个球、放两个球、再拿一个球,总球数不变,所以有 \text{黑球数}=n-\text{白球数}。
那么可以设 dp(i,j) 表示 i 次操作后,当前箱子里白球还剩 j 个所得到的的颜色序列的情况数。
显然有状态转移:
-
dp(0,i)=1$,$0\leq i\leq n
-
当 i>0 时,有:
\begin{aligned}
dp(i,j)=&\underbrace{dp(i-1,j)}_{\text{先白后黑,需保证$j>0$}}+\underbrace{dp(i-1,j)}_{\text{先黑后白,需保证 $n-j>0$}}+\\
&\underbrace{dp(i-1,j-1)}_{\text{先黑后黑,需保证 $j> 0$}}+\underbrace{dp(i-1,j+1)}_{\text{先白后白,需保证 $n-j>0$}}
\end{aligned}
但是发现会算重。
原因是有可能一些相同的操作(即相同的颜色序列)被开始白球数不同的多种情况计算了多次。
比如说像上图一样,用一条折线代表一种情况。尽管两种情况初始白球数量不一样,结束时白球数量不一样,但是拿出来的球颜色序列是一样的。
所以需要找到一个恰当的方法,去除这些重复的部分。
考虑钦定只计算某一种特定的方案。
发现选 0 这个点是最合适的,就是说,我们只计算所有颜色序列的情况中,白球数曾经是 0 的那一个。
放到图上来,就是只计算经过 x 轴的那条折线。
显然这种折线只有一条,因为折线不能跨越 x 轴,即白球数量在 dp 过程中不可能小于 0。
这种特殊的性质主要取决于我们不需要更新白球数量小于 0 的部分,我们也不需要用白球数量小于 0 的部分来更新其他状态。
然后考虑如何计算这种情况的方案数,最简单的就是直接设 dp(i,j,1/0) 表示前 i 次操作,当前箱子里还剩下 j 个白球,白球数量是/否达到过 0 的情况数。
当前还有好写一点的,也就是我要介绍的这种方法。
设按照我们一开始说的方法 dp,n=x 的情况下的答案是 solve(x),那么答案就是 solve(n)-solve(n-1)。
怎么理解呢?
$solve(n-1)$ 表示的是当初始球数为 $0\sim (n-1)$ 时的答案。但是在这里,我们把它理解为初始球数为 $1\sim n$,且每时每刻箱子里的白球都大于等于 $1$ 个时的答案。也就是说我固定住一个白球在箱子里不动。
那么相减是什么意思呢?
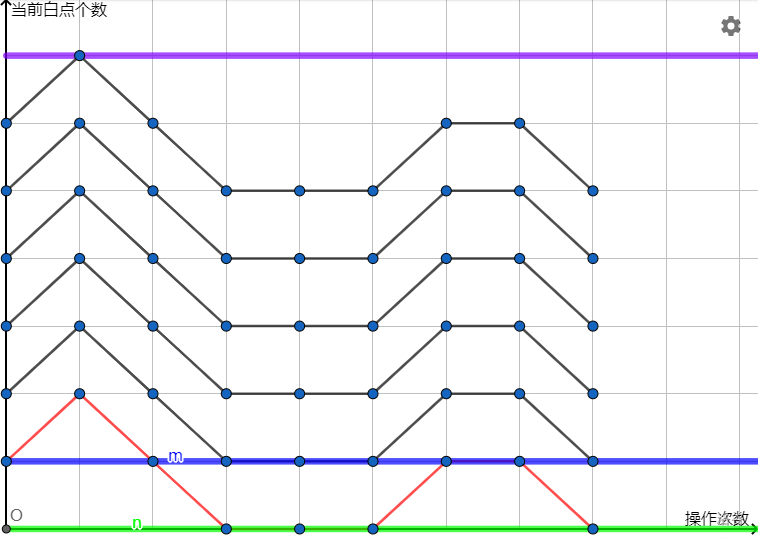
如图,$solve(n)-solve(n-1)$ 其实可以看做图中 $\color{green}{\text{绿线}}$ 与 $\color{purple}{\text{紫线}}$ 围住的情况数减去 $\color{blue}{\text{蓝线}}$ 与 $\color{purple}{\text{紫线}}$ 围住的情况数,那么最后在这些颜色序列相同的情况中,只剩下了唯一的 $\color{red}{\text{红色折线}}$ 所代表的方案。
所以这种方法也是可行的。
代码如下:
```cpp
#include<bits/stdc++.h>
#define N 3010
#define mod 1000000007
using namespace std;
int n,m,dp[N][N];
int solve(int n)
{
memset(dp,0,sizeof(dp));
for(int i=0;i<=n;i++) dp[0][i]=1;
for(int i=0;i<m;i++)
{
for(int j=0;j<=n;j++)
{
if(j) dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;//先白后黑
if(n-j) dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;//先黑后白
if(j) dp[i+1][j-1]=(dp[i+1][j-1]+dp[i][j])%mod;//白白
if(n-j) dp[i+1][j+1]=(dp[i+1][j+1]+dp[i][j])%mod;//黑黑
}
}
int ans=0;
for(int i=0;i<=n;i++)
ans=(ans+dp[m][i])%mod;
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
printf("%d\n",(solve(n)-solve(n-1)+mod)%mod);
return 0;
}
```