抛弃随机,保持理性——Leafy Tree 到 WBLT
StayAlone
·
2023-01-10 22:51:30
·
算法·理论
博客园
FHQ Treap 是当前流行的一种易于实现、易于理解、功能全面的平衡树。它可以实现文艺平衡树以及可持久化,唯一的缺点是常数略大。
这篇文章讲解了 Leafy Tree。以它实现的加权平衡树码量与 FHQ 相近,结构与线段树类似,可以像 FHQ Treap 一样分裂合并,同样支持文艺平衡树和可持久化。更重要的是,它的常数远远优于 FHQ Treap。缺点是节点数量为两倍,但是这能叫缺点吗?哪个数据结构题卡二倍空间。
好吧发现之前有一篇日报写过了,但是这篇文章会比那篇日报详尽很多,也会更深入探索 WBLT 的用法。此外他写的单旋时间复杂度应该是假的。
若没有特殊说明,文中的图片均为原创。
文章中所有代码的测试结果均在洛谷 C++14 (GCC 9) 环境下获得。
概述
Leafy 指将维护的信息记录在叶子节点上,与之对应的是 Nodey。
对于 Leafy Tree,它的叶子节点记录数列,非叶子节点记录左右儿子的值的较大值(由于左儿子的值一定不大于右儿子值,因此直接记录右儿子的值),节点数量为 2n-1 ,且非叶子节点的儿子数量均为 2 。
Leafy Tree 实现二叉搜索树
若依次将 inf 1 14 51 4 19 9 8 10 插入,可以得到这样的一棵树:
其中方点是叶子结点,圆点是非叶子结点。叶子节点的值排成了一个有序数列,非叶子节点上的值为右儿子的值。
利用 Leafy Tree 的性质,可以轻松地实现二叉搜索树。
下面的代码中尽量使用了非递归写法。即使要改成递归写法也是很容易的,而且没有本质上的区别。
当且仅当 siz_x = 1 时,节点 x 为叶节点。
规定 lp_x,rp_x 分别是 x 节点的左右儿子,val_x 表示 x 节点的值,siz_x 表示 x 子树内的叶子结点数量。
其中 siz_x,val_x 也可以这样定义:
否则,siz_x = siz_{lp_x} + siz_{rp_x}, val_x = val_{rp_x} 。
若不作说明,默认被操作数为 k 。
新建节点
无需说明。
il int newnode(int k) {
siz[++tot] = 1; val[tot] = k;
return tot;
}查找排名
首先记录一个 cnt ,初值为 0 。其含义为小于等于 k 的值的数量,需要在查询过程中进行累加。
当前节点不是叶子节点时,若 val_{lp_{now}} \geq k ,则 now \leftarrow lp_{now} ,即在左子树中查询 k 的排名。反之,则 now \leftarrow rp_{now} ,即在右子树中查询 k 的排名,同时 ,将 cnt 累加 siz_{lp_{now}} 。原理是找到第一个大于等于 k 的位置,而在这个过程中,val_{lp_{now}} \geq k 时,这个位置一定在左边,反之,这个位置一定在右边,并且左边的所有数都小于 k ,所以要累加计数器。
当前节点是叶子节点时,返回 cnt + 1 即为答案。
il int find_rnk(int k) {
int now = rt, cnt = 0;
while (true) {
if (siz[now] == 1) return cnt + 1;
else if (val[lp[now]] >= k) now = lp[now];
else cnt += siz[lp[now]], now = rp[now];
}
}查找第 k 小
当前节点不是叶子节点时,若 siz_{lp_{now}} \geq k ,则 now \leftarrow lp_{now} ,即在左子树中查询第 k 小。反之,则 k\leftarrow k-siz_{lp_{now}},now \leftarrow rp_{now} ,即在右子树中查询排除左边数量的第 k 小。
当前节点是叶子节点时,返回 val_{now} 即为答案。
il int find_kth(int k) {
int now = rt;
while (true) {
if (siz[now] == 1) return k == 1 ? val[now] : -1;
else if (siz[lp[now]] >= k) now = lp[now];
else k -= siz[lp[now]], now = rp[now];
}
}查找前驱
先找到 k 的排名 p ,输出第 p - 1 小。
il int find_pre(int k) {
return find_kth(find_rnk(k) - 1);
}查找后继
几乎一致,不再赘述。
il int find_suc(int k) {
return find_kth(find_rnk(k + 1));
}插入
当前节点不是叶子节点时,若 k \leq val_{lp_{now}} ,则将 k 插入左子树;反之插入右子树。
当前节点是叶子节点时,新建两个点 p, q 。让这两个点的值分别等于 val_{now} 和 k ,再钦定 val_p < val_q ,令 now 变为非叶子节点,其左儿子为 p ,右儿子为 q 。采用递归实现,注意回溯时要更新节点信息。
举个例子。把开头的数列拿过来。若已经将 inf 1 14 51 4 19 9 8 插入,现在插入 10 。首先沿着 val 找到红色叶子节点进行插入操作:
红色节点不再是叶子节点。新建点 p, q ,值为红色节点的值和 k ,再使 val_p < val_q ,分别作为红色节点的左右儿子。
il void pushup(int x) {
siz[x] = siz[lp[x]] + siz[rp[x]];
val[x] = val[rp[x]];
}
il void insert(int now, int k) {
if (siz[now] == 1) {
int p = newnode(val[now]), q = newnode(k);
if (val[p] > val[q]) swap(p, q);
lp[now] = p, rp[now] = q;
return pushup(now);
}
insert(k <= val[lp[now]] ? lp[now] : rp[now], k);
pushup(now);
}特殊地,初始时没有任何节点,此时使根节点 rt 等于插入的第一个元素即可。
为了避免各种边界,一般提前插入一个永远不会删除的数。否则可能出现树被删空的情况,增加冗余讨论。
rt = newnode(INT_MAX);除了第一个元素,每一次插入都会新建两个节点,因此一共有 2n - 1 个节点。
删除
这里保证被删数存在。
这里没有写垃圾回收,原因是大部分时候可以认为在删除操作上的垃圾回收没有意义。
理解了插入操作后,删除操作也很容易。找到了待删除的叶子结点后,将其父亲的属性均设为兄弟,然后删除该节点和其兄弟节点。
这里的实现是如果要删 now 的儿子,直接修改 now ,避免了记录父亲。
第一种实现:
il void delt(int now, int k) {
if (val[lp[now]] >= k) {
if (siz[lp[now]] == 1) {
val[now] = val[rp[now]]; siz[now] = siz[rp[now]];
lp[now] = lp[rp[now]]; rp[now] = rp[rp[now]];
} else delt(lp[now], k), pushup(now);
} else {
if (siz[rp[now]] == 1) {
val[now] = val[lp[now]]; siz[now] = siz[lp[now]];
rp[now] = rp[lp[now]]; lp[now] = lp[lp[now]];
} else delt(rp[now], k), pushup(now);
}
}这份 delete 有一些需要注意的点:
若修改后是叶子结点,不能 pushup。发现如果修改的是 now 的儿子,无需 pushup。综上,仅在回溯时 pushup。
赋值属性时,这里可以发现,如果删除左儿子,则先赋值左儿子,再赋值右儿子;反之,先赋值右儿子,再赋值左儿子。如果脑子累,可以用更巧妙的方式避免这个优先级问题——引用 。相当于直接把儿子的编号提上来,如下图:
例如在上面的树中删去 4 。首先找到该叶子节点及其父节点。
删除后剩下右儿子子树。
将原父节点的编号直接赋为右儿子的编号。
删除完成。
il void delt(int &now, int k) {
if (val[lp[now]] >= k) {
if (siz[lp[now]] == 1) now = rp[now];
else delt(lp[now], k), pushup(now);
} else {
if (siz[rp[now]] == 1) now = lp[now];
else delt(rp[now], k), pushup(now);
}
}两种实现的区别在于,第一种相当于分别更新左右子树的编号,而第二种是直接修改了子树根节点的编号。
这些操作可以轻松卡到单次 \mathcal O(n) ,总时间复杂度 \mathcal O(nq) 。
可以通过没有删除操作的 P5076,也可以尝试提交 P3369 验证删除的正确性。由于其优秀的常数和数据的水分,在 P3369 中可以获得 88 的好成绩。
附上完整的操作代码:
struct LEAFY {
int lp[MAXN], rp[MAXN], val[MAXN], siz[MAXN], tot;
int rt;
il void pushup(int x) {
siz[x] = siz[lp[x]] + siz[rp[x]];
val[x] = val[rp[x]];
}
il int newnode(int k) {
siz[++tot] = 1; val[tot] = k;
return tot;
}
il int find_rnk(int k) {
int now = rt, cnt = 0;
while (true) {
if (siz[now] == 1) return cnt + 1;
else if (val[lp[now]] >= k) now = lp[now];
else cnt += siz[lp[now]], now = rp[now];
}
}
il int find_kth(int k) {
int now = rt;
while (true) {
if (siz[now] == 1) return k == 1 ? val[now] : -1;
else if (siz[lp[now]] >= k) now = lp[now];
else k -= siz[lp[now]], now = rp[now];
}
}
il int find_pre(int k) {
return find_kth(find_rnk(k) - 1);
}
il int find_suc(int k) {
return find_kth(find_rnk(k + 1));
}
il void insert(int now, int k) {
if (siz[now] == 1) {
int p = newnode(val[now]), q = newnode(k);
if (val[p] > val[q]) swap(p, q);
lp[now] = p, rp[now] = q;
return pushup(now);
}
insert(k <= val[lp[now]] ? lp[now] : rp[now], k);
pushup(now);
}
il void delt(int &now, int k) {
if (val[lp[now]] >= k) {
if (siz[lp[now]] == 1) now = rp[now];
else delt(lp[now], k), pushup(now);
} else {
if (siz[rp[now]] == 1) now = lp[now];
else delt(rp[now], k), pushup(now);
}
}
} T;
int main() {
int q; read(q); T.rt = T.newnode(INT_MAX); T.insert(T.rt, INT_MIN + 1);
int op, x;
while (q--) {
read(op, x);
if (op == 1) T.insert(T.rt, x);
else if (op == 2) T.delt(T.rt, x);
else if (op == 3) printf("%d\n", T.find_rnk(x) - 1);
else if (op == 4) printf("%d\n", T.find_kth(x + 1));
else if (op == 5) printf("%d\n", T.find_pre(x));
else printf("%d\n", T.find_suc(x));
}
rout;
}Leafy Tree 实现加权平衡树
加权平衡树(Weight Balanced Tree),通过 Leafy Tree 实现即 Weight Balanced Leafy Tree(WBLT)。
定义一个节点的权重 weight_x=siz_x 。如果一个节点满足 \min\{weight_{lp_x}, weight_{rp_x}\}\geq \alpha \cdot weight_x ,则称这个节点是 \alpha 加权平衡的。显然 0<\alpha \leq \dfrac{1}{2} ,这里简单证一下:
设正整数 x\leq y ,满足 \min\{x, y\}\geq \alpha \cdot (x + y) ,则 x\geq \alpha\cdot(x+y) ,进而 \alpha\leq\dfrac{x}{x + y} 。显然 \dfrac{x}{x + y}\leq \dfrac{1}{2} ,则 \alpha \leq \dfrac{1}{2} 。
若一棵子树 T 的所有非叶子节点均满足 \alpha 加权平衡,则认为这棵子树是 \alpha 加权平衡的。
一棵含有 n 个元素的加权平衡树的高度 h 满足 h\leq \log_{\frac{1}{1-\alpha}} n=\mathcal O(\log n) 。
两个旋转图图源:论文
这里使用旋转维护加权平衡树的平衡。
当插入或删除一个节点后,树的形态发生变化。其中被影响到权重的点是一条链。考虑依次处理这些节点。
设这棵树的一个子树 T 中,除根节点外的所有节点均满足 \alpha 加权平衡。我们可以用一次单旋或双旋操作使 T 满足 \alpha 加权平衡。
定义一个节点 x 的平衡度为 \dfrac{weight_{lp_x}}{weight_x} 。
如图,设 x,y 旋转前的平衡度分别为 \rho_1,\rho_2 ,旋转后的平衡度分别为 \gamma_1,\gamma_2 。可以得到 \gamma_1=\dfrac{\rho_1}{\rho_1+\rho_2(1-\rho_1)},\gamma_2=\rho_1+\rho_2(1-\rho_1) 。论文中没有给出证明,自己胡了一个有点丑的推导过程。如果有更好的方法请不吝赐教。
注意这里的 weight_x 均表示旋转前的值。
先展开各式。
\begin{aligned}
\rho_1=\dfrac{weight_{lp_x}}{weight_{lp_x}+weight_{rp_x}}\Rightarrow weight_{lp_x}=\rho_1(weight_{lp_x} + weight_{rp_x})\\
\rho_2=\dfrac{weight_{lp_y}}{weight_{lp_y}+weight_{rp_y}}\Rightarrow weight_{lp_y}=\rho_2(weight_{lp_y} + weight_{rp_y})\\
\end{aligned}
由定义得
\gamma_1=\dfrac{weight_{lp_x}}{weight_{lp_x} + weight_{lp_y}}
代入 weight_{lp_x}, weight_{lp_y} 得
\begin{aligned}
\gamma_1&=\dfrac{\rho_1(weight_{lp_x} + weight_{rp_x})}{\rho_1(weight_{lp_x} + weight_{rp_x}) + \rho_2(weight_{lp_y} + weight_{rp_y})}\\
&=\dfrac{\rho_1}{\rho_1+\rho_2\frac{weight_{lp_y}+weight_{rp_y}}{weight_{lp_x}+weight_{rp_x}}}
\end{aligned}
观察旋转前图像得 weight_{lp_y}+weight_{rp_y}=weight_{rp_x} ,再次代入得
\begin{aligned}
\gamma_1&=\dfrac{\rho_1}{\rho_1+\rho_2\frac{weight_{rp_x}}{weight_{lp_x}+weight_{rp_x}}}\\
&=\dfrac{\rho_1}{\rho_1+\rho_2(1-\frac{weight_{lp_x}}{weight_{lp_x}+weight_{rp_x}})}\\
&=\dfrac{\rho_1}{\rho_1+\rho_2(1-\rho_1)}
\end{aligned}
由定义得
$$
\gamma_2=\dfrac{weight_{lp_x}+weight_{lp_y}}{weight_{lp_x} + weight_{lp_y} + weight_{rp_y}}
$$
由 $weight_{lp_y}+weight_{rp_y}=weight_{rp_x}$,代入得
$$
\begin{aligned}
\gamma_2&=\dfrac{weight_{lp_x}+weight_{lp_y}}{weight_{lp_x} + weight_{rp_x}}\\
&=\rho_1+\dfrac{weight_{lp_y}}{weight_{lp_x} + weight_{rp_x}}\\
&=\rho_1+\rho_2\dfrac{weight_{lp_y}+weight_{rp_y}}{weight_{lp_x} + weight_{rp_x}}\\
&=\rho_1+\rho_2\dfrac{weight_{rp_x}}{weight_{lp_x} + weight_{rp_x}}\\
&=\rho_1+\rho_2(1-\rho_1)
\end{aligned}
$$

如图,设 $x,y,z$ 旋转前的平衡度分别为 $\rho_1,\rho_2,\rho_3$,旋转后的平衡度分别为 $\gamma_1,\gamma_2,\gamma_3$。可以得到 $\gamma_1=\dfrac{\rho_1}{\rho_1+\rho_2\rho_3(1-\rho_1)},\gamma_2=\rho_1+\rho_2\rho_3(1-\rho_1),\gamma_3=\dfrac{\rho_2(1-\rho_3)}{1-\rho_2\rho_3}$。证明方法与单旋时类似,不再赘述。
可以证明当 $\alpha\leq 1-\frac{\sqrt 2}{2}$ 时,通过这两种操作,使得操作后的这些节点的平衡度在 $[\alpha,1-\alpha]$ 内。
当 $\rho_2 < \frac{1-2\alpha}{1-\alpha}$ 时,执行一次单旋,否则执行一次双旋。
------------------
下面在 $lp, rp$ 的同时定义左儿子是 $ch_0$,右儿子是 $ch_1$。
。。。旋转和维护平衡按照上面的规则写就好了。$\alpha$ 取 $1-\frac{\sqrt 2}{2}\approx 0.29$。nalemy 称取 $0.25$ 会更快,不过作者不太懂这方面的内容。
```cpp
il void rotate(int x, bool d) { // d 表示将哪个儿子旋转到 x 的位置
swap(lp[x], rp[x]);
swap(lp[ch(x, d ^ 1)], rp[ch(x, d ^ 1)]);
swap(ch(ch(x, d ^ 1), d ^ 1), ch(x, d));
pushup(ch(x, d ^ 1)); pushup(x);
}
il void maintain(int x) {
int d;
if (siz[x] == 1) return;
if (siz[lp[x]] < siz[x] * alpha) d = 1;
else if (siz[rp[x]] < siz[x] * alpha) d = 0;
else return;
if (siz[ch(ch(x, d), d ^ 1)] * (1 - alpha) >= siz[ch(x, d)] * (1 - 2 * alpha))
rotate(ch(x, d), d ^ 1);
rotate(x, d);
}
```
只需要在树的形态发生改变时——插入/删除后,对每一个回溯时的节点进行 maintain 操作维护平衡即可。其余操作显然与实现二叉搜索树的代码没有任何差异。
贴上更改后的插入删除代码。
```cpp
il void insert(int now, int k) {
if (siz[now] == 1) {
int p = newnode(val[now]), q = newnode(k);
if (val[p] > val[q]) swap(p, q);
lp[now] = p, rp[now] = q;
return pushup(now);
}
insert(k <= val[lp[now]] ? lp[now] : rp[now], k);
pushup(now); maintain(now);
}
il void delt(int &now, int k) {
if (val[lp[now]] >= k) {
if (siz[lp[now]] == 1) {
now = rp[now];
} else delt(lp[now], k), pushup(now), maintain(now);
} else {
if (siz[rp[now]] == 1) {
now = lp[now];
} else delt(rp[now], k), pushup(now), maintain(now);
}
}
```
时间复杂度 $\mathcal O(n\log n)$。在 [P6136](https://www.luogu.com.cn/problem/P6136) 中,WBLT 的常数优势体现得非常明显。稍有优化的 FHQ-Treap(即尽量不依靠分裂合并操作以减小常数)在 13.5s 左右,不优化的 FHQ-Treap 在 16s 左右,贺了一份旋转 Treap 在 12.5s 左右,[WBLT](https://www.luogu.com.cn/record/101211140) 在 8.5s 左右。
不过总时间的比较反而有些片面。若仔细对比每个测试点,会发现在一些测试点上 WBLT 对于 Treap 达到 $2\sim 4$ 倍的碾压;而相对来看,有些 WBLT 稍慢的测试点差距并不明显。
~~题外话:看来是否旋转的 Treap 效率差异并不明显啊。~~
@[DRPLANT](https://www.luogu.com.cn/user/111789) 提出有 [一种做法](https://www.luogu.com.cn/blog/user19567/treap-zen-yang-pao-dei-geng-kuai) 可以使 FHQ-Treap 的效率有进一步提升。
- 这里有 @[YamadaRyou](https://www.luogu.com.cn/user/203008) 的一份 [实现](https://www.luogu.com.cn/record/127353973)。
- 这里有 @[DRPLANT](https://www.luogu.com.cn/user/111789) 的一份 [实现](https://www.luogu.com.cn/paste/5g5ylrt4)。
目前两者均可以通过。
被卡了之后进行了一定探讨。考虑这种优化的实质是减少 split 和 merge 的无用操作。有相同权值的情况下,若 split 将相等的数放到左子树,那么插入时应放到右子树。
## 更进一步
### 合并
合并是指将两棵值域无交集的树联成一棵的操作,其中第一棵树的最大值不大于第二棵树的最小值。
假设合并两棵树 $A, B$。如果 $\min\{weight_{A}, weight_{B}\}\geq \alpha \cdot (weight_A + weight_B)$,那么新建一个节点,左右儿子分别是 $A,B$。这样直接合并起来就是平衡的。
对于其他的情况,现钦定 $siz_A\geq siz_B$。
- 若 $A$ 的左子树变为合并后的左子树足以达到平衡,递归合并。形式化的,若 $siz_{lp_A}\geq \alpha \cdot (weight_A + weight_B)$,将 $A$ 的左子树作为最终左子树,$A$ 的右子树与 $B$ 合并的结果作为最终右子树。
- 否则,将 $A$ 的左子树与 $A$ 的右子树的左子树合并的结果作为最终左子树,$A$ 的右子树的右子树与 $B$ 合并的结果作为最终右子树。
时间复杂度 $\mathcal O(\log \frac{\max\{siz_A,siz_B\}}{\min\{siz_A,siz_B\}})$,常数不小。记得垃圾回收,合并部分的垃圾回收也是众多博客忽略的一点,详见代码。如果一个节点此后不再使用它的信息,则可以回收。画画图可以更好地理解。
```cpp
il int merge(int x, int y) {
if (!x || !y) return x | y;
int tal = siz[x] + siz[y];
if (min(siz[x], siz[y]) >= alpha * tal) {
int t = newnode(0);
lp[t] = x, rp[t] = y;
return pushup(t), t;
}
if (siz[x] >= siz[y]) {
if (siz[lp[x]] >= alpha * tal) return rp[x] = merge(rp[x], y), pushup(x), x;
lp[x] = merge(lp[x], lp[rp[x]]);
int p = rp[x];
rp[x] = merge(rp[rp[x]], y);
st[++len] = p;
return pushup(x), x;
} else {
if (siz[rp[y]] >= alpha * tal) return lp[y] = merge(x, lp[y]), pushup(y), y;
rp[y] = merge(rp[lp[y]], rp[y]);
int p = lp[y];
lp[y] = merge(x, lp[lp[y]]);
st[++len] = p;
return pushup(y), y;
}
}
```
合并的讲解到此结束,可以跳过下面的这一段。
关于网上普遍流行的两种写法:
```cpp
il int merge(int x, int y) {
if (!x || !y) return x | y;
int t = newnode(0);
lp[t] = x, rp[t] = y;
pushup(t);
return t;
}
```
这是在扯淡,不题。
```cpp
il int merge(int x, int y) {
if (!x || !y) return x | y;
int t = newnode(0);
lp[t] = x, rp[t] = y;
pushup(t); maintain(t);
return t;
}
```
看起来很有道理,甚至我也以为它是对的。但是考虑这样的情况:
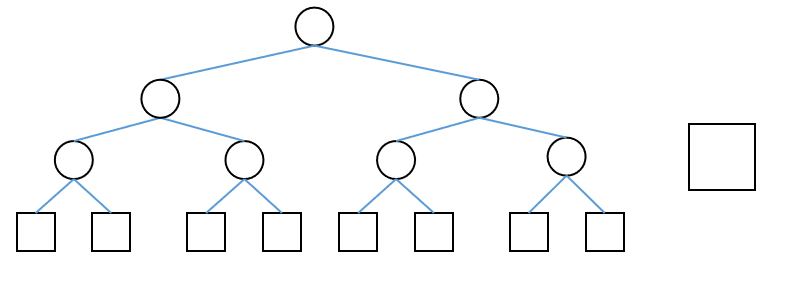
左边是一棵满二叉树,右边是一个节点。直接合并后维护“平衡”,却得到了这样的结果:
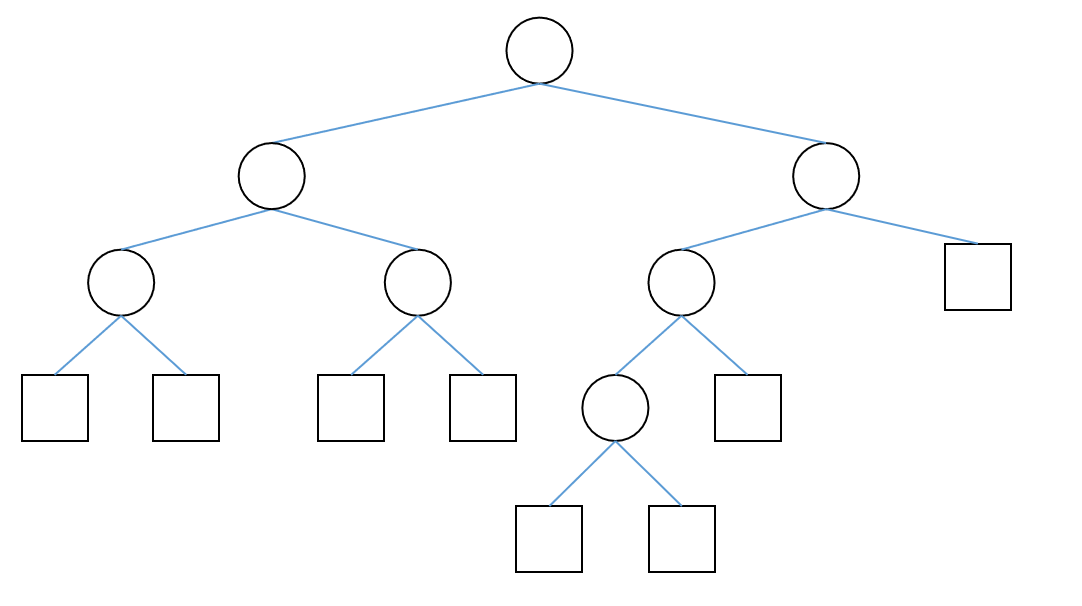
很遗憾,它并不满足 $\alpha$ 加权平衡。这样错误合并次数太多之后,时间复杂度会遭到毁灭性的打击。
**但是,我还有一些想法。**
论文中写到,
>假设这棵树的一个子树 $T$ 中,除根节点外的所有节点均满足 $\alpha$ 加权平衡。我们可以用
一次单旋或双旋操作使 $T$ 满足 $\alpha$ 加权平衡。
我认为这里出现问题的原因就是一棵“子树”内只有叶节点。因此当出现某棵树的节点数量为 $1$ 时,执行普通的插入操作。这样写之后是能通过模板的,但是没得到证实。
upd:过不了加强版。
```cpp
il int merge(int x, int y) {
if (!x || !y) return x | y;
if (siz[x] == 1) {
insert(y, val[x]); st[++len] = x;
return y;
}
if (siz[y] == 1) {
insert(x, val[y]); st[++len] = y;
return x;
}
int t = newnode(0);
lp[t] = x, rp[t] = y;
pushup(t); maintain(t);
return t;
}
```
### 分裂
与 FHQ-Treap 类似,注意终止条件是叶节点。
**但是不能写成 FHQ-Treap 那样。原因是 merge 的要求是两棵树分别满足 $\alpha$ 加权平衡,若按 FHQ-Treap 的写法分裂,无法保证分裂出来的两棵树一定满足这个条件。**
1. 按权值分裂
按权值分裂指将小于等于 $k$ 的叶节点放到一棵树中,其余的放到一棵树中。
首先要有两个根节点 $x,y$。从 $now$ 一路向下走,若 $k\geq val_{lp_{now}}$,那么左儿子可以全部并入 $x$,递归分裂右儿子;反之, 右儿子可以全部并入 $y$,递归分裂左儿子。注意垃圾回收。
```cpp
il void split(int now, int k, int &x, int &y) {
if (siz[now] == 1) {
if (val[now] <= k) x = now, y = 0;
else x = 0, y = now;
return;
}
if (k >= val[lp[now]]) {
split(rp[now], k, x, y);
x = merge(lp[now], x); st[++len] = now;
} else {
split(lp[now], k, x, y);
y = merge(y, rp[now]); st[++len] = now;
}
}
```
2. 按排名分裂
按排名分裂指将前 $k$ 个叶节点放到一棵树中,其余的放到一棵树中。
与按权值分裂类似,不过可以加一个小边界剪枝。记得垃圾回收。
```cpp
il void split(int now, int k, int &x, int &y) {
if (!k) return x = 0, y = now, void();
if (siz[now] == 1) return x = now, y = 0, void();
if (k >= siz[lp[now]]) {
split(rp[now], k - siz[lp[now]], x, y);
x = merge(lp[now], x); st[++len] = now;
} else {
split(lp[now], k, x, y);
y = merge(y, rp[now]); st[++len] = now;
}
}
```
分裂的时间复杂度为 $\mathcal O(\log n)$。
**分裂合并操作一定要记得垃圾回收!** 不然这个 WBLT 放在评测机里遇毒瘤数据变大变高,浪费节点很强的,空间复杂度长成了 $\mathcal O(t\log n)$,其中 $t$ 是操作次数。
垃圾回收后由于会有一次操作的回收不及时,所以空间需要开 $2n + \log_{\frac{1}{1-\alpha}} n$,别开小了。
### 文艺平衡树
WBLT 显然是支持文艺平衡树的。
类型一:[P4036 火星人](https://www.luogu.com.cn/problem/P4036)
字符串哈希之后,可以二分 LCQ 的长度,每一次在平衡树上查询哈希值判断即可。
WBLT 如何维护哈希值?
- 首先需要在 pushup 的部分更新该节点哈希值。显然有 $h_x=h_{lp_x}\times base^{siz_{rp_x}}+h_{rp_x}$,其中 $base$ 是哈希时自选的底数。
- 对于修改操作,找到对应的节点直接修改即可。
- 对于插入操作,找到对应的节点后,与普通的方式类似,不过这里插入在第 $k$ 个位置之后对应在平衡树上就是让新插入的节点是右儿子。
- 对于查询,只需要分裂出查询的区间得到答案,再合并回去。
详细可以看看代码,还是挺好理解的。其常数仍然比较优秀。
```cpp
ull pw[MAXN]; char s[MAXN];
struct LEAFY {
int lp[MAXN], rp[MAXN], siz[MAXN], tot;
int st[MAXN], len;
int rt, x, y, z; const double alpha = 0.29;
ull has[MAXN];
#define ch(x, d) ((d) ? rp[x] : lp[x])
il void pushup(int x) {
siz[x] = siz[lp[x]] + siz[rp[x]];
has[x] = has[lp[x]] * pw[siz[rp[x]]] + has[rp[x]];
}
il int newnode(int k) {
int p = len ? st[len--] : ++tot;
siz[p] = 1; has[p] = k; lp[p] = rp[p] = 0;
return p;
}
il void rotate(int x, bool d) {
swap(lp[x], rp[x]);
swap(lp[ch(x, d ^ 1)], rp[ch(x, d ^ 1)]);
swap(ch(ch(x, d ^ 1), d ^ 1), ch(x, d));
pushup(ch(x, d ^ 1)); pushup(x);
}
il void maintain(int x) {
int d;
if (siz[x] == 1) return;
if (siz[lp[x]] < siz[x] * alpha) d = 1;
else if (siz[rp[x]] < siz[x] * alpha) d = 0;
else return;
if (siz[ch(ch(x, d), d ^ 1)] * (1 - alpha) >= siz[ch(x, d)] * (1 - 2 * alpha)) rotate(ch(x, d), d ^ 1);
rotate(x, d);
}
il int merge(int x, int y) {
if (!x || !y) return x | y;
int tal = siz[x] + siz[y];
if (min(siz[x], siz[y]) >= alpha * tal) {
int t = newnode(0);
lp[t] = x, rp[t] = y;
return pushup(t), t;
}
if (siz[x] >= siz[y]) {
if (siz[lp[x]] >= alpha * tal) return rp[x] = merge(rp[x], y), pushup(x), x;
lp[x] = merge(lp[x], lp[rp[x]]);
int p = rp[x];
rp[x] = merge(rp[rp[x]], y);
st[++len] = p;
return pushup(x), x;
} else {
if (siz[rp[y]] >= alpha * tal) return lp[y] = merge(x, lp[y]), pushup(y), y;
rp[y] = merge(rp[lp[y]], rp[y]);
int p = lp[y];
lp[y] = merge(x, lp[lp[y]]);
st[++len] = p;
return pushup(y), y;
}
}
il void split(int now, int k, int &x, int &y) {
if (!k) return x = 0, y = now, void();
if (siz[now] == 1) return x = now, y = 0, void();
if (k >= siz[lp[now]]) {
split(rp[now], k - siz[lp[now]], x, y);
x = merge(lp[now], x); st[++len] = now;
} else {
split(lp[now], k, x, y);
y = merge(y, rp[now]); st[++len] = now;
}
}
il void insert(int now, int k, int ch) { // 插到第 k 个位置之后
if (siz[now] == 1) {
int p = newnode(has[now]), q = newnode(ch);
lp[now] = p, rp[now] = q;
return pushup(now);
}
if (siz[lp[now]] >= k) insert(lp[now], k, ch);
else insert(rp[now], k - siz[lp[now]], ch);
pushup(now); maintain(now);
}
il void update(int now, int k, int ch) {
if (siz[now] == 1) {
has[now] = ch;
return;
}
if (siz[lp[now]] >= k) update(lp[now], k, ch);
else update(rp[now], k - siz[lp[now]], ch);
pushup(now); maintain(now);
}
il ull query(int l, int r) {
int t1, t2, t3, t4;
split(rt, l - 1, t1, t2); split(t2, r - l + 1, t3, t4);
ull ans = has[t3];
return rt = merge(t1, merge(t3, t4)), ans;
}
} T;
int main() {
T.rt = T.newnode(27); T.insert(T.rt, 1, 28);
scanf("%s", s + 1); int n = strlen(s + 1), m; pw[0] = 1;
rep1(i, 1, 2e5) pw[i] = pw[i - 1] * 131;
rep1(i, 1, n) T.insert(T.rt, i, s[i] - 'a' + 1);
read(m); char op; int x, y; char d;
while (m--) {
scanf(" %c", &op); read(x);
if (op == 'Q') {
read(y);
int l = 0, r = T.siz[T.rt] - 2 - max(x, y) + 1;
while (l ^ r) {
int mid = l + r + 1 >> 1;
if (T.query(x + 1, x + mid) == T.query(y + 1, y + mid)) l = mid;
else r = mid - 1;
} printf("%d\n", l);
} else if (op == 'R') scanf(" %c", &d), T.update(T.rt, x + 1, d - 'a' + 1);
else scanf(" %c", &d), T.insert(T.rt, x + 1, d - 'a' + 1);
}
rout;
}
```
类型二:[【模板】文艺平衡树](https://www.luogu.com.cn/problem/P3391)
这道题目需要下传懒标记。将要修改的区间分裂出来打上翻转标记,并交换左右子树。下传标记的时机是当需要使用/进入某个节点的左/右子树时,下传标记。
输出时中序遍历输出叶节点即可。
由于此题初始的元素是给定的,可以在最开始用类似线段树的方式 $\mathcal O(n)$ 建树,这样是最平衡的。上一道题也可以这样。
```cpp
int n, m;
struct LEAFY {
int lp[MAXN], rp[MAXN], siz[MAXN], val[MAXN], tag[MAXN], tot;
int st[MAXN], len;
int rt, x, y, z; const double alpha = 0.29;
#define ch(x, d) ((d) ? rp[x] : lp[x])
il void pushup(int x) {
siz[x] = siz[lp[x]] + siz[rp[x]];
}
il void pushdown(int x) {
if (!tag[x]) return;
tag[lp[x]] ^= 1; tag[rp[x]] ^= 1;
swap(lp[lp[x]], rp[lp[x]]); swap(lp[rp[x]], rp[rp[x]]);
tag[x] = 0;
}
il int newnode() {
int p = len ? st[len--] : ++tot;
siz[p] = 1; lp[p] = rp[p] = 0;
return p;
}
il void build(int &x, int l, int r) {
x = newnode();
if (l == r) return val[x] = l, void();
int mid = l + r >> 1;
build(lp[x], l, mid); build(rp[x], mid + 1, r);
pushup(x);
}
il int merge(int x, int y) {
if (!x || !y) return x | y;
int tal = siz[x] + siz[y];
if (min(siz[x], siz[y]) >= alpha * tal) {
int t = newnode();
lp[t] = x, rp[t] = y;
return pushup(t), t;
}
if (siz[x] >= siz[y]) {
pushdown(x);
if (siz[lp[x]] >= alpha * tal) return rp[x] = merge(rp[x], y), pushup(x), x;
lp[x] = merge(lp[x], lp[rp[x]]);
pushdown(rp[x]);
int p = rp[x];
rp[x] = merge(rp[rp[x]], y); st[++len] = p;
return pushup(x), x;
} else {
pushdown(y);
if (siz[rp[y]] >= alpha * tal) return lp[y] = merge(x, lp[y]), pushup(y), y;
rp[y] = merge(rp[lp[y]], rp[y]);
pushdown(lp[y]);
int p = lp[y];
lp[y] = merge(x, lp[lp[y]]); st[++len] = p;
return pushup(y), y;
}
}
il void split(int now, int k, int &x, int &y) {
if (!k) return x = 0, y = now, void();
if (siz[now] == 1) return x = now, y = 0, void();
pushdown(now);
if (k >= siz[lp[now]]) {
split(rp[now], k - siz[lp[now]], x, y);
x = merge(lp[now], x); st[++len] = now;
} else {
split(lp[now], k, x, y);
y = merge(y, rp[now]); st[++len] = now;
}
}
il void update(int l, int r) {
int t1, t2, t3, t4;
split(rt, l - 1, t1, t2); split(t2, r - l + 1, t3, t4);
tag[t3] ^= 1; swap(lp[t3], rp[t3]);
rt = merge(t1, merge(t3, t4));
}
il void print(int x) {
if (siz[x] == 1) return printf("%d ", val[x]), void();
pushdown(x);
print(lp[x]); print(rp[x]);
}
} T;
int main() {
read(n, m);
T.build(T.rt, 1, n);
int l, r;
while (m--) read(l, r), T.update(l, r);
T.print(T.rt);
rout;
}
```
### 树套树
题目:[P3380](https://www.luogu.com.cn/problem/P3380)
事实上并不需要单独拿出来讲,毕竟思想都是一样的,只是用 WBLT 来完成平衡树的操作。不过翻了一下题解也没看到有人写 WBLT,所以这里也来写一份。
当然,这里仍然会比较详细地讲述整个思路及过程。作为一种大力数据结构,思想也是比较简单的。
假想一棵线段树,每一个节点上建立一棵平衡树。代表线段 $[l, r]$ 的节点上的平衡树中,插入 $a_l\sim a_r$。由于每个 $i$ 只会被 $\mathcal O(\log n)$ 个节点包含(因为深度是 $\mathcal O(\log n)$),所以每个位置会被插入到 $\mathcal O(\log n)$ 个线段中。
那么这些操作都很容易维护:
- 查询区间 $[l, r]$ 内 $k$ 的排名
将线段树上拼成 $[l, r]$ 的节点都找出来,对于每棵平衡树,查询小于 $k$ 的数的数量。累加起来再加一就是答案。
- $a_x\leftarrow y
该操作可以转化为:
在所有包含点 x 的线段上的平衡树中,删除 a_x 。
在所有包含点 x 的线段上的平衡树中,插入 y 。
将线段树上拼成 [l, r] 的节点都找出来,对于每棵平衡树,查询 k 的前驱,全部取 \max 就是答案。
将线段树上拼成 [l, r] 的节点都找出来,对于每棵平衡树,查询 k 的后继,全部取 \min 就是答案。
这个问题是线段树套平衡树的劣势。
这个问题可以转化为:找到一个最小的 x ,使得区间内小于等于 x + 1 的数的数量大于等于 k 。
如果不理解,回顾一下定义:第 k 小的数满足小于它的数有 k - 1 个。
这个问题显然可以二分。
除了最后一个操作,其他操作的时间复杂度为 \mathcal O(\log^2n) 。最后一个操作由于多了一个二分,时间复杂度为 \mathcal O(\log^2n \log v) 。
注意在写 WBLT 时,仍然要注意对于一些查询排名的操作,是否需要排除提前插入的 -\inf 。
目前这份代码需要开 O2 才能通过,不过也没找到可以不开 O2 通过此题的线段树套平衡树呢。尽管如此,它的常数已经十分优异,不开 O2 也可以在 2.20s 之内跑出结果,超越了极大部分其他平衡树。
与经典做法(树状数组套权值线段树)的比较:
经典做法空间复杂度为 \mathcal O(n\log n\log v) ,时间复杂度为 \mathcal O(n\log^2 n) 。
该做法空间复杂度为 \mathcal O(n\log n) ,时间复杂度为 \mathcal O(n\log^2 n\log v) 。虽然这在大部分情况下是一个较松的上界,但是洛谷数据太毒瘤了 QWQ,LOJ 上不开 O2 都能跑进 1s。
可以根据实际情况选取更合适的算法。
const int M = 4e6 + 50, N = 2e5 + 10;
int n, m, a[N];
struct LEAFY {
int lp[M], rp[M], val[M], siz[M], tot;
int st[M], len;
int rt[N], x, y; const double alpha = 0.29;
#define ch(x, d) ((d) ? rp[x] : lp[x])
il void pushup(int x) {
siz[x] = siz[lp[x]] + siz[rp[x]];
val[x] = val[rp[x]];
}
il int newnode(int k) {
int p = len ? st[len--] : ++tot;
siz[p] = 1; val[p] = k; lp[p] = rp[p] = 0;
return p;
}
il int find_rnk(int rt, int k) {
int now = rt, cnt = 0;
while (true) {
if (siz[now] == 1) return cnt + 1;
else if (val[lp[now]] >= k) now = lp[now];
else cnt += siz[lp[now]], now = rp[now];
}
}
il int find_kth(int rt, int k) {
int now = rt;
while (true) {
if (siz[now] == 1) return k == 1 ? val[now] : -1;
else if (siz[lp[now]] >= k) now = lp[now];
else k -= siz[lp[now]], now = rp[now];
}
}
il int find_pre(int rt, int k) {
return find_kth(rt, find_rnk(rt, k) - 1);
}
il int find_suc(int rt, int k) {
return find_kth(rt, find_rnk(rt, k + 1));
}
il void rotate(int x, bool d) {
swap(lp[x], rp[x]);
swap(lp[ch(x, d ^ 1)], rp[ch(x, d ^ 1)]);
swap(ch(ch(x, d ^ 1), d ^ 1), ch(x, d));
pushup(ch(x, d ^ 1)); pushup(x);
}
il void maintain(int x) {
int d;
if (siz[x] == 1) return;
if (siz[lp[x]] < siz[x] * alpha) d = 1;
else if (siz[rp[x]] < siz[x] * alpha) d = 0;
else return;
if (siz[ch(ch(x, d), d ^ 1)] * (1 - alpha) >= siz[ch(x, d)] * (1 - 2 * alpha)) rotate(ch(x, d), d ^ 1);
rotate(x, d);
}
il void insert(int &now, int k) {
if (siz[now] == 1) {
int p = newnode(val[now]), q = newnode(k);
if (val[p] > val[q]) swap(p, q);
lp[now] = p, rp[now] = q;
return pushup(now);
}
insert(k <= val[lp[now]] ? lp[now] : rp[now], k);
pushup(now); maintain(now);
}
il void delt(int &now, int k) {
if (val[lp[now]] >= k) {
if (siz[lp[now]] == 1) now = rp[now];
else delt(lp[now], k), pushup(now), maintain(now);
} else {
if (siz[rp[now]] == 1) now = lp[now];
else delt(rp[now], k), pushup(now), maintain(now);
}
}
} T;
il void insert(int x, int l, int r, int k, int v) {
if (!T.rt[x]) T.rt[x] = T.newnode(INT_MAX), T.insert(T.rt[x], INT_MIN + 1); // 由于这时候是空树,所以插入“哨兵值”。其余操作中树一定非空。
T.insert(T.rt[x], v);
if (l == r) return;
int mid = l + r >> 1;
if (k <= mid) insert(ls(x), l, mid, k, v);
else insert(rs(x), mid + 1, r, k, v);
}
il void update(int x, int l, int r, int k, int v1, int v2) {
T.delt(T.rt[x], v1); T.insert(T.rt[x], v2);
if (l == r) return;
int mid = l + r >> 1;
if (k <= mid) update(ls(x), l, mid, k, v1, v2);
else update(rs(x), mid + 1, r, k, v1, v2);
}
il int find_less_than(int x, int l, int r, int ql, int qr, int k) {
if (l > qr || r < ql) return 0;
if (l >= ql && r <= qr) return T.find_rnk(T.rt[x], k) - 2;
int mid = l + r >> 1;
return find_less_than(ls(x), l, mid, ql, qr, k) + find_less_than(rs(x), mid + 1, r, ql, qr, k);
}
il int find_pre(int x, int l, int r, int ql, int qr, int k) {
if (l > qr || r < ql) return INT_MIN + 1;
if (l >= ql && r <= qr) return T.find_pre(T.rt[x], k);
int mid = l + r >> 1;
return max(find_pre(ls(x), l, mid, ql, qr, k), find_pre(rs(x), mid + 1, r, ql, qr, k));
}
il int find_suc(int x, int l, int r, int ql, int qr, int k) {
if (l > qr || r < ql) return INT_MAX;
if (l >= ql && r <= qr) return T.find_suc(T.rt[x], k);
int mid = l + r >> 1;
return min(find_suc(ls(x), l, mid, ql, qr, k), find_suc(rs(x), mid + 1, r, ql, qr, k));
}
il int find_kth(int ql, int qr, int k) {
int l = 0, r = 1e8 + 1;
while (l ^ r) {
int mid = l + r >> 1;
if (find_less_than(1, 1, n, ql, qr, mid + 1) >= k) r = mid;
else l = mid + 1;
} return l;
}
int main() {
read(n, m); rer(i, 1, n, a);
rep1(i, 1, n) insert(1, 1, n, i, a[i]);
int op, x, y, z;
while (m--) {
read(op, x, y);
if (op == 1) printf("%d\n", find_less_than(1, 1, n, x, y, read()) + 1);
else if (op == 2) printf("%d\n", find_kth(x, y, read()));
else if (op == 3) update(1, 1, n, x, a[x], y), a[x] = y;
else if (op == 4) printf("%d\n", find_pre(1, 1, n, x, y, read()));
else printf("%d\n", find_suc(1, 1, n, x, y, read()));
}
rout;
}后记
由于资料的匮乏,许多地方都是我自行思考得出的,也因此可能出现谬误,感谢各位指出。
目前感觉 WBLT 并不被大家熟知,但它的确是一种不错的平衡树,也因此有不少错误写法并不会被卡。这篇文章也是希望这种数据结构不要埋没在茫茫大海中了。
这里应该出现 lxl,所以放一道 无关的题目,讲述了 lxl 与 WBLT 的故事。
作者还有很多事要忙,有一定概率回来更新可持久化的内容。 作者暂时放弃了。
参考资料:
王思齐 《Leafy Tree 及其实现的加权平衡树》
leafy tree和WBLT 学习笔记 - qwaszx 的博客
感谢洛谷上广大巨佬的帮助。
@DRPLANT 提供的有关 FHQ 的博客。
@YamadaRyou 对于这种 FHQ 写法的 代码实现。FHQ 的容易理解和容易实现仍然是毋庸置疑的优势,因此也同时在这里宣传一下这种做法。
以上两位大佬在代码被卡时提供的深刻帮助!
有问题在下面留言就行,我会尽力解答。