题解 CF1336E2 【Chiori and Doll Picking (hard version)】
memset0
·
·
题解
更好的阅读体验:https://memset0.cn/cf1336e2
这篇题解是出题人把刀架在我脖子上写的,锅了不关我事(雾
给定 n 个整数 \langle a_1, a_2 ... a_n \rangle,在 [0; 2^m) 的范围内。对于 k \in [0; m],求选出一个子集使得异或和的二进制表示有 k 个 1 的方案数。
---
## 0x00
做题之前,最重要的:
**当然是膜此题出题人 Sooke 大神**!
## 0x01
定义:
- $\operatorname{popcount}(x)$ 表示 $x$ 的二进制表示下 $1$ 的个数
- $\langle i, j \rangle = \operatorname{popcount(i \& j)}
对于线性基 S,定义:
-
-
F(S) = \sum_{x \in \operatorname{span}(S)} z^x
-
P(S) = \sum_{x \in \operatorname{span}(S)} z^{\operatorname{popcount}(x)}
对于此题,定义
首先你已经会了一个 O(2^{\operatorname{rank}(A)}) 的暴力,下文我们介绍一种 O(2^{m-\operatorname{rank}(A)}) 的算法,就可以通过分治在 O(2^{m/2}) 的时间复杂度内通过本题。
0x02
由线性基的基本性质,可以得到:
(z^x) * F(A) = F(A)
在此基础上枚举 x \in \operatorname{span}(A) 有
\begin{aligned}
F(A) * F(A) &= F(A) \cdot 2^{\operatorname{rank}(A)} \\
\operatorname{FWT}(F(A)) \cdot \operatorname{FWT}(F(A)) &= \operatorname{FWT}(F(A)) \cdot 2^{\operatorname{rank}(A)}
\end{aligned}
由于是按位相乘,考虑方程 x^2=x+1 的实根仅有 \left\{ \begin{aligned} x_1 &= 0 \\ x_2 &= 2^{\operatorname{rank}(A)} \end{aligned} \right.,故 [z^i] \operatorname{FWT}(F(A)) \in \{0, 2^{\operatorname{rank}(A)}\}。
0x03
让我们再回到 \operatorname{FWT} 运算本身的意义:
\begin{aligned}
[z^i] \operatorname{FWT}(F(A))
&= \sum_{x \in \operatorname{span}(A)} (-1)^{\langle i,x \rangle} \\
&\in \{ 0, 2^{\operatorname{rank}(A)} \} \\
\end{aligned}
如果存在 x 使得 (-1)^{\langle i,x \rangle} = -1,则 \operatorname{FWT}(A)_i 只能为 0。
$$
\langle i,x \rangle \oplus \langle j,x \rangle = \langle i \oplus j, x \rangle
$$
可以通过把 $\&$ 理解为二进制按位乘法,$\oplus$ 理解为二进制不进位加法来证明。
故我们只需检验 $A$ 中的每个基底而非 $\operatorname{span}(A)$ 即可判断这一位的值。
## 0x04
定义 $A$ 的正交线性基为 $B$,使得对于所有 $x \in \operatorname{span}(A), y \in \operatorname{span}(B)$,满足 $\operatorname{popcount(x \& y)}$ 是偶数,且 $\operatorname{rank}(A) + \operatorname{rank}(B) = m$。
根据前面的引理,有
$$
B \cdot 2^{\operatorname{rank}(A)} = \operatorname{FWT} (A) \Leftrightarrow \operatorname{IFWT}(B \cdot 2^{\operatorname{rank}(A)}) = A
$$
一种简单的正交线性基构造方式是
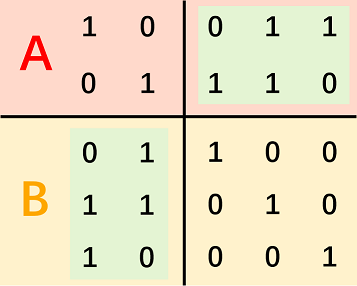
用高斯消元整理关键位,旋转右上角到左下角得到。
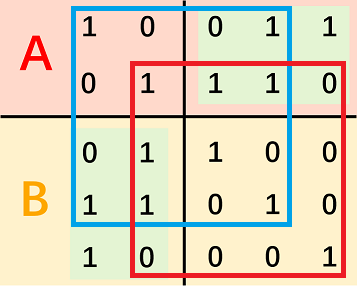
证明可以考虑图中圈出矩形的左上角和右上角一定为 $1$,而两向量的异或的 $\operatorname{popcount}$ 为偶数,那么左下角和右上角的数要么全为 $0$,要么全为 $1$。
## 0x05
知道了正交线性基怎么求,如何计算答案呢?
考虑用 $\operatorname{FWT}$ 表示答案统计:
$$
[z^c]P(A) = [z^0] (A * G^c) = [z^0] \operatorname{IFWT}(\operatorname{FWT}(F(A)) \cdot \operatorname{FWT}(G^c))
$$
其中 $G^c$ 表示 $\sum_{x \geq 0} z^x [\operatorname{popcount}(x)=c]$。
其中:
$$
[z^0] \operatorname{IFWT}(X) = 2^{-m} [z^0] \operatorname{FWT}(X) = 2^{-m} \sum_{i \geq 0} [z^i] X
$$
由于 $\operatorname{FWT}(F(A)) = F(B) \cdot 2^k$,而 $B$ 中的元素只有 $2^{\operatorname{rank}(B)} = 2^{m - \operatorname{rank}(A)}$ 个。故通过暴力得到 $P(B)$,即可通过组合数计算得 $P(A)$。
$$
[z^c]P(A) = 2^{k-m} \sum_{d \geq 0} [z^d] P(B) \sum_{i \geq 0} (-1)^i \binom d i \binom {m-d} {c-i}
$$