题解 CF348D Turtles
pigstd
·
·
题解
同步更新于 题目总结。
CF348D Turtles 容斥 dp,经典题。
首先考虑只有一只乌龟的时候怎么做,
这就是一个经典的 dp 问题,设 f_{i,j} 表示点 (1,1) 到 (i,j) 的方案数,a_{i,j} 表示 (i,j) 是否可走,那么有不难有:
然而题目让我们求的是两条不相交的路径,这个怎么求呢?
我们不难注意到,不相交的路径必然是一条 $(1,2) \to (n-1,m)$ 的路径和一条 $(2,1) \to (n,m-1)$ 的路径,而一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 必然是相交的。那么我们因为我们能求助所有 $(1,2) \to (n-1,m)$ 的路径和 $(2,1) \to (n,m-1)$ 的路径,那么我们只要减去满足上述条件,并且相交的路径总数就可以了。
对于两条有交点的路径,不妨在最后一个交点处,交换剩下的两个路径。那么这就转换成了一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 的路径。并且不难发现,这些路径是一一对应的。所以相交的路径总数就是一条 $(1,2) \to (n,m-1)$ 和一条 $(2,1) \to (n-1,m)$ 的路径总数。
画几幅图可能更容易理解:如果原来的两条相交的路径是这样的:
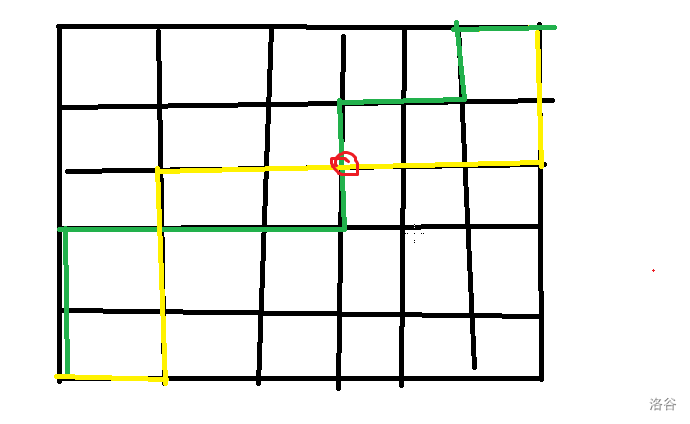
其中黄线和绿线分别表示两条路径,红圈表示最后一个交点处。那么可以讲此图转换成:
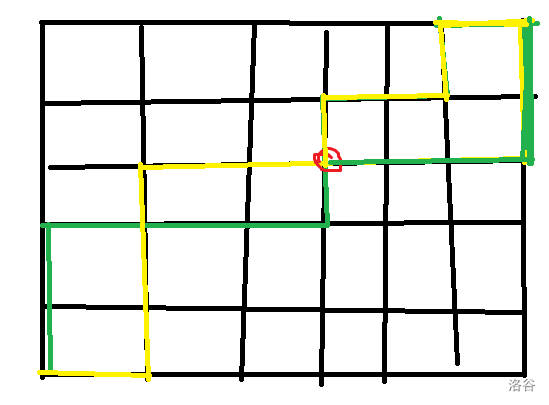
这样就是满足第二个条件的路径了。同理,每个满足第二个条件的两条路径也能够转化回来。
然后就转换成上述的经典问题了。设 $F(x1,y1,x2,y2)$ 表示 $(x1,y1) \to (x2,y2)$ 的路径总数,那么有 $ans=F(1,2,n-1,m)\times F(2,1,n,m-1)-F(1,2,n,m-1)\times F(2,1,n-1,m)$。时间复杂度 $O(n^2)$。
(吐槽:用 `string` 和 `cin` 读入字符串会被卡常)。
```cpp
#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
inline int read()
{
char c=getchar();int x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;return x;
}
const int Mod=1e9+7;
const int M=3010;
int f[M][M][4],n,m;
bool a[M][M];
int F(int x1,int y1,int x2,int y2,int tt)
{
// for (int i=1;i<=n;i++)for (int j=1;j<=m;j++)f[i][j]=0;
f[x1][y1][tt]=1;
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
if (a[i][j]==0)f[i][j][tt]=0;
else f[i][j][tt]=((f[i][j][tt]+f[i-1][j][tt])%Mod+f[i][j-1][tt])%Mod;
return f[x2][y2][tt];
}
char s[M];
signed main()
{
n=read(),m=read();
for (int i=1;i<=n;i++)
{
for (int j=1;j<=m;j++)
a[i][j]=(getchar()=='#'?0:1);
getchar();
}
long long ans=1ll*F(1,2,n-1,m,0)*F(2,1,n,m-1,1)-1ll*F(1,2,n,m-1,2)*F(2,1,n-1,m,3);
ans%=Mod,ans+=Mod,ans%=Mod;cout<<ans<<endl;
return 0;
}
```