题解 P4727 【[HNOI2009]图的同构计数】

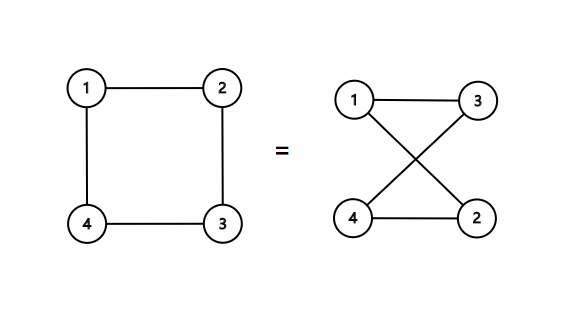
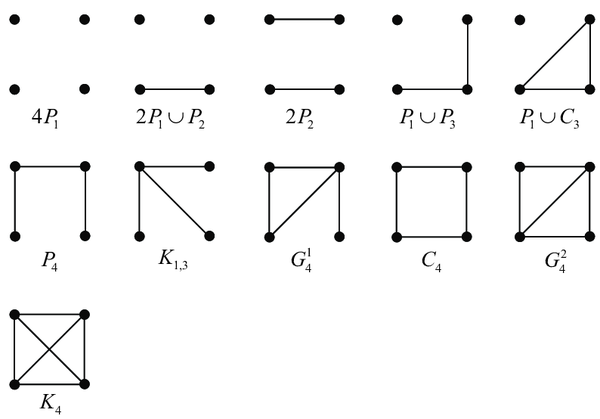
转自我在知乎上写的文章，可以看一看呀：[https://zhuanlan.zhihu.com/p/347566986](https://zhuanlan.zhihu.com/p/347566986) --- $$\,$$ $$\Large{1,2,4,11,34,156,1044\cdots}$$ $$\,$$ $\color{red}{\sf Part. 1}$ 在欣赏一个有趣的数列前，我们需要引入一个图论概念：**同构**。 $A,B$ 两图同构的意思是：$A$ 图的顶点可以经过一定的重新标号，使得它的点集和边集与 $B$ 相同。 例如，以下两个图是同构的：  因为如果将左图的 (3,4) 两点交换，两图的点集和边集是相等的。 再如，对于有 $4$ 个顶点的简单无向图，共有 $11$ 种互不同构的图：  #### 现在问题来了： $n$ 个顶点组成的简单无向图中，有多少种图互不同构？ 这个问题的答案便是文章开头的数列——[A000088](https://oeis.org/A000088)。 $$\,$$ $\color{red}{\sf Part.2}$ 为了解决这个问题，我们需要求助于数学的另一领域：群论。 将图的顶点重新标号，就相当于对点集进行置换，所有的标号方式便构成了一个置换群 $G$ 。我们要求的即是在 $G$ 作用下本质不同的图的个数。对于有 $n$ 个顶点的图，所有的标号方式便是顶点的全排列，即 $|G|=n!$ 。 现在隆重请出 ${\rm Burnside}$ 引理： $$|X/G|=\frac{1}{|G|}\sum_{g\in G}|X^g|$$ $|X/G|$ ：集合 $X$ 在群 $G$ 作用下的轨道数（或本质不同元素数） $|X^g|$ ：在变换 $g$ 下，$X$ 集合中的不动点数 这个定理对解决计数问题有重要作用，举个例子：  在本题中，$X$ 即为 $n$ 个顶点可以构成的 $2^{n(n-1)/2}$ 个简单无向图的集合，$|X/G|$ 即为所求。难点在于怎么求 $|X^g|$，**即对于某个点集置换 $g$ 而言，有多少张图在经历变换 $g$ 后依然和原来的图相同**？ $$\,$$ $\color{red}{\sf Part.3}$ 好了，让我们随机抽取一名幸运置换 $g$ 进行研究，看看有多少张图在经历 $g$ 后纹丝不动。 若隐若现的边太麻烦啦！不妨假设所有边都已存在，现在在我们面前的是一个 $n$ 个节点的完全图，然后我们需要给边们染色，染成存在或不存在两种颜色，从而得到 $X$ 中所有的图。  如何判断染成什么样子可以使得它成为置换 $g$ 中的不动点呢？ 注意到有些边是**等价**的，**等价的边一定要染成同一个颜色，要么同时存在，要么同时不存在**。 >例如一个三个顶点的三角形，如果置换 $g$ 的作用是将三个顶点顺时针轮换，那么这三条边是等价的（同属一个等价类），要么同时存在（形成一个完整的三角形），要么同时不存在（形成三个孤立的顶点）。不可能出现有两条边存在，一条边不存在的情况，否则经过一次旋转，缺口便到了另外两个点间，与原来的图就不同了。注意到此时三边同属 $1$ 个等价类，每个等价类要么染要么不染，因此在此置换 $g$ 下有 $2^1=2$ 个不动点。 >还是这个三角形，这回置换 $g$ 变为交换两个点，另一个点不动。那么两个动点间的边单独属于一个等价类，另外两条边属于另一等价类，一共有 $2$ 个等价类。每个等价类要么染要么不染，因此再此置换 $g$ 下有 $2^2=4$ 个不动点。 换句话说，对于置换 $g$ 如果存在 $k$ 个边的等价类，那么 $X$ 中就有 $2^k$ 个不动点。即： $$|X^g|=2^k$$ $$\,$$ $\color{red}{\sf Part.4}$ 好啦，接下来的问题就是求 $k$ ——置换 $g$ 下边的等价类个数。这部分是关键，而且有些绕，我们分两步走： #### 第一步，我们要将 $g$ 拆分为若干个不相交的循环置换。 这是什么意思呢？举个例子， $g$ 可以把点 $\{1,2,3,4,5,6\}$ 置换成 $\{2,3,1,5,4,6\}$ ，可以记作： $g= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 1 & 5 & 4 & 6 \end{pmatrix}$ 。注意到这个置换可以分解成几个不相交的部分，其中每个部分都是一个循环： $$ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 1 & 5 & 4 & 6 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix} $$ 现在将我们当前研究的置换 $g$ 拆成 $K$ 个循环，长度分别为 $b_1,b_2,\cdots,b_K$ 。 #### 第二步，将边按照端点分成两类 1._端点同时存在于同一循环内的边_。设循环长度为 $b$ ，则次循环共有 $\left \lfloor \frac{b}{2} \right \rfloor$ 个等价类。例如对于长度为 $6$ 的循环置换 $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 4 & 5 & 6 & 1 \end{pmatrix}$ ，我们把这 $6$ 个点排成正六边形：  （颜色相同的边同属于一个等价类） 不难发现两条边等价当且仅当它们长度相等，等价的边必须同时染/不染，否则会导致图案不具有旋转对称性，经过循环置换后也必定与原图不同。而正 b 边形中，共有 $\left \lfloor \frac{b}{2} \right \rfloor$ 种长度不同的线段，也就是对应 $\left \lfloor \frac{b}{2} \right \rfloor$ 个边的等价类。得证。 因此这一类边一共贡献了 $\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor$ 个等价类。 2._端点存在于不同循环内的边_ 。例如 $\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix}$ ，则连接 $3,4$ 的边不在同一循环内。这时，设两个循环的长度分别为 $b_1,b_2$ ，那么两个循环间共有 $b_1b_2$ 条这样的边。  （如上图，循环 $(1,2,3)$ 与 $(4,5)$ 间共有 $6$ 条边，但同属于 $\gcd(2,3)=1$ 个等价类） 每条边经过 ${\rm lcm}(b_1,b_2)$ 次循环后会回归原位，所以每个等价类大小为 ${\rm lcm}(b_1,b_2)$ 。也就是说，一共有 $\frac{b_1b_2}{{\rm lcm}(b_1,b_2)}=\gcd(b_1,b_2)$ 个等价类。别忘了，这只是 $g$ 内其中两个循环产生的贡献，要把每对循环的贡献累加起来，也就是： $\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)$ 个等价类。 至此两种情况已经分类讨论完毕，边的等价类个数就等于两种情况数量之和： $$k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)$$ $$|X/G|=\frac{1}{|G|}\sum_{g\in G}2^k$$ 是不是感觉离成功不远了呢（ $$\,$$ $\color{red}{\sf Part.5}$ 其实到了这里，我们已经找到计算文章开头数列的方法了。但是，别忘了 $|G|=n!$ ，枚举每一个置换 $g$ ，时间复杂度少说也得 $O(n!)$ 。我们是否以优化一下计算方法呢？ 注意到有许多置换会被重复计算，如下面两个置换： $$\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix}\qquad\begin{pmatrix} 1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 2 & 3\\ 3 & 2 \end{pmatrix} \circ \begin{pmatrix} 4 & 5 & 6\\ 6 & 4 & 5 \end{pmatrix}$$ 它们间没有本质上的区别，对应的 $k$ 值都相等（因为 $b$ 都是 $1,2,3$ ），本可以统一计算。 一般地，如果两个置换的循环长度排序后一一相等，那么两者对答案的贡献 $2^k$ 是相等的。因此，与其枚举每一种置换再拆分，不如枚举 $n$ 的拆分代表**一类置换**，再统一计算贡献。 例如 $n=5$ 时，它的拆分有 $(1,1,1,1,1),(1,1,1,2),(1,1,3),(1,2,2),(1,4),(2,3),(5)$ ，其中 $(1,2,2)$ 统一代表了形如 $$\begin{pmatrix} * \\ * \end{pmatrix} \circ \begin{pmatrix} * & *\\ * & * \end{pmatrix} \circ \begin{pmatrix} * & *\\ * & * \end{pmatrix}$$ 的置换。也就是循环长度 $b=\{1,2,2\}$ 的置换。 那么对于某个拆分，如何计算有多少对应的置换呢？ 首先 $1\sim n$ 随便放一共有 $n!$ 种方案，但长度为 $b$ 的循环会贡献 $b!$ 倍重复方案。所以单是分配每个元素在哪个循环中就有 $\frac{n!}{\prod(b_i!)}$ 种方案。 接着是循环的内部分配，也就是 $b_i$ 个元素的圆排列，有 $\prod(b_i-1)!$ 种方案。 但事实上，对于长度相等的循环它们之间可以彼此交换，本质上是一样的，因此还是会算重。设 $c$ 表示表某个长度的循环的个数，则会算重 $c!$ 倍。因此答案还需除以 $\prod(c_i!)$ 。 结合上述三项，可以得到，拆分 $b_i$ 所对应的置换个数为： $$\frac{n!}{\prod(b_i)\prod(c_i!)}$$ 用这个式子改进之前的 n! 枚举算法，可以得到： $$|X/G|=\frac{1}{|G|}\sum_b \frac{n!}{\prod(b_i)\prod(c_i!)} 2^k$$ $|G|=n!$ ，里外两项正好抵消，得到最终的形式： $$\,$$ $$\large{|X/G|=\sum_b \frac{2^k}{\prod(b_i)\prod(c_i!)}}$$ $$\large{k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)}$$ $$\,$$ **大功告成。** 最后再提一下时间复杂度。DFS枚举 $n$ 的拆分 $b$ ，再 $O(K^2)$ 求 $k$ 。增长速度是 [A000041](http://oeis.org/A000041)，[A296010](https://oeis.org/A296010) 的乘积。前者增速是 $O\left (\frac{e^{\sqrt{n}}}{n}\right )$，后者不知道。估计总复杂度大概在 $O(10^{\sqrt{x}})$ 左右。 $$\,$$ ```cpp #include<bits/stdc++.h> #define int long long using namespace std; int ans, n, p = 997, b[70], jc[70], jd[70]; int gcd(int a, int b){ return !b ? a : gcd(b, a % b); } int qpow(int A, int B){ int C = 1; while(B){ if(B & 1) C = C * A % p; A = A * A % p, B >>= 1; } return C; } void init(){ jc[0] = 1; for(int i = 1; i < 70; i++){ jc[i] = i * jc[i - 1] % p; } // 预处理阶乘 } void work(int len){ int u = 0, v = 1; for(int i = 1; i <= len; i++){ u += b[i] >> 1; for(int j = 1; j < i; j++){ u += gcd(b[i], b[j]); } // 计算边的等价类个数，u 即题解的 k } for(int i = 1; i <= len; i++){ v = v * b[i] % p; } for(int i = 1, j; i <= len;){ for(j = i; b[i] == b[j] && j <= len; j++); v = v * jc[j - i] % p; // 去除长度相等的循环带来的重复计算 i = j; } ans = (ans + qpow(v, p - 2) * qpow(2, u) % p) % p; } void dfs(int now, int last, int rem){ if(!rem){ // DFS 枚举 n 的所有拆分 work(now - 1); return; } for(int i = last; i <= rem; i++){ b[now] = i; dfs(now + 1, i, rem - i); } } signed main(){ cin >> n; init(); dfs(1, 1, n); cout << ans; return 0; } ``` $$\,$$ $\color{red}{\sf Part.6}$ 不妨思考形式更一般的问题： #### $n$ 个节点的完全无向图，用 $m$ 种颜色给每条边染色，可以染出几种互不同构的图？ 答案十分简单，只需要将上述式子中的 2 改为 m 即可： $$\,$$ $$\large{|X/G|=\sum_b \frac{\color{red}{m}^\color{black}k}{\prod(b_i)\prod(c_i!)}}$$ $$\large{k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)}$$ $$\,$$ 因为在原问题中，每条边有存在/不存在两种情况，这等价于用两种颜色给每条边染色，不动点数为 $2^k$ 。现在改为用 $m$ 种颜色染色，自然就是 $m^k$ 了。 ~~双倍经验：P4128~~