题解 P1429 【平面最近点对（加强版）】
syksykCCC
2019-06-23 12:40:12
**UPD：谢谢大家对之前题解的支持，这里我重新更换一下以前难看的图片，同时补补锅，回答一下疑点。**
**UPD2：根据新的题解规范修改了文章。另外大家喜欢的话不妨点点赞支持支持。**
**UPD3：应评论要求补充了时间复杂度分析。另外发现题解的图片中 $\rm P_9$ 和 $\rm P_{10}$ 全部标反了，但因为不影响算法理解，且原图源丢失，暂时请大家阅读时自行对换过来。**
----
首先感谢：
* @[plane](https://www.luogu.org/space/show?uid=277) 和他的[题解](https://www.luogu.org/blog/user277/solution-p1429)；
* @[frankchenfu](https://www.luogu.org/space/show?uid=23398) 和他的[题解](https://www.luogu.org/blog/frankchenfu/solution-p1429)。
下面我贴上 @[frankchenfu](https://www.luogu.org/space/show?uid=23398) 的代码，我将给出图示模拟，希望能帮助看不懂的同学理解
```cpp
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 1000001;
const int INF = 2 << 20;
int n, temp[maxn];
struct Point
{
double x, y;
} S[maxn];
bool cmp(const Point &a, const Point &b)
{
if(a.x == b.x) return a.y < b.y;
else return a.x < b.x;
}
bool cmps(const int &a, const int &b) { return S[a].y < S[b].y; }
double min(double a, double b) { return a < b ? a : b; }
double dist(int i, int j)
{
double x = (S[i].x - S[j].x) * (S[i].x - S[j].x);
double y = (S[i].y - S[j].y) * (S[i].y - S[j].y);
return sqrt(x + y);
}
double merge(int left, int right)
{
double d = INF;
if(left == right) return d;
if(left + 1 == right) return dist(left, right);
int mid = left + right >> 1;
double d1 = merge(left, mid);
double d2 = merge(mid + 1, right);
d = min(d1, d2);
int i, j, k = 0;
for(i = left; i <= right; i++)
if(fabs(S[mid].x - S[i].x) < d) // 这里不太一样
temp[k++] = i;
sort(temp, temp + k, cmps);
for(i = 0; i < k; i++)
for(j = i + 1; j < k && S[temp[j]].y - S[temp[i]].y < d; j++)
{
double d3 = dist(temp[i], temp[j]);
if(d > d3) d = d3;
}
return d;
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i++) scanf("%lf%lf", &S[i].x, &S[i].y);
sort(S, S + n, cmp);
return !printf("%.4lf\n", merge(0, n - 1));
}
```
一个个来解释。
比如说我们拿到了这样一组样例：
> $\textbf{InputData:}$
> ```plain
> 10
> 1 1
> 1 5
> 3 1
> 5 1
> 5 6
> 6 7
> 7 3
> 8 1
> 10 3
> 9 9
> ```
这组样例是排好序的，我们可以得到这样的图：
[](https://cdn.luogu.com.cn/upload/pic/61217.png)
下面我们要开始 $\mathrm{merge()}$了。（注意我的图从 $1$ 开始编号，略有不同）
$\mathrm{merge}(\textit{left},\textit{right})$ 是返回由编号 $\textit{left}\sim \textit{right}$ 的点构成的最近点对的距离，所以 $\mathrm{merge}(1, n)$ 即为答案，因为这是一个递归函数，我们假设它已经能返回一个区域中的最近点对了。
```cpp
// 预处理
double d = INF;
if(left == right) return d;
if(left + 1 == right) return dist(left, right);
```
然后算出 $mid$ 并进行递归。
[](https://cdn.luogu.com.cn/upload/pic/61219.png )
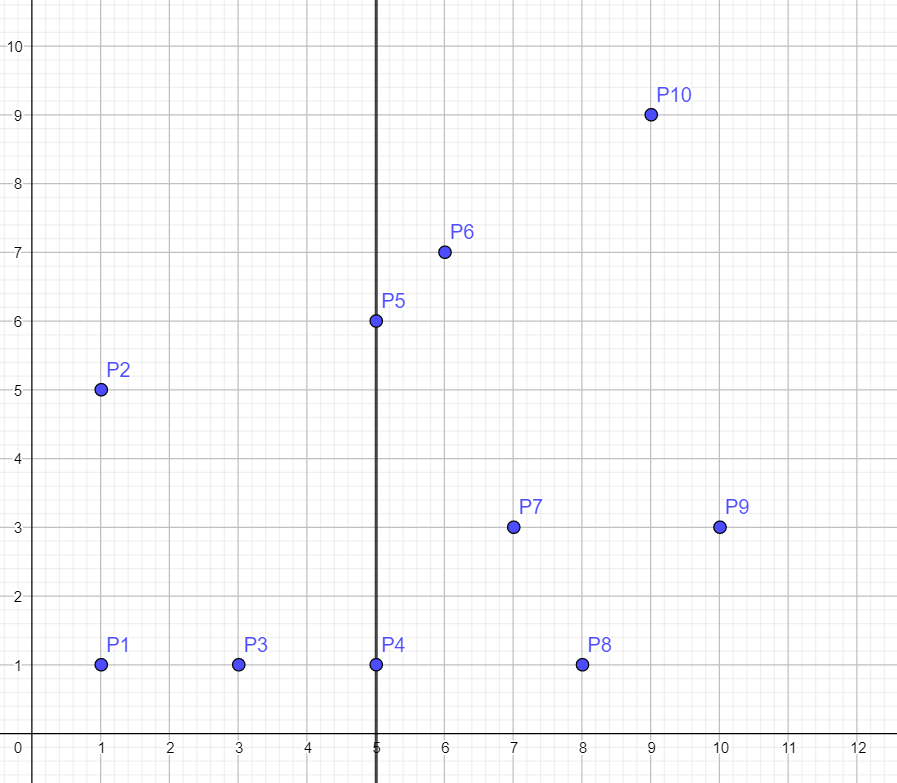
也就是求出 $[\text P_1\sim \text P_5]$ 和 $[\text P_6\sim \text P_{10}]$ 中的最近点对。
显然 $d_1=2$（$\text P_1$ 与 $\text P_3$ 之间），$d_2=\sqrt{5}$（$\text P_7$ 和 $\text P_8$ 之间）。
那么 $d = \min(d_1,d_2)=2$。
```cpp
// 递归
int mid = left + right >> 1;
double d1 = merge(left, mid);
double d2 = merge(mid + 1, right);
d = min(d1, d2);
```
[](https://cdn.luogu.com.cn/upload/pic/61221.png)
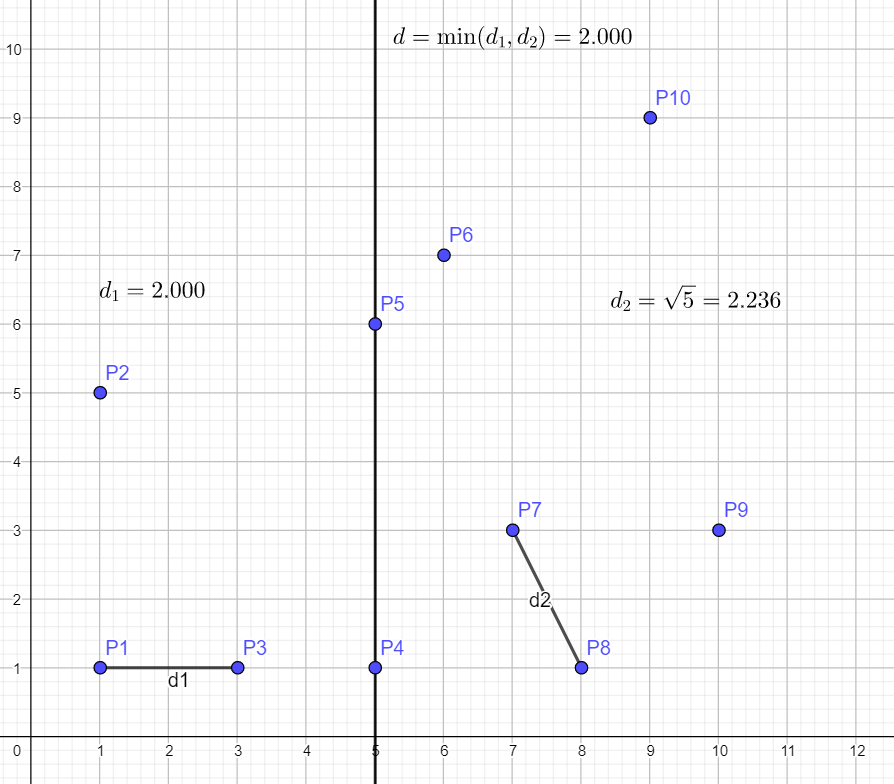
**前方高能**
接下来就是这个算法的核心，如何求出跨越蓝线的最近点对了。
首先锁定点集 $\text{Temp}$。
```cpp
// 求出temp[]并排序
for(i = left; i <= right; i++)
if(fabs(S[mid].x - S[i].x) < d)
temp[k++] = i;
sort(temp, temp + k, cmps);
```
[](https://cdn.luogu.com.cn/upload/pic/61218.png)
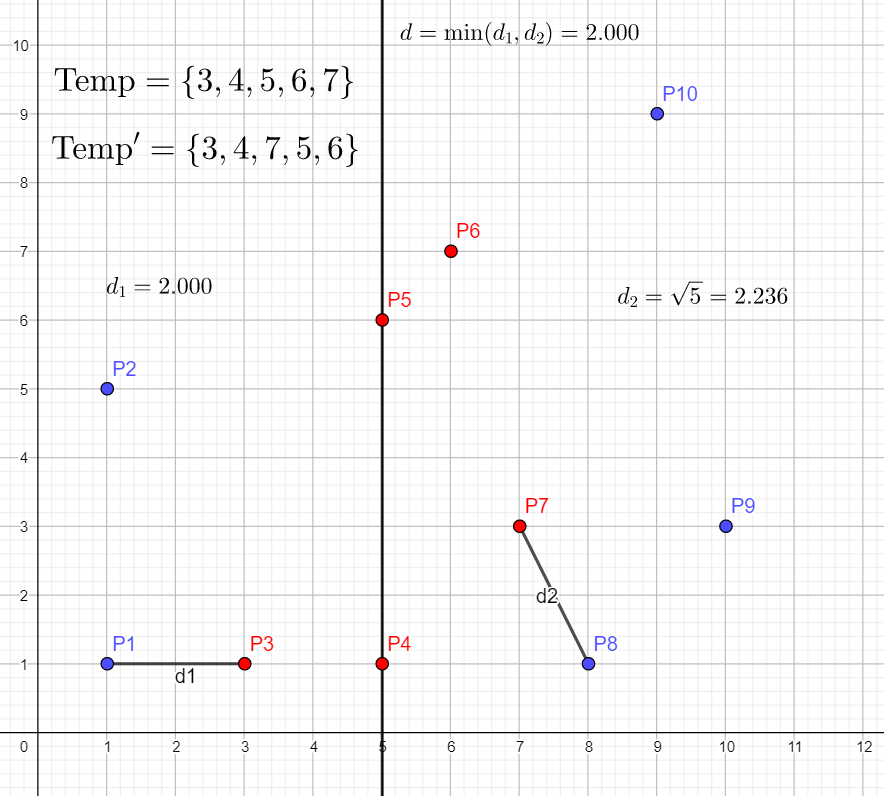
由程序可知 $\text{Temp}$ 包含了离直线距离不超过 $d$ 的所有点。
为啥其它点不用考虑呢？
**因为其它点离该线的距离都大于等于 ${d}$ 了，就更不用说到另一侧的点的距离了，必定不如直接返回 ${d}$ 来的优**。
而按照纵坐标排序是为了后面的方便。
```cpp
// 求出最近点对（TLE）
for(i = 0; i < k; i++)
for(j = i + 1; j < k; j++)
{
double d3 = dist(temp[i], temp[j]);
if(d > d3) d = d3;
}
```
相信这段代码大家都能看懂，但是很可惜，开 `-O2` 才能过，这是为什么呢？
不难发现源代码是这样的：
```cpp
// 求出最近点对
for(i = 0; i < k; i++)
for(j = i + 1; j < k && S[temp[j]].y - S[temp[i]].y < d; j++)
{
double d3 = dist(temp[i], temp[j]);
if(d > d3) d = d3;
}
```
好像多了一个 `S[temp[j]].y - S[temp[i]].y < d`，它有什么用呢？
和上面同理，**如果两者的纵坐标之差都大于等于 ${d}$ 了，那再计算就没有丝毫意义了，因为如果加上水平距离的话，必定不如直接返回 ${d}$ 来的优**。
例如 $\text P_3$ 号点，它只需和 $\text P_4$ 匹配就行了，因为它们的纵坐标之差为 $0$，有可能会带来更好的答案，而它和 $\text P_7$ 匹配就没有任何意义，因为即便它们的纵坐标之差等于 $d$，但就算 $\text P_7$ 在 $\text P_3$ 的正上方，距离也**不会小于** $d$。
值得注意的是，这里比如 $\text P_3$ 和 $\text P_4$ 会被重新计算，但对时间复杂度没有影响。
[](https://cdn.luogu.com.cn/upload/pic/61220.png)
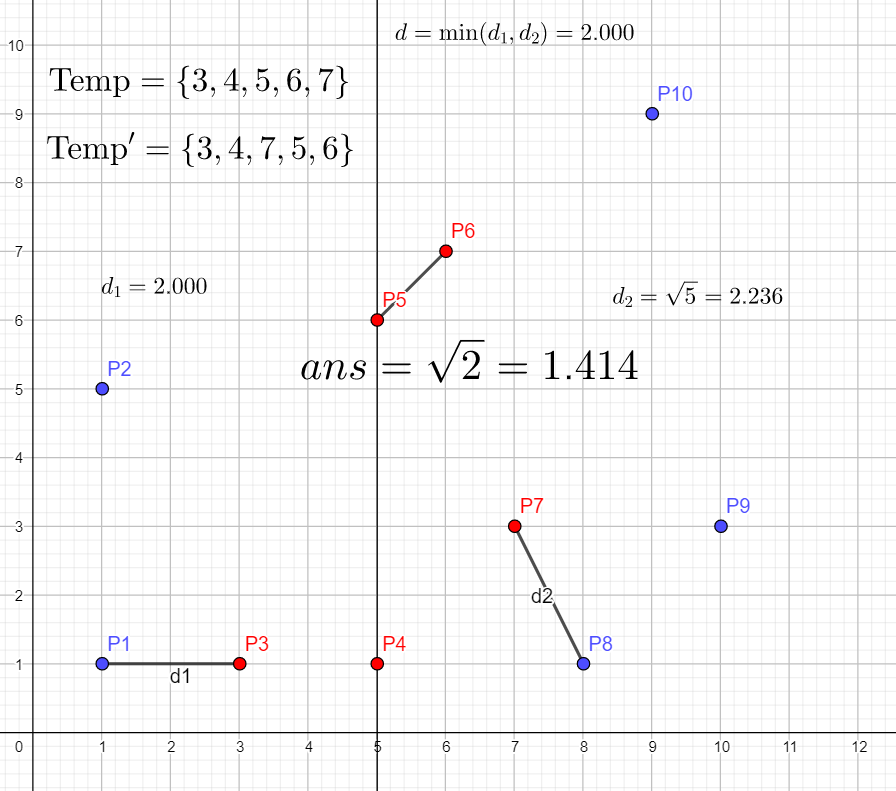
至此，我们求出了结果 $ans = \sqrt{2}$（$\text{P}_5$ 和 $\text P_6$ 之间）。
所以：
> $\textbf{OutputData:}$
> ```plain
> 1.4142
> ```
---
这个算法的时间复杂度又是怎么样的呢？（不想看分析的可以跳过）
考虑对于左边的一个点 $\text{P}_i$，**可能和它成为新的最近公共点对**的点 $\text{P}_j$ 有多少个。
```cpp
// 求出最近点对
for(i = 0; i < k; i++)
for(j = i + 1; j < k && S[temp[j]].y - S[temp[i]].y < d; j++)
{
double d3 = dist(temp[i], temp[j]);
if(d > d3) d = d3;
}
```
不难发现 $\text{P}_j$ 满足这些条件：
1. $\text{P}_j$ 与 $mid$ 线的距离小于 $d$。
2. $\text{P}_j$ 的纵坐标比 $P_i$ 大（因为如果 $\text{P}_j$ 的纵坐标比 $\text{P}_i$ 小，则这个状态会在之前考虑有哪些点可能与 $\text{P}_j$ 形成最近公共点对的时候考虑到，没必要重复考虑，虽然真的考虑的话也就只是 $2$ 倍常数）。
3. $\text{P}_j$ 和 $\text{P}_i$ 的纵坐标之差小于 $d$。
根据这三条，我们可以画出一个 $d \times 2d$ 的矩形，合法的 $\text{P}_j$ 一定是在这个矩形中的（不含边界）。
但是，我们又知道，如果两个点同在左侧，则距离 $\ge d$；如果两个点同在右侧，则距离 $\ge d$。
那么，无论是 $mid$ 左边的正方形还是右边的正方形，**每个里面都至多放 $3$ 个点（包括 $\text{P}_i$）**。
图中红色点即代表 $\text{P}_j$，展示了一种方案，其中每条虚线边的长度都 $\ge d$。
所以对于每个 $\text{P}_i$，检验至多其他 $5$ 个点即可，所以求最近点对的部分时间复杂度是 $O(n)$ 的！
（当然其实与 $\text{P}_i$ 同侧的 $\text{P}_j$ 是不可能对更新答案有用的，如果你愿意的话，检验至多 $3$ 个点即可）
于是整个代码的瓶颈就在 `sort` 上了，时间复杂度为 $T(n) = 2\cdot T(\frac n 2) + O(n \log n) = O(n \log^2 n)$，当然如果使用**归并排序替换 `sort`** 的话，就可以做到严格的 $O(n \log n)$！
---
最后，如果大家发现了问题，也欢迎大家指正哦！