题解 P3745 【[六省联考2017]期末考试】【三分+前缀和】
wjyyy
2018-12-11 21:18:25
稍微分析了一下三分的正确性,并用三分+前缀和的方式把$O(m\log m)$优化到了$O(m+\log m)$,表示瓶颈在于输入……
**[博客传送门](https://www.wjyyy.top/2818.html)**
## 题解:
首先分析一下本题的模型。可以想象成一个木桶效应,即“**短板**”的来源。

如图,即使最快改完卷子的课程用时为$0$,它也需要等待最慢改完卷子的课程。因此在改卷的人力定下来之后,**全部课程**改卷结束的时间是**唯一**的。既然不愉快度是由人力决定的,人力的改变也决定了完成的时间。
因此我们尝试确定一个结束时间,这样再贪心地分配人力,就可以求出以这个时间结束的最小不愉快度。

虚线此时是**要求改完卷子的时间**,那么在虚线右边的时间就需要通过调度老师或者增加老师来弥补。首先判断是否有$A\le B$,如果是,则虚线左边的空隙都可以拿来填补虚线右边的时间条,剩下的(若$A>B$,则剩下的就还是原来那么多)需要拿$B\times$天数来弥补。再根据学生的需要,把虚线左边的橙色线条到虚线的距离和都统计出来,乘上$C$,就是我们把结束时间定在虚线位置的不愉快度。
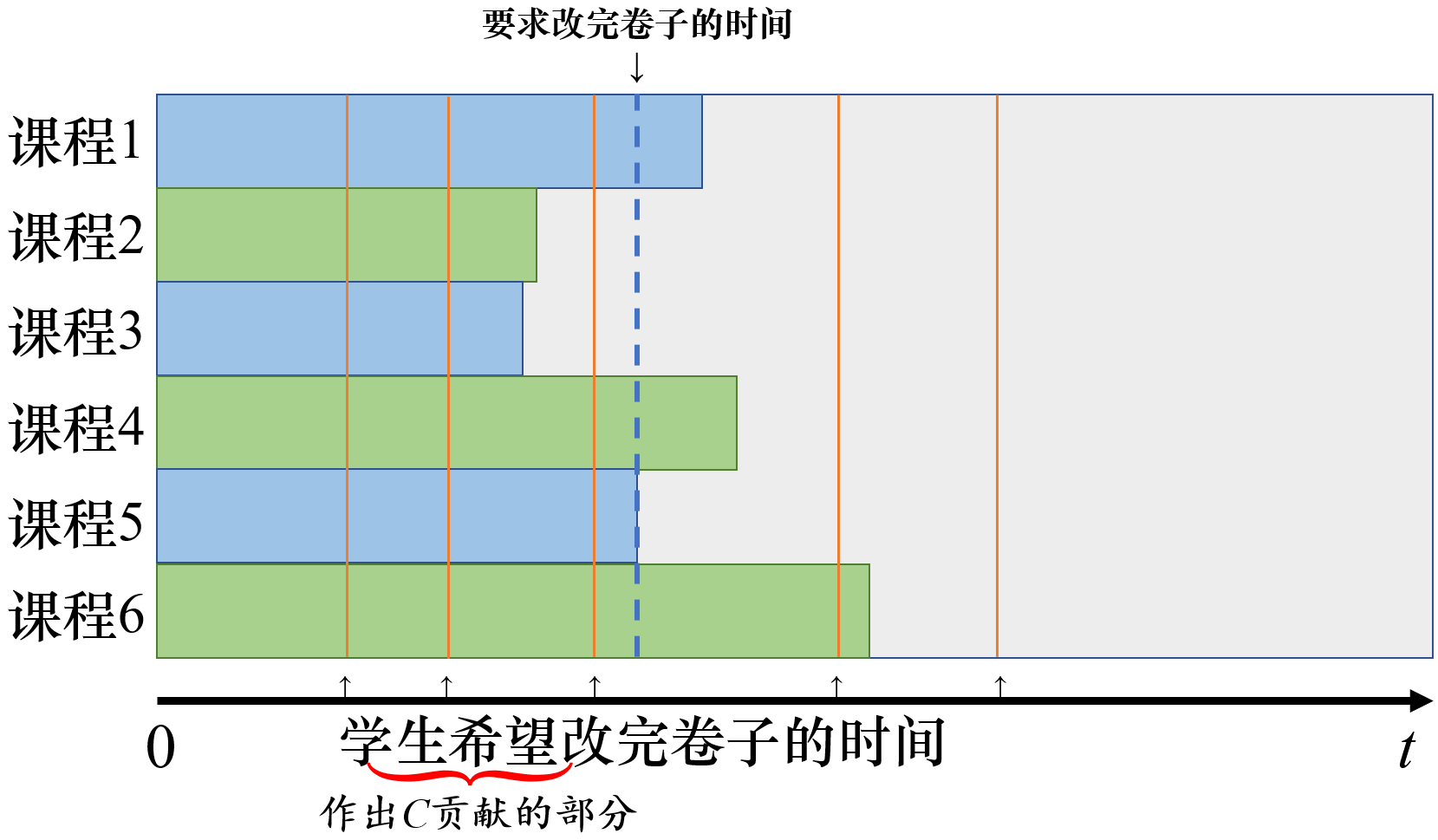
我们知道了这些,实际上就可以做这个题了,用两部分前缀和预处理一下,这个时间就可以从$max\{b_i\}$向前枚举了。不过害怕前缀和出问题的话,可以想想三分,此时要证不愉快度是单峰的。~~三分好像不比前缀和好写到哪去。~~
假设我们现在有最优解$x=t$,那么对于$x+a(a>0)$来说,一定有$ans_{x+a}>ans_x$。
理由是随着改卷结束时间(虚线)的增加,出现在虚线以左的橙线会在个数和距离上都不断增加,尽管由$A,B$产生的不愉快度会减小,但只是杯水车薪,况且这个减小的幅度也会越来越小,最后趋近于$0$。可能会有人担心这个不愉快度减小得比$C$部分增加得快,如果存在某解比最优解更优,它一定与最优解相邻,既然相邻就会一定被三分过程更新到。
对于$x-a$同理,$A,B$产生贡献增加的幅度会越来越大,而$C$产生的贡献幅度会越来越小。因此三分的正确性可以保证。
那么我们就有了$O(m\log b_i)$的优秀三分解法。再在三分内部使用前缀和,就可以做到$O(m+\log b_i)$了~~好神经啊~~。
注意要特判$C_i=10^{16}$的情况,这种情况就算全部补充老师也比让学生不满意优,因此直接贪心决策怎样调度老师。
## Code:
```cpp
#include<cstdio>
#include<cstring>
#define ll long long
#define N 100005
ll read()
{
ll x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x;
}
ll b[N],sum[N];//有多少人期望在第i天之前出成绩
ll sum1[N];//前面人的天数之和
ll Sum[N],Sum1[N];//这里维护的是出成绩时间前缀和
ll x,y,z,n,m;
ll f[N];//记忆化在第i天出成绩的代价(减小三分常数)
ll calc(int u)//要求在第u天出成绩
{
if(f[u]!=-1)
return f[u];
f[u]=0;
ll r=0,t=0;//r表示有多少余力 t表示还需要多少
r=Sum[u]*u-Sum1[u];
t=Sum1[N-1]-Sum1[u]-(Sum[N-1]-Sum[u])*u;
//↑O(1) ↓O(m)
/*for(int i=1;i<=m;++i)
if(b[i]>u)
t+=b[i]-u;
else
r+=u-b[i];
*/
//首先要填满 贪心看是调度便宜还是直接加便宜
if(x<y)
{
ll tmp=r<t?r:t;
f[u]+=tmp*x;
t-=tmp;
}
f[u]+=t*y;
f[u]+=(sum[u]*u-sum1[u])*z;
return f[u];
}
int main()
{
memset(f,-1,sizeof(f));
x=read();y=read();z=read();n=read();m=read();
int u,mn=N;
for(int i=1;i<=n;++i)
{
u=read();
++sum[u];
mn=mn<u?mn:u;
}
for(int i=1;i<N;++i)
{
sum1[i]=sum1[i-1]+sum[i]*i;
sum[i]+=sum[i-1];
}
for(int i=1;i<=m;++i)
{
b[i]=read();
++Sum[b[i]];
}
for(int i=1;i<N;++i)
{
Sum1[i]=Sum1[i-1]+Sum[i]*i;
Sum[i]+=Sum[i-1];
}
int l=0,r=N-1,mid;
if(z==10000000000000000)
r=mn;
while(l<r)
{
mid=(l+r)>>1;
ll y_=calc(mid),y__=calc(mid+1);
if(y_==y__)
{
printf("%lld\n",y_);
return 0;
}
else if(y_>y__)
l=mid+1;
else
r=mid;
}
printf("%lld\n",calc(l));
return 0;
}
```