SPFA算法的玄学方法
xhhkwy
·
·
算法·理论
按加号可以点赞!
最近想到了许多优化spfa的方法,这里想写个日报与大家探讨下
前置知识:spfa(不带任何优化)
由于使用较多STL,本文中所有代码的评测均开启O_2优化
对一些数组的定义:
$inq[i]$ : $i$是否存在队列当中
现在进入正题
------------
### 1.一些简单的优化(?)
**SLF(Small Label First)优化** 在使用queue作为spfa的辅助数据结构时,将队列替换为双端队列,每当插入元素$now$时,与队首进行比较,若$dis[q.front()] > dis[now]$,将$now$从队首插入,否则从队尾插入。
**LLL(Large Label Last)优化** 同样使用双端队列,维护目前队列中元素到起点的距离的平均值(即$∑^{tail}_{i =head}dis[que[i]]/q.size()$),设该数为$k$,若$dis[now] > k$,则从队尾插入,否则从队首插入。
由于这两种优化过于简单,不给出具体代码实现。
使用效果:只能让你的spfa跑的快一点,适用于常数大的同学。至于卡了spfa的题,仍旧没有什么用处。
$Q$:为什么这两种优化有用?
$A$:即使图经过了特殊构造(如网格图),但边权大部分随机的情况下。$SLF$能使得更可能更新出节点最优解的节点最先进行更新,减少无用迭代次数。而$LLL$优化我认为说实话用处不大,因为只要走上了一条权值特别大的边,这个优化就和没有一样了。
------------
### 2.一些升级过后的优化方式
**容错后的SLF** 定义容错值$val$,当满足$dis[now] > dis[q.front()] + val$时从队尾插入,否则从队首插入。
**mcfx优化** 定义区间$[l,r]$,当入队节点的入队次数属于这个区间的时候,从队首插入,否则从队尾插入。
**Swap-SLF** 若队列改变且$dis[q.front()] > dis[q.back()]$,交换队首队尾
代码实现以及评测
容错SLF+MCFX :https://www.luogu.org/record/show?rid=14511935
swap-SLF :https://www.luogu.org/recordnew/show/14512493
(这几个优化已经能过数据不刁钻的卡spfa的题,至于lg的模板...fstqwq就是看着这几个优化来卡的...)
$Q$:为什么这几种优化有用?
$A$:具体我也没有在网上找到,我说说自己理解的吧。容错SLF可以让你的程序不陷入局部最优解,与模拟退火类似;而mcfx优化是这样的,如过某个节点出发的大多数边都只能更新一个次解(说白了就是这个点如果是出题人用来故意让你经过多次的节点,并且每次更新会导致一次特别长的迭代,类似菊花图的根),那么它在队列中的优先级就会降低,就像你知道出题人用这个点来卡你,你竟然还把它最先拿来最先更新,肯定是不够好的;至于swap-SLF....我也没有搞懂为什么这个优化能比普通的SLF快辣么多(ComeIntoPower说这可以让队列更接近优队)...
------------
### 3.一些玄学的优化
**边序随机** 将读入给你的边随机打乱后进行spfa
**队列随机** 每个节点入队时,以1 / 2的概率从队首入队,1 / 2的概率从队尾入队。
**队列随机优化版** 每$C$次入队后,将队列元素随机打乱。
使用方法:一般配合上面的优化,当然如果你使用了队列随机...那么你只能靠rp啦。
边序随机代码实现:
```cpp
//如果你和我一样是用vector + pair存图的话,那么只需要加上这一行语句
for(int i = 1 ; i <= n ; ++i) random_shuffle(G[i].begin() , G[i].end());
//以及开头加上srand(time(NULL));
```
队列随机优化版+边序随机代码实现:
https://www.luogu.org/record/show?rid=14090021
------------
### 4.更改使用的数据结构
priorty_queue || zkw-segment-tree
当正权边上的时候,这两个数据结构优化的spfa与dijkstra相同...
(即使您的代码允许节点多次入队,但是也没什么用,因为一个节点最多进入一次队列)
而负权边的时候,这个算法又被称为允许多次入队的dijkstra,但是很危险,有可能被卡成指数级!
stack
dfs实现的spfa,被提出于姜碧野的论文,事实上,它用来判断负环可能十分快速(没必要进行多余的$N$次迭代)。但是如果是求最短路,一般不如队列版本spfa。为什么会这样呢?因为spfa_dfs一个次解就是一个$O(N)$的迭代,一种图可以轻而易举的卡爆它。
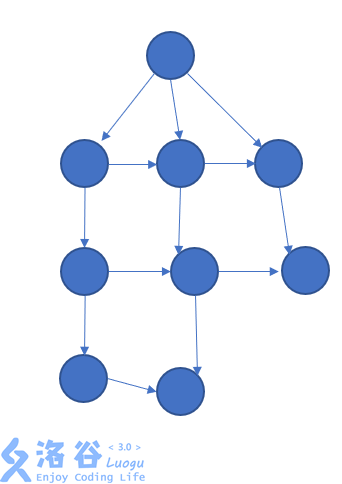
(ppt是真tm好用)
所以我们采用IDDFS逐渐放宽深度的方式,这样子spfa_dfs也能赶上spfa_bfs
------------
参考文献:
[1] : fstqwq的知乎回答
https://www.zhihu.com/question/292283275/answer/484871888
[2] : 姜碧野 《迭代求解的利器--spfa算法的优化及其应用》
https://wenku.baidu.com/view/f22d0d36ee06eff9aef807e9.html