题解 CF594E 【Cutting the Line】

> [CF594E Cutting the Line](https://codeforces.com/contest/594/problem/E) > > 做法来自 [wucstdio 神仙的题解](https://www.luogu.com.cn/blog/wucstdio/solution-cf594e)，表述经过了一定的修改，也许会好懂一些？ ## 题意 - 给定一个字符串 $s$ 和一个正整数 $k$。 - 你可以将 $s$ 分成至多 $k$ 段，并将每一段翻转或者不翻转。 - 求最终能够得到的字典序最小的 $s$。 - $|s| \le 5 \times 10^6$。 ## 题解 令 $n = |s|$。 ### $k = 1$ 这种情况需要特判，比较 $s$ 和 $s^r$ 哪个小即可。 ### $k = n$ 当 $k = n$ 时，没有分割数量的限制。 对于某一段，如果不翻转它，可以看成**分割成单个字符后翻转**。因此此时一定存在一个最优解，满足分割后的每一段都翻转。 将问题转化一下，等价于每次从 $s^r$ 中截取一个后缀拼接在当前字符串之后。 那么显然我们应该贪心地截取最小后缀，Lyndon 分解即可。 ### $k < n$ 当 $k$ 变小时，我们需要尽量节约一点分割次数。 因此对于相邻两次分割，我们给出两个原则： 1. 如果**截取的字符串相同**，可以合并为一次。 2. 如果**截取的字符串都是回文串**，可以合并为一次，然后对这一次进行翻转。 ### $k \ge 3$ 对 $s^r$ 做 Lyndon 分解，设其最小后缀为 $t$，出现在结尾次数为 $c$。 根据刚才节约分割次数的原则 1，我们显然应该考虑截取 $c \times t$。 但是因为原则 2，这样还并不是最优的。 由于截取的字符是最小后缀，因此如果它们为回文串，其长度必然为 $1$。 因此策略如下： - 如果 $|t| \ne 1$，则截取 $c \times t$，然后让 $k$ 减 $1$。 - 如果 $|t| = 1$，且前一个 Lyndon 串的长度不为 $1$，则截取 $t$，然后让 $k$ 减 $1$。 - 如果 $|t| = 1$，且前一个 Lyndon 串的长度也为 $1$，则截取 $t$，但不消耗 $k$。 ### $k = 2$ 一种做法是枚举分割点，使用 SAM 实现 $\mathcal O(1)$ 查询任意两个子串的 LCP，总时间复杂度为 $\mathcal O(n)$。 然而，这个做法过于暴力，实现不够优美，最重要的是，我也不会 SAM。 现在的问题是，有一个字符串 $s$（原串的反串），你要截取一个后缀 $t_1$，剩下的部分为 $t_2$，对于 $t_1,t_2$，你都可以选择翻转或不翻转，要使 $t_1 + t_2$ 最小。 分类讨论一下： #### $t_1$ 翻转，$t_2$ 翻转 就是 $s^r$。 #### $t_1$ 不翻转，$t_2$ 不翻转 相当于要求 $s$ 的**最小表示**，有多种方法，Lyndon 分解也可以求。 #### $t_1$ 翻转，$t_2$ 不翻转 从后往前枚举分割点 $i$，假设当前最优分割点为 $j$，相当于比较 $(s[i:j-1])^r + s[:i-1]$ 和 $s[:j-1]$ 的大小。 可以转化为两次询问： - $(s[i:j-1])^r$ 和 $s$ 的 LCP 长度 - $s$ 和 $s[j-i+1:j-1]$ 的 LCP 长度 由于都是关于 $s$ 的询问，因此考虑使用 exkmp 求。 #### $t_1$ 不翻转，$t_2$ 翻转 设 $s$ 的 Lyndon 分解为 $a_1^{c_1} + a_2^{c_2} + \cdots + a_m^{c_m}$，其中 $a_1 > a_2 > \cdots > a_m$。 设 $b_i = a_i^{c_i}$，则 $s$ 的 Lyndon 分解也可以写成 $b_1 + b_2 + \cdots + b_m$。 设 $B_i = b_i + b_{i+1} + \cdots + b_m$。 显然，最优分割点一定在 Lyndon 分解的分割点上。 进一步地可以证明，$t_1$ 一定是某个 $B_i$，因为如果不是，意味着分割点前后都是 $a_i$，那么分割点移到 $b_i$ 头尾的分割点上一定有一种更优。 由于 $B_i > B_{i+1}$ 可知，除非 $B_{i+1}$ 是 $B_i$ 的前缀，否则 $t_1 = B_{i+1}$ 比 $t_1 = B_i$ 优。 因此我们取最后一个满足 $B_p$ 不是 $B_{p-1}$ 的前缀的 $p$，则最优分割点一定 $\ge p$。 对于 $i \ge p$，如果 $t_1 = B_i$ 比 $t_1 = B_{i-1}$ 更优，由于 $B_i$ 是 $B_{i-1}$ 的前缀，而 $B_{i-1}$ 又是 $B_{i-2}$ 的前缀，因此 $t_1 = B_i$ 比 $t_1 = B_{i-2}$ 更优（如果这句话无法理解，可以利用下图辅助理解，图来自 wucstdio）。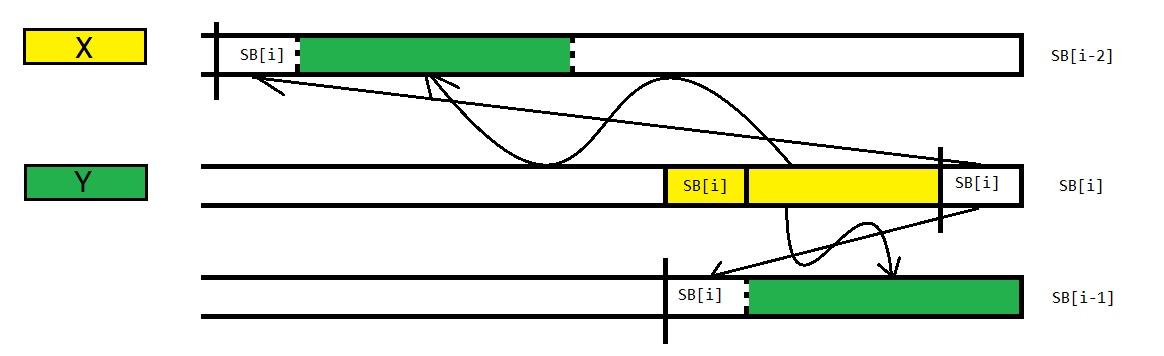  换句话说，我们只需要找到最大的 $q(>p)$，满足 $t_1 = B_q$ 比 $t_1 = B_{q-1}$ 更优，则 $t_1 = B_q$ 就是最优解。如果不存在 $q$，则 $t_1 = B_p$ 就是最优解。 暴力比较一次 $t_1 = B_q$ 和 $t_1 = B_{q-1}$ 是 $\mathcal O(|B_{q-1}|)$ 的，因此这么做的时间复杂度为 $\mathcal O(\sum_{i=p}^{m-1}|B_i|)$ 的，看起来很大。 但是，由于对于 $i \ge p$，$B_{i+1}$ 是 $B_i$ 的前缀，又根据 Lyndon 分解的性质，可以得到 $|b_i| > |B_{i+1}|$，因此 $|B_{i+1}| < \frac{|B_i|}2$。 于是 $\mathcal O(\sum_{i=p}^{m-1}|B_i|) = \mathcal O(|B_p|)$，我们得到了一个优美的线性做法。 ### 总结 回顾一下整个 $\mathcal O(n)$ 算法流程： 1. 特判 $k = 1$ 的情况。 2. 将 $s$ 翻转，Lyndon 分解。 3. 当 $k \ge 3$ 时，设最后一个 Lyndon 串为 $t$，出现次数为 $c$，不断重复以下策略，直到 $k = 2$： - 如果 $|t| \ne 1$，则截取 $c \times t$，然后让 $k$ 减 $1$。 - 如果 $|t| = 1$，且前一个 Lyndon 串的长度不为 $1$，则截取 $t$，然后让 $k$ 减 $1$。 - 如果 $|t| = 1$，且前一个 Lyndon 串的长度也为 $1$，则截取 $t$，但不消耗 $k$。 4. 当 $k = 2$ 时，设截取的后缀为 $t_1$，剩下的部分为 $t_2$，分类讨论： - $t_1$ 翻转，$t_2$ 翻转：$s^r$。 - $t_1$ 不翻转，$t_2$ 不翻转：$s$ 的最小表示。 - $t_1$ 翻转，$t_2$ 不翻转：枚举分割点，exkmp 实现。 - $t_1$ 不翻转，$t_2$ 翻转：找到最后一个满足 $B_p$ 不是 $B_{p-1}$ 的前缀的 $p$，再找到最大的 $q(>p)$，满足 $t_1 = B_q$ 比 $t_1 = B_{q-1}$ 更优，此时 $t_1 = B_q$ 就是最优解，如果不存在 $q$，则 $t_1 = B_p$ 就是最优解。 ## 代码 ```cpp #define pc putchar const int N = 5e6 + 7; int n, k, r[N], l[N], t, z[N], p[N]; char s[N], ans[N], ss[N*2]; inline void Lyndon(char *s, int n, int *r, int *l, int &t) { t = 0; int i = 1; while (i <= n) { int j = i, k = i + 1; while (k <= n && s[j] <= s[k]) j = s[j] == s[k++] ? j + 1 : i; while (i <= j) i += k - j; r[++t] = i - 1, l[t] = k - j; } } inline void k1() { for (int i = 1; i <= n; i++) { if (s[n+1-i] == s[i]) continue; if (s[n+1-i] < s[i]) reverse(s + 1, s + n + 1); break; } for (int i = 1; i <= n; i++) pc(s[i]); } inline void k3() { for (int i = r[t-1] + 1; i <= r[t]; i++) pc(s[i]); k -= l[t] != 1 || l[t-1] != 1, --t; } inline void upd(char *s) { for (int i = 1; i <= n; i++) { if (s[i] > ans[i]) return; if (s[i] < ans[i]) break; } for (int i = 1; i <= n; i++) ans[i] = s[i]; } inline void upd1() { reverse(s + 1, s + n + 1); upd(s); reverse(s + 1, s + n + 1); } inline void upd2() { for (int i = 1; i <= n; i++) ss[i] = ss[i+n] = s[i]; int i = 1, o; while (i <= n) { o = i; int j = i, k = i + 1; while (k <= n * 2 && ss[j] <= ss[k]) j = ss[j] == ss[k++] ? j + 1 : i; while (i <= j) i += k - j; } upd(ss + o - 1); } inline void Z(char *s, int n, int *z) { for (int i = 1; i <= n; i++) z[i] = 0; z[1] = n; for (int i = 2, l = 0, r = 0; i <= n; i++) { if (i <= r) z[i] = min(z[i-l+1], r - i + 1); while (i + z[i] <= n && s[i+z[i]] == s[z[i]+1]) ++z[i]; if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1; } } inline void exkmp(char *s, int n, char *t, int m, int *z, int *p) { Z(t, m, z); for (int i = 1; i <= n; i++) p[i] = 0; for (int i = 1, l = 0, r = 0; i <= n; i++) { if (i <= r) p[i] = min(z[i-l+1], r - i + 1); while (i + p[i] <= n && s[i+p[i]] == t[p[i]+1]) ++p[i]; if (i + p[i] - 1 > r) l = i, r = i + p[i] - 1; } } inline void upd3() { for (int i = 1; i <= n; i++) ss[i] = s[i]; reverse(ss + 1, ss + n + 1); exkmp(ss, n, s, n, z, p); reverse(p + 1, p + n + 1); int j = n; for (int i = n - 1; i; i--) if (p[j-1] < j - i) { if (s[j-1-p[j-1]] < s[p[j-1]+1]) j = i; } else if (z[j-i+1] < i - 1) { if (s[z[j-i+1]+1] < s[j-i+1+z[j-i+1]]) j = i; } reverse(s + 1, s + j); reverse(s + 1, s + n + 1); upd(s); reverse(s + 1, s + n + 1); reverse(s + 1, s + j); } inline void upd4() { int p = t + 1; while (--p > 1) { bool ok = 1; for (int i = r[p-1] + 1, j = r[p-2] + 1; ok && i <= r[p]; i++, j++) if (s[i] != s[j]) ok = 0; if (!ok) break; } int q = p; while (++q <= t) for (int i = r[q-1], j = r[q-2] + 1 + n - i; i > r[q-2]; i--, j++) { if (s[i] == s[j]) continue; if (s[i] < s[j]) p = q; break; } reverse(s + r[p-1] + 1, s + n + 1); reverse(s + 1, s + n + 1); upd(s); reverse(s + 1, s + n + 1); reverse(s + r[p-1] + 1, s + n + 1); } inline void k2() { for (int i = 1; i <= n; i++) ans[i] = s[i]; upd1(), upd2(), upd3(), upd4(); } int main() { rds(s, n), rd(k); if (k == 1) return k1(), 0; reverse(s + 1, s + n + 1); Lyndon(s, n, r, l, t); while (k >= 3 && t) k3(); if ((n = r[t])) k2(); for (int i = 1; i <= n; i++) pc(ans[i]); return 0; } ```