题解 P8820【[CSP-S 2022] 数据传输】
yukimianyan
·
·
题解
problem
一棵 n 个点的树。如果两个点在树上的距离不超过 k,我们称这两个点可以互相传送信息。现在 q 次给定 s,t,选出 h=\{h_1=s,h_2,h_3,\cdots,h_{c-1},h_c=t\} 这 c 个点,满足相邻两个点可以互相传送信息,请最小化 \sum_{i\in h}v_i。
前置知识
\{\max,+\} 矩阵乘法 / 动态 DP。对于矩阵 a,b,c,这是我们所熟知的矩阵乘法 c=a\times b:
c=a\times b\Rightarrow c_{i,j}=\sum_{k}a_{i,k}b_{k,j}.
现在我们定义矩阵 * 法:
c=a*b\Rightarrow c_{i,j}=\min_{k}\{a_{i,k}+b_{k,j}\}.
为了更好地理解矩阵 * 法,您可以认为,c_{i,j} 的值是 a 的第 i 行顺时针旋转 90^\circ 后与 b 的第 j 列依次相加取最小值的结果。如果某一个值是 \infty 代表强制不选,如果是 0 代表继承。
我们可以证明,矩阵 * 法没有交换律,但有结合律。
solution when k\leq 2
$$\begin{bmatrix}f_{i-1}\end{bmatrix}*\begin{bmatrix}v_{h_i}\end{bmatrix}=\begin{bmatrix}f_i\end{bmatrix}.$$
$k=2$ 时一定会在链上走,如果走下去了回不去,答案更劣。
$$\begin{bmatrix}f_{i-1},f_{i-2}\end{bmatrix}
*\begin{bmatrix}
v_{h_i},&0\\
v_{h_i},&\infty\\
\end{bmatrix}
=\begin{bmatrix}f_{i},f_{i-1}\end{bmatrix}.$$
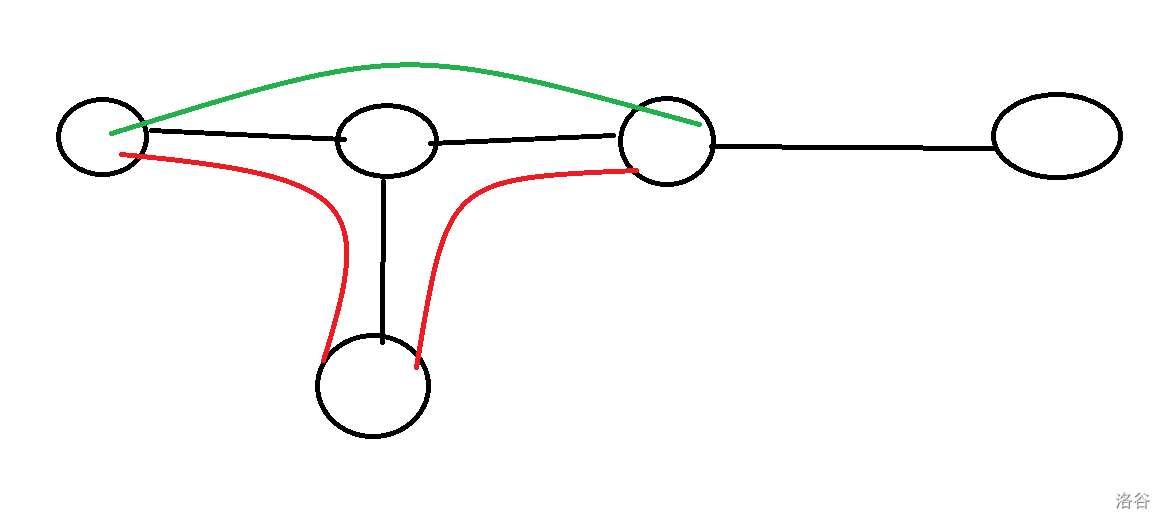
(走下去再返回(即红边)不如不走(即绿边))
## solution when $k=3
$$\begin{cases}
b_i&=\min_{\text{j是i的儿子或父亲}} v_j.\\
f_{i,0}&=\min\{f_{i-3,0},f_{i-2,0},f_{i-2,1},f_{i-1,0},f_{i-1,1}\}+v_{h_i}.\\
f_{i,1}&=\min\{f_{i-2,0},f_{i-1,0},f_{i-1,1}\}+b_{h_i}.\\
\end{cases}$$
考虑优化:我们不太关心这些点在链上还是不在链上。令 $f_{i,j}$ 表示现在在离第 $i$ 个点距离为 $j$ 的点上。重定义 $b_i=\min_{\text{j是i的儿子}} v_j$。
$$\begin{bmatrix}f_{i-1,0},f_{i-1,1},f_{i-1,2}\end{bmatrix}
*\begin{bmatrix}
v_{h_i},&0,&\infty\\
v_{h_i},&b_{h_i},&0\\
v_{h_i},&\infty,&\infty\\
\end{bmatrix}
=\begin{bmatrix}f_{i,0},f_{i,1},f_{i,2}\end{bmatrix}
$$
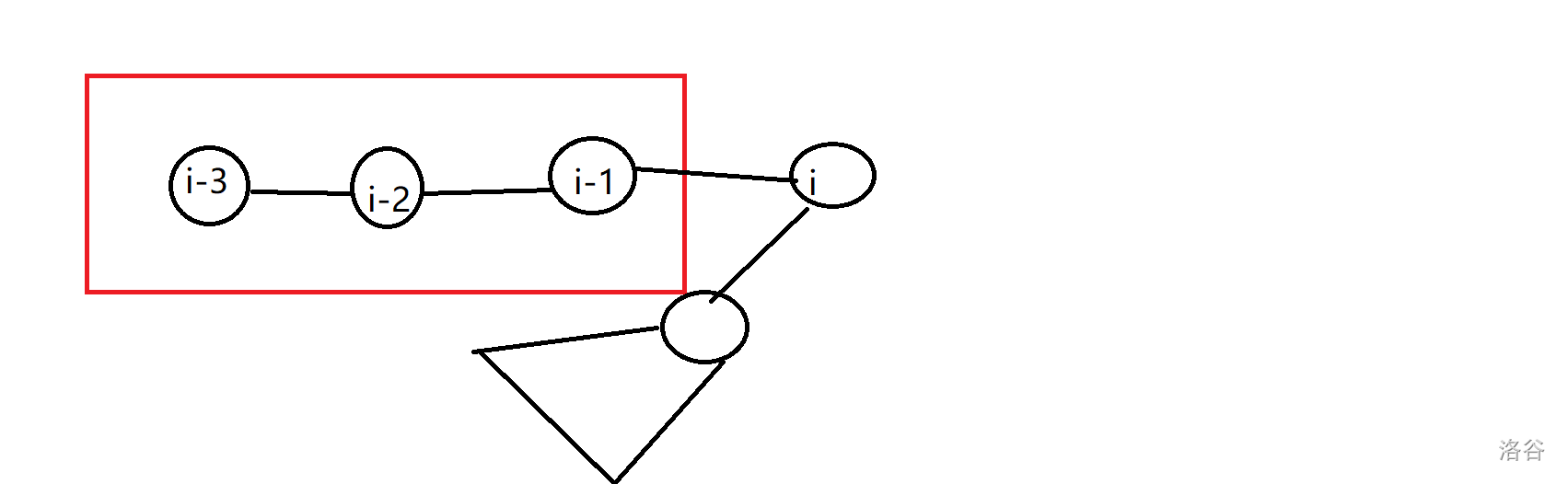
(这里转移不用关心走到 $i-1$ 的情况,已经在 $f_{i-1,0}$ 那里算过了,不用管)
(这里 $b_i$ 仅限儿子,在 LCA 处要稍微动一下,加上父亲的贡献)
(为了不分讨,可以强行认为 $f_0=\begin{bmatrix}\infty,\infty,0\end{bmatrix}$,尽管它并没有实际意义)
于是你会了暴力。
## solution 的优化
考虑把这玩意多组询问。
观察到每一个转移矩阵只和 $h_i,v_{h_i},b_{h_i}$ 有关,而后两个可以预处理,那么转移矩阵可以预处理。
模仿倍增 LCA,我们也整一个 $dw_{i,j},up_{i,j}$,分别表示以 $i$ 为最后一个点,从上往下 / 从下往上数 $2^j$ 个父亲的矩阵 $*$ 和。转移可以从 $2^{j-1}$ 那里拼起来,$O(nk^3\log n)$;询问可以把路径拆成 $s\to lca(s,t),lca(s,t),lca(s,t)\to t$ 三段,分别 $O(k^3\log n)$ 的求出矩阵 $*$ 和,求出答案即可。
注意到在 $lca$ 处可能走到它的父亲上,我们直接改它的转移矩阵中的 $b_i$ 即可。
总的复杂度为 $O((n+q)k^3\log n)$。
## code
```cpp
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef long long LL;
template<int N,int M,class T=LL> struct matrix{
T a[N][M];
matrix(T flag=1e18){memset(a,0x3f,sizeof a);for(int i=0;i<N&&i<M;i++) a[i][i]=flag;}
T* operator[](int i){return a[i];}
};
template<int N,int M,int R,class T=LL> matrix<N,R,T> operator*(matrix<N,M,T> a,matrix<M,R,T> b){
matrix<N,R,T> c=1e18;
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
for(int k=0;k<R;k++){
c[i][k]=min(c[i][k],a[i][j]+b[j][k]);
}
}
}
return c;
};
template<int N,int M,class T=int> struct graph{
int head[N+10],nxt[M*2+10],cnt;
struct edge{
int u,v; T w;
edge(int u=0,int v=0,T w=0):u(u),v(v),w(w){}
} e[M*2+10];
graph(){memset(head,cnt=0,sizeof head);}
edge& operator[](int i){return e[i];}
void add(int u,int v,T w=0){e[++cnt]=edge(u,v,w),nxt[cnt]=head[u],head[u]=cnt;}
void link(int u,int v,T w=0){add(u,v,w),add(v,u,w);}
};
LL a[200010],b[200010];
int n,m,sshwy,fa[19][200010],dep[200010];
graph<200010,200010> g;
matrix<3,3> dw[19][200010],up[19][200010];
matrix<1,3> f0;
matrix<3,3> gettrans(int i,LL del=1e18){
matrix<3,3> c=1e18;
switch(sshwy){
case 1: c[0][0]=a[i]; break;
case 2: c[0][1]=0,c[0][0]=c[1][0]=a[i]; break;
case 3: c[0][0]=c[1][0]=c[2][0]=a[i],c[0][1]=c[1][2]=0,c[1][1]=min(b[i],del); break;
}
return c;
}
void dfs(int u,int f=0){
dep[u]=dep[fa[0][u]=f]+1,b[u]=1e18;
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v; if(v==f) continue;
dfs(v,u),b[u]=min(b[u],a[v]);
}
dw[0][u]=up[0][u]=gettrans(u);
}
int lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v); int d=dep[u]-dep[v];
for(int j=18;j>=0;j--) if(d>>j&1) u=fa[j][u];
if(u==v) return u;
for(int j=18;j>=0;j--) if(fa[j][u]!=fa[j][v]) u=fa[j][u],v=fa[j][v];
return fa[0][u];
}
matrix<3,3> query_dw(int u,int k){
matrix<3,3> res=0;
for(int j=18;j>=0;j--) if(k>>j&1) res=dw[j][u]*res,u=fa[j][u];
return res;
}
matrix<3,3> query_up(int u,int k){
matrix<3,3> res=0;
for(int j=18;j>=0;j--) if(k>>j&1) res=res*up[j][u],u=fa[j][u];
return res;
}
LL query(int u,int v){
int k=lca(u,v);
matrix<1,3> res=f0*query_up(u,dep[u]-dep[k])*gettrans(k,a[fa[0][k]])*query_dw(v,dep[v]-dep[k])
return min({res[0][0]-a[v],res[0][1],res[0][2]})+a[v];
}
int main(){
scanf("%d%d%d",&n,&m,&sshwy);
f0[0][sshwy-1]=0,a[0]=1e18;
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),g.link(u,v);
dfs(1);
for(int j=1;j<=18;j++){
for(int i=1;i<=n;i++) fa[j][i]=fa[j-1][fa[j-1][i]];
for(int i=1;i<=n;i++) dw[j][i]=dw[j-1][fa[j-1][i]]*dw[j-1][i];
for(int i=1;i<=n;i++) up[j][i]=up[j-1][i]*up[j-1][fa[j-1][i]];
}
for(int u,v;m--;) scanf("%d%d",&u,&v),printf("%lld\n",query(u,v));
return 0;
}
```