浅谈牛顿迭代法
隔壁的张栩嘉
·
·
算法·理论
写在前面
由于作者是一个初一蒟蒻,有一些地方可能存在问题,请多指教。喷轻点
感谢@biiwx123 大佬指出\text{Part\ 2}求e^x标程的错误
感谢@Thinking 大佬指出\text{Part\ 3} f'的错误
你以为我会先讲牛迭吗?
不可能!
先说说牛顿迭代法他爸的创始人——Newton
艾萨克·牛顿(1643年1月4日—1727年3月31日)爵士,英国皇家学会会长,英国著名的物理学家,百科全书式的“全才”,著有《自然哲学的数学原理》、《光学》。
他在1687年发表的论文《自然定律》里,对万有引力和三大运动定律进行了描述。这些描述奠定了此后三个世纪里物理世界的科学观点,并成为了现代工程学的基础。
他通过论证开普勒行星运动定律与他的引力理论间的一致性,展示了地面物体与天体的运动都遵循着相同的自然定律;为太阳中心说提供了强有力的理论支持,并推动了科学革命。
在力学上,牛顿阐明了动量和角动量守恒的原理,提出牛顿运动定律。
在光学上,他发明了反射望远镜,并基于对三棱镜将白光发散成可见光谱的观察,发展出了颜色理论。他还系统地表述了冷却定律,并研究了音速。
在数学上,牛顿与戈特弗里德·威廉·莱布尼茨分享了发展出微积分学的荣誉。他也证明了广义二项式定理,提出了“牛顿法”以趋近函数的零点,并为幂级数的研究做出了贡献。
在经济学上,牛顿提出金本位制度。
——摘自百度百科
注意这句话:
他也证明了广义二项式定理,提出了“牛顿法”以趋近函数的零点,并为幂级数的研究做出了贡献。
这里的“牛顿法”就是今天要讲的牛顿迭代法啦!
牛顿迭代法的故事
很久很久以前,次数高于四次方程不存在求根公式……
关于这个问题,大佬伽罗瓦用群论证明了。
因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。前面几项来寻找方程的根。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。
一位大佬——牛顿横空出世,他想到一个神奇的东西 —— 泰勒公式。
f(x)=\lim_{n\to \infty}\sum_{i=0}^{n}\frac{f^{(n)}(x_0)}{i!}(x-x_0)^i+R_n(x)
可是,$n\to\infty$,难道我们要$\Theta(\infty)$?~~那牛顿迭代法有什么用?~~
$$\large\color{red}\text{在\ OI\ 中,一般\ }n=10\text{\ 够了}$$
但也不排除一些很坑的函数,这种另当别论。~~看造化~~
# 前置芝士
## ~~0.加 减 乘 除~~
## 1.函数
出门左转[函数 —— 百度百科](https://baike.baidu.com/item/%E5%87%BD%E6%95%B0/301912?fr=aladdin)、[人教版八下第十九章 一次函数](http://www.shuxue9.com/pep/cz8x/ebook/77.html)、[人教版高中必修 1 第一章 集合与函数概念](http://www.shuxue9.com/pep/gzbixiu1/ebook/12.html)
简单来讲,两个量 $x,y$ 如果有一种对应关系 $f$,那么这种对应关系 $f$ 就是自变量 $x$ 的函数 $f(x)$。
## 2.导数
出门右转[导数 —— 百度百科](https://baike.baidu.com/item/%E5%AF%BC%E6%95%B0/579188?fr=aladdin)、[人教版高中选修 2-2 第一章 导数及其应用](http://www.shuxue9.com/pep/gzxuanxiu22/ebook/11.html)
$$f'(x)=\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
简单来讲,在直线运动场景中,若 $x$ 表示时刻,$y$ 表示距离,函数 $f$ 表示时间与距离的关系 $y=f(x)$,那么导数 $f'(x)$ 的含义就是在第 $x$ 时刻的瞬时速度。
从某种意义上说导数的本质是一种极限,当自变量的增量无限接近 $0$ 时函数的增量与自变量的增量的比值。
从几何来看,导数是函数图像在 $(x,f(x))$ 处切线的斜率。
# $\text{Part\ 1}$ 理论知识
## 1.线性逼近!
先说一个关键问题:切线是曲线的线性逼近。
这个是什么意思呢?我们来看一看,下面是 $f(x)=x^2-1$ 的图像:
我们随便选一点 $f(x)$ 上的一点 $A(a,f(a))$ 做它的切线:

我们在 $A$ 点处放大图像:
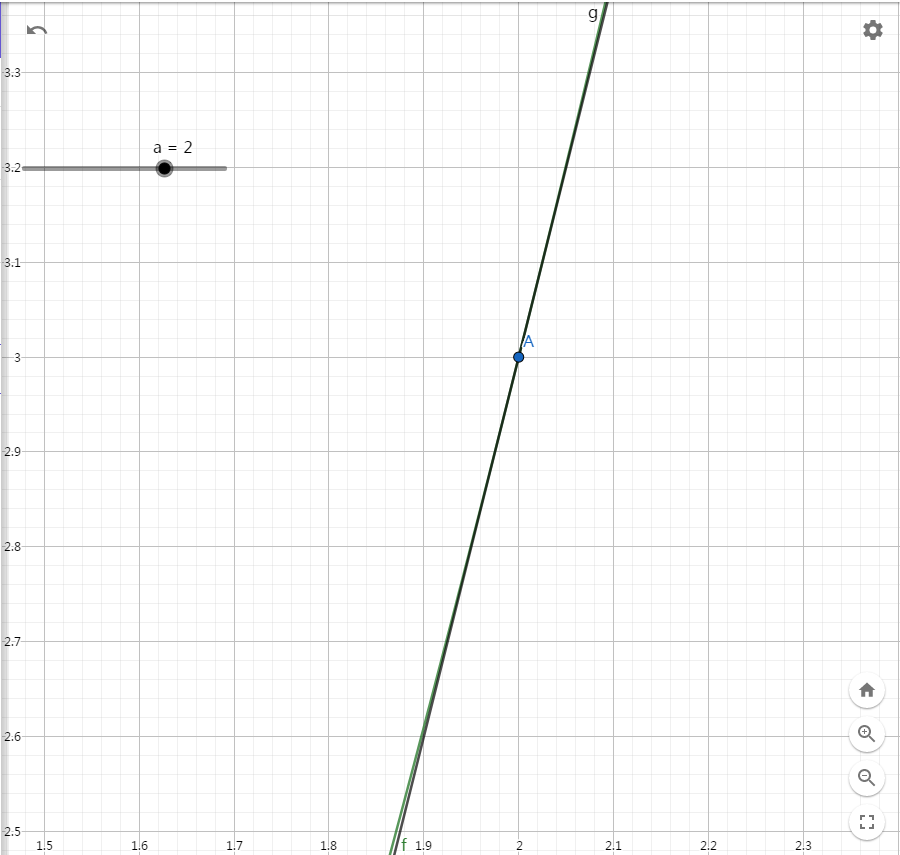
上图中,绿色的线是 $f(x)$,黑色的是 $A$ 点处的切线,可以看出放大之后切线和 $f(x)$ 非常接近了。很明显,如果我们进一步放大图像,$A$ 点切线就越接近 $f(x)$。
可以自己动手试试:
$\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/jjhfz6ca)
因为切线是一条直线,所以我们可以说,$A$ 点的切线 $g$ 是 $f(x)$ 的线性逼近。离 $A$ 点距离越近,这种逼近的效果也就越好,也就是说,切线与曲线之间的误差越小。所以我们可以说在 $A$ 点附近,“切线 $g\approx f(x)$”。
## 2.牛顿迭代?
设 $r$ 是 $f(x)$ 的根。
我们先~~随便~~选取 $x_0$ 作为 $r$ 的初始近似值,过点 $(x_0,f(x_0))$ 做切线,则与 $x$ 轴交点的横坐标 $x_1$,称 $r$ 的一次近似值。过点 $(x_1,f(x_1))$ 做切线,并求该切线与 $x$ 轴交点的横坐标 $x_2$,称为 $r$ 的二次近似值……
搞个十次八次以后得到 $x_n$,**正常**情况下 $x_n\approx r$ 了……
所以呢?没了?
~~不可能~~你教我 C++ 怎么做切线?
当然要转化为**代数式**了!
怎么转?
切线、导数、切线、导数、切数、导线……
你发现什么了吗?
~~切数和导线~~切线和导数好像是同一个东西啊……
## 3.牛顿迭代公式!
为了转化为代数式,我们可以先从特殊的情况入手。
设 $f(x)=x^2-1$,则 $f'(x)=2x$。
绘制一下函数图像:
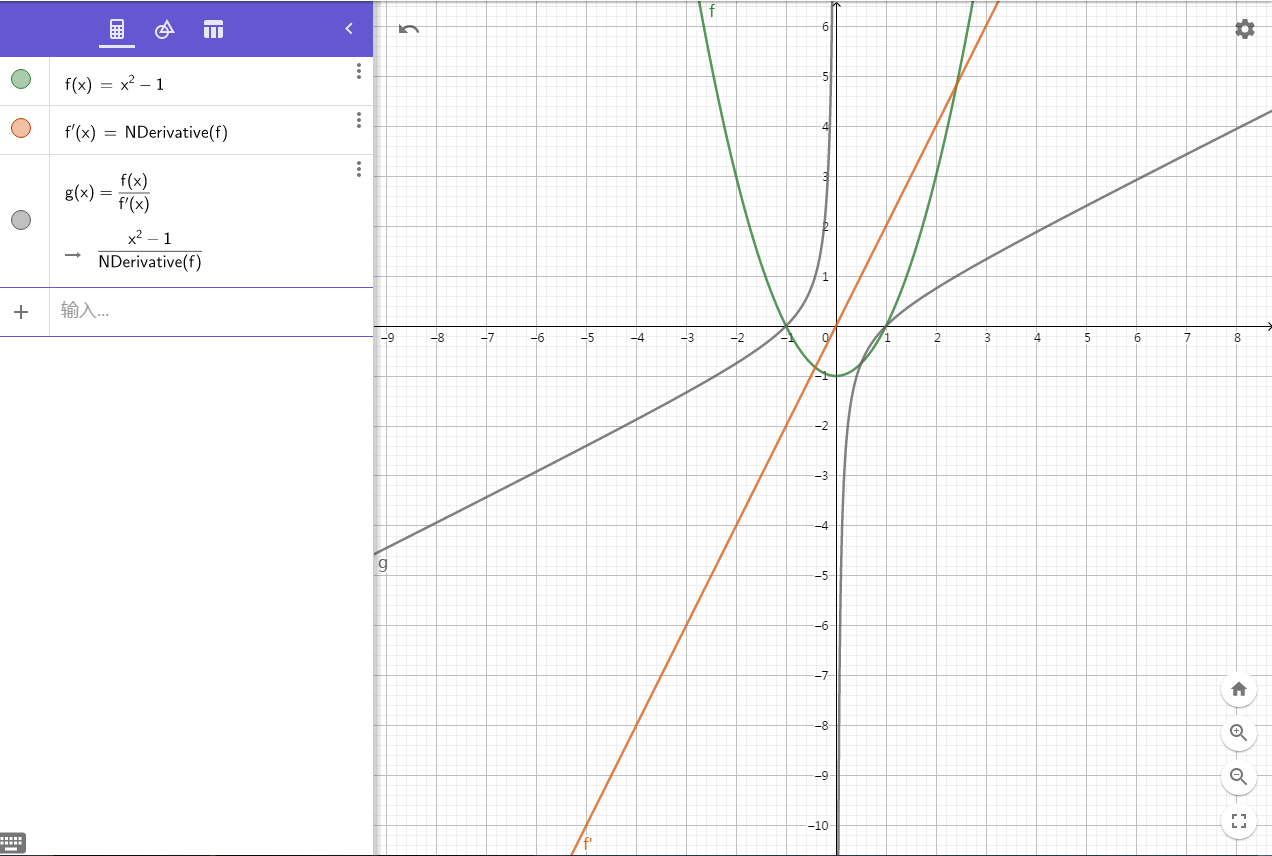
体验一下?
$\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/bezdqery)
~~显然~~,$x_n$ 点的**切线方程**为:$f(x_n)+f'(x_n)(x-x_n)$。
要求 $x_{n+1}$,即相当于求 $f(x_n)+f'(x_n)(x-x_n)=0$ 的根。
???
一个方程 $\implies$ 两个方程??
不不不。
$$f(x_n)+f'(x_n)(x_{n+1}-x_n)=0\implies x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$$
我们发现了**递推公式**!
$$\large\color{red}x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$
### 太神奇了!
## 几何意义
设 $r$ 是 $f(x)$ 的根。
我们先选取 $x_0$ 作为 $r$ 的初始近似值,过点 $(x_0,f(x_0))$ 做切线,则与 $x$ 轴交点的横坐标 $x_1$,过点 $(x_1,f(x_1))$ 做切线,并求该切线与 $x$ 轴交点的横坐标 $x_2$……
体验一下应该会理解的更加透彻。
$\text{Created\ with}$ [$\text{GeoGebra}$](https://www.geogebra.org/graphing/s7ddnkmg)
再送上维基百科动图:
## 另一个方向
回想一下泰勒展开:
$$f(x)=\lim_{n\to \infty}\sum_{i=0}^{n}\frac{f^{(n)}(x_0)}{i!}(x-x_0)^i+R_n(x)$$
我们取 $f(x)$ 的一阶泰勒展开(线性近似) $\phi(x)=f(x_0)+f'(x_0)(x-x_0)$。
我们用 $\phi(x)$ 替代 $f(x)$,那么问题转化为解 $\phi(x)=0$,即
$$f(x_0)+f'(x_0)(x-x_0)=0$$
可化为
$$x=x_0-\frac{f(x_0)}{f'(x_0)}$$
推广一下
$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$
## 模板
```cpp
inline double Newton_find_root(function f/*原函数*/)
{
const unsigned n(20);//迭代次数
double x0(x);
for (register unsigned i(1);i<=n;++i) x0-=f(x0)/f_derivative(x0);
return x0;
}
inline double Newton_find_root2(function f/*原函数*/)
{
double x0;
while (abs(f(x0))>eps) x0-=f(x0)/f_derivative(x0);
return x0;
}
```
因为牛顿迭代法是平方收敛的,最坏情况 $\Theta(\log_2 n)$。
## 适用性和弊端
它可以用来求方程的**一个根**,只要是可导函数都可以。
但是如果有多个根,就可能解出不符合题意的根,对初始值的依赖性强。
有很多坑(后面会讲)。
不过它也可以用来求极值,但是要保证有二阶导数(后面会也讲)。
# $\text{Part\ 2}$ 牛迭实战
## 1.开平方
### 给你一个正数$x$,让你用牛顿迭代法求 $\sqrt{x}$。
$$$$
$$$$
### 解答
```cpp
inline double sqrt(double x)
{
double x0(x*0.5);
while (abs(x0*x0-x)>1e-7) x0-=(x0*x0-x)/(2*x0);
return x0;
}
```
### 很简单吧,下面有点难了
## 2.$\exp
给你一个数 x,让你用牛顿迭代法求 \text e^{x}。
解答
inline double exp(double x)
{
double x0(e*x);
while (abs(log(x0)-x)>1e-7) x0-=(log(x0)-x)*x0;
return x0;
}
\text{Part\ 3} 牛迭思考
1.精确估值
牛顿迭代法的初始估值越精确,速度越快。显然
那么精确估值显得十分重要了
那么 \text{How\ to} 精确估值?
这是一个值得思考的问题。
显然函数不同,估值也不同。
来个最简单的,f(x)=x^n-a,f'(x)=nx^{n-1}。
经过我的发现,x_0=\frac{a}{n}是最接近根点的。
至于其他的,读者自己思考。明明就是你懒得想
2.求值
在\text{Part\ 2}中,我们知道了牛顿迭代法可以用来求值,那请问 f(a)=???
经过我的观察发现,要求 f(a),其实就可以通过寻找 g(x)=f^{-1}(x)-a 的根,就是 f(a)。
显然,g'(x)=(f^{-1}(x))'。
设 y=f^{-1}(x),f(y)=x,
则 f'(y)=x'=1,所以 \frac{df(y)}{dy}\cdot\frac{dy}{dx}=1,所以 (f^{-1}(x))'=(f'(y))^{-1}
3.bug???
3.1.驻点???
起始点不幸选择了驻点,从几何上看切线 \parallel x 轴,根本没有根。
从代数上看,x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}} 没有意义(f'(x_{n})=0)。
3.2.不收敛???
下面是 f(x)=\sqrt[3]{x}:
我们发现不论怎么选择起始点,越迭代就越远离根点。
从代数上看
x_{n+1}=x_n-\frac {f(x_n)}{f'(x_n)}=x_n-\frac{\sqrt[3]{x_n}}{\frac{1}{3}x^{-\frac{2}{3}}}=-2x_n
就是说下一个点比上一个点更远离根点。
此处根显然是0,但是f'(0)=0,无法迭代。
天理不容啊!!!
3.3.循环震荡???
还有一种更酸爽的不收敛,就是不断的循环震荡。
比如下面是 f(x)=\sqrt{|x|} 的曲线:
从代数上看
x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=x_n-2x_n=-x_n
由于选择的起始点不对,造成这种循环的情况其实还挺多,在很多曲线的某些点都会出现这种情况。
3.4.\text{无法迭代???}
有一天,%%%LCX 大佬突发奇想,想用牛顿迭代法求平方,他的思路是这样的:
a^2\implies\text{解}\ \sqrt{x}-a=0
\text{设}\ f(x)=\sqrt{x}-a,f'(x)=\frac{1}{2\sqrt{x}}
x_{n+1}=x_n-\frac{\sqrt{x_n}-a}{\frac{1}{2\sqrt{x_n}}}=x_n-2\sqrt{x_n}(\sqrt{x_n}-a)=x_n-2x_n+2a\sqrt{x_n}=2a\sqrt{x_n}-x_n
他兴高采烈地打出了程序,然而……
\Large\color{red}\text{炸了!!!}
他叫我过去帮他检查一下,发现出现了负数开平方或0的情况……
\text{Why???}
下面是f(x)=\sqrt{x}-2的曲线:
一般情况是这样的 (0<x_0<16):
二般情况是这样的(负数开平方)(x_0>16):
三般情况是这样的(0 发生了循环 ,x_0=16):
感受一下?
由于选择的起始点不对,造成这种情况其实还挺多……
~~不过求算数平方根可没这么坑。~~
~~ZXJ:“LCX 叫你作死,叫你作死,傻了吧哈哈哈哈哈哈哈……”~~
# $\text{Part\ 4}$ 应用于最优化问题
牛顿法也被用于求函数的极值。
因为导数的物理定义是物体的瞬时速度,所以函数极值点处的导数值为零。
因此导函数的零点就是原函数的极值点。
因此我们要求原函数的极值点,我们可以使用牛顿迭代法找到导函数的零点。
递推式如下:
$$\large\color{red}x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}$$
# $\text{Part\ 5}$ 推广
刚才我们学习了牛顿迭代法,不过这只是一元函数,对于多元函数$f(x)$,我们只需要将一元函数牛顿迭代法中的 $f'(x)$ 改为 $\nabla f=\{\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}\}$,就是梯度,是一个向量,所以结果也是向量。
在高维下,$\phi(x)=f(x_0)+\nabla f(x_0)^T(x-x_0)$。
解 $\phi(x)=0$。
递推公式为:
$$x_{n+1}=x_n-f(x_n)\nabla f(x_n)^T$$
不过这计算很慢,优化的方法有 DFP,BFGS,Broyden 等。
# $\text{Part\ 6}$ 小结
既然你看到了这里,一般来说牛顿迭代法你已经 get 到了。
其实核心就是一个式子:
$$\Large\color{red}x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$
非常简洁。
~~如果你累了,可以退出。~~
还有其实牛顿迭代法在 $\text{OI}$ 中的主要应用还是解方程,求解多项式问题,极值问题等。
$$\Large\color{purple}\text{牛顿迭代法完结撒花!!!}$$
$$$$
$$$$
$$$$
$$$$
$$$$
# 新的思考?
有一些~~变态的~~函数,$f(x)$ 十分简单,但是 $f'(x)$,不易算出,或是过于复杂。~~不符合毒瘤出题人的审美~~
比如:……~~(作者找不到栗子……)~~
为了避免计算麻烦的 $f'(x)$,自然有大佬改变方法……
# 割线法!!!
**割线法的基本思想是用*弦的斜率*近似代替*切线斜率*,并用割线与横轴交点的横坐标作为方程式的根的近似。**
## 具体步骤
$f(x)$ 上~~随便~~找两点 $(x_n,f(x_n))$ 和 $(x_{n-1},f(x_{n-1}))$,两点所在的**直线**就是割线,~~显然~~直线方程为:
$$y-f(x_n)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}(x-x_n)$$
???
一个方程 $\implies$ 两个方程??
不不不。
$$y-f(x_n)=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}(x-x_n)\implies x=x_n+\frac{(y-f(x_n))(x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}$$
我们要求割线与横轴交点的横坐标,设为 $x_{n+1}$。
~~显然~~ $x_{n+1}\approx x,y=0$。
$$\therefore \color{red}x_{n+1}=x_n-\frac{f(x_n)(x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}$$
据说它收敛更快???平方收敛???
$$\Large\color{purple}\text{割线法完结撒花!!!}$$
$$$$
$$$$
$$$$
$$$$
$$$$
# 题外话 —— 平方根倒数速算法(卡马克开方法)
这有悠久的历史……
平方根倒数速算法是适用于快速计算平方根的倒数(符合 IEEE 754 标准格式的 32 位浮点数)的一种算法,于 1999 年在《雷神之锤 III 竞技场》的源代码中应用。
此算法首先接收一个**32 位带符浮点数**,然后将之作为一个**32 位整数**看待,以将其向右进行一次逻辑移位的方式将之**取半**,并用 `0x5f3759df` 减之,如此即可得首次近似值,以牛顿法反复迭代,以求出更精确的近似值。在计算浮点数的平方根倒数的同一精度的近似值时,此算法比直接使用浮点数除法要**快四倍**。
上源码:
```cpp
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
```
后来,$\text{Chris\ Lomont}$ 大佬站了出来,他找到了一个更加精确的数字`0x5f375a86`。
(相关资料[戳我](https://diducoder.com/sotry-about-sqrt.html))
后来,又有大佬站了出来,他找到了 **64 位**的 IEEE754 浮点数(即**双精度类型**)所对应的魔术数字是 `0x5fe6eb50c7aa19f9`。
## 原理???
~~我也不知道……会用就行。~~
可以参考这篇文章 —— [揭秘·变态的平方根倒数算法](https://segmentfault.com/a/1190000006170378)
$$$$
$$$$
$$$$
$$$$
$$$$
$$\Huge\color{purple}\text{完结撒花!!!}$$
$$$$
$$$$
$$$$
$$$$
$$$$
# 参考资料
- [牛顿法_百度百科](https://baike.baidu.com/item/牛顿法/1384129?fr=aladdin)
- [如何通俗易懂地讲解牛顿迭代法?——马同学高等数学](https://www.matongxue.com/madocs/205/)
- [割线法_百度百科](https://baike.baidu.com/item/割线法/5806354?fr=aladdin)
- [平方根倒数速算法_百度百科](https://baike.baidu.com/item/平方根倒数速算法/4075273?fr=aladdin)
- [揭秘·变态的平方根倒数算法](https://segmentfault.com/a/1190000006170378)
- [一个 sqrt 函数引发的血案](https://diducoder.com/sotry-about-sqrt.html)
# 后记
感觉自己好菜啊……
希望这篇文章对你有用。
在这之后,我还会写一下其他常用的最优化算法。
等着吧……
还有,牛顿迭代法不是线性近似(一阶泰勒展开)吗?那我用二阶泰勒展开岂不是更好?