AT_agc004_f [AGC004F] Namori
题目描述
给定一个由 $N$ 个顶点和 $M$ 条边构成的无向图。其中,$N-1 \le M \le N$,且图连通。此外,图中没有自环和重边。
顶点编号为 $1$ 到 $N$,边编号为 $1$ 到 $M$。边 $i$ 连接顶点 $a_i$ 和 $b_i$。
每个顶点可以被染成白色或黑色。初始时,所有顶点都是白色的。你需要通过进行以下操作若干次,将所有顶点变为黑色:
+ 选择一对相邻(位于同一条边的两端)的同色顶点,将它们颜色同时反转。即,若均为白色则变为黑色,若均为黑色则变为白色。
请判断是否可以将所有顶点变为黑色,如果可以,输出所需的最小操作次数;否则输出 `-1`。
输入格式
输入格式如下:
> $ N $ $ M $
> $ a_1 $ $ b_1 $
> $ a_2 $ $ b_2 $
> $ : $
> $ a_M $ $ b_M $
输出格式
如果可以将所有顶点变为黑色,输出所需的最小操作次数;否则输出 `-1`。
说明/提示
### 数据范围与约定
+ $2 \le N \le 10^5$
+ $N-1 \le M \le N$
+ $1 \le a_i, b_i \le N$
+ 图中没有自环和重边。
+ 图是连通的。
### 部分分
+ 在 $1500$ 分的测试数据中,满足 $M = N-1$。
### 样例解释 #1
例如,可以按照图示的方式进行操作。
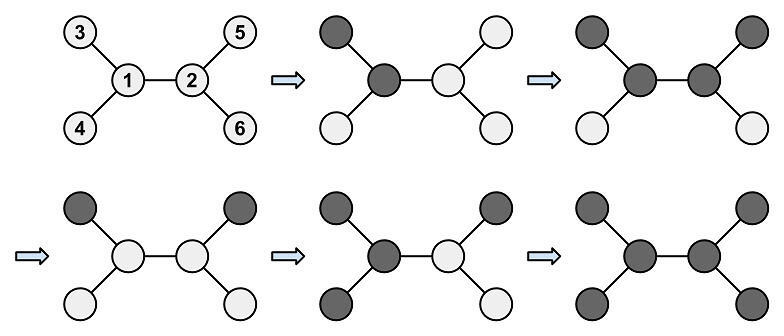
### 样例解释 #2
无法将所有顶点变为黑色。
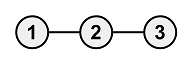
### 样例解释 #3
此样例不被包含在部分分的测试数据中。
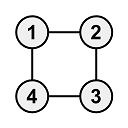
### 样例解释 #4
此样例不被包含在部分分的测试数据中。