AT_agc005_e [AGC005E] Sugigma: The Showdown
题目描述
しぐま君和すぎむ君决定玩一个游戏。
这个游戏在一个有 $N$ 个顶点的图上进行。顶点编号为 $1,2,\ldots,N$。图中有 $N-1$ 条红色边和 $N-1$ 条蓝色边,且这两组边各自都构成一棵树。红色边由 $(a_i, b_i)$ 表示,蓝色边由 $(c_i, d_i)$ 表示。
两人各自有一个棋子,しぐま君的棋子初始在顶点 $X$,すぎむ君的棋子初始在顶点 $Y$。
游戏按回合进行,第 $1$、$3$、$5$、……回合由しぐま君行动,第 $2$、$4$、$6$、……回合由すぎむ君行动。
每个人在自己的回合可以选择移动自己的棋子或选择不动。但移动时有如下限制:しぐま君只能沿红色边移动到相邻顶点,すぎむ君只能沿蓝色边移动到相邻顶点。
如果两枚棋子到达同一个顶点,游戏立即结束。如果在第 $i$ 回合操作后游戏结束,则总回合数为 $i$。
しぐま君希望让总回合数尽可能大,すぎむ君希望让总回合数尽可能小。
假设两人都以各自的目标采取最优策略,请判断游戏是否一定会结束。如果会结束,输出总回合数;如果永远不会结束,输出 $-1$。
输入格式
输入按以下格式从标准输入读入。
> $N\ X\ Y\ a_1\ b_1\ a_2\ b_2\ :\ a_{N-1}\ b_{N-1}\ c_1\ d_1\ c_2\ d_2\ :\ c_{N-1}\ d_{N-1}$
输出格式
输出一行答案。如果游戏永远不会结束,输出 $-1$。
说明/提示
## 限制条件
- $2 \leq N \leq 200,\!000$
- $1 \leq X, Y \leq N$
- $X \neq Y$
- $1 \leq a_i, b_i, c_i, d_i \leq N$
- 红色边和蓝色边各自都构成一棵树
## 样例解释 1
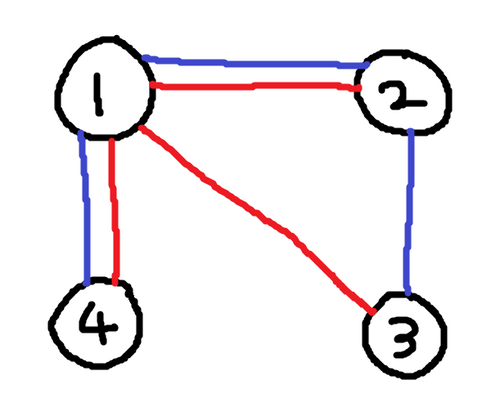
## 样例解释 2
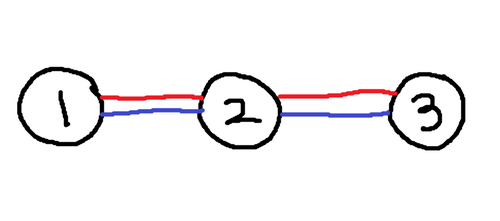
## 样例解释 3
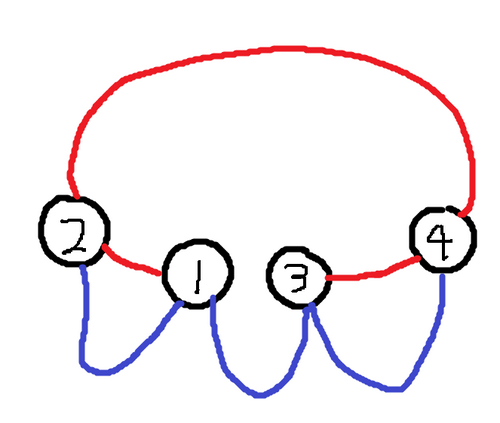
由 ChatGPT 4.1 翻译