AT_arc062_d [ARC062F] AtCoDeerくんとグラフ色塗り

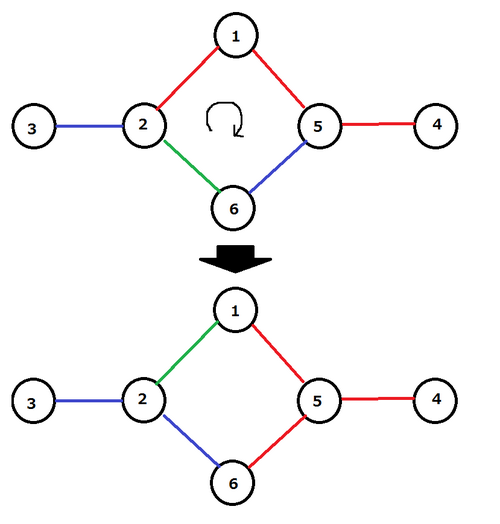
有一天，鹿的 AtCoDeer 君捡到了一张由 $N$ 个顶点、$M$ 条边组成的简单图（即没有重边和自环）。顶点编号为 $1,2,\ldots,N$，彼此可以区分，边用 $(a_i,b_i)\ (1\leq i\leq M)$ 表示。AtCoDeer 君打算用 $K$ 种颜色的油漆给每条边涂色。油漆数量充足，因此可以用同一种颜色涂多条边。 由于 AtCoDeer 君捡到的图有特殊的形状，他可以选择一个简单环（即每个顶点只经过一次的环），并将该环上的边的颜色沿着环依次轮换。具体来说，设环上的边依次为 $e_1, e_2, \ldots, e_a$，则可以将 $e_1$ 的颜色涂到 $e_2$，$e_2$ 的颜色涂到 $e_3$，……，$e_{a-1}$ 的颜色涂到 $e_a$，$e_a$ 的颜色涂到 $e_1$，同时进行涂色替换。  图 $1$：操作示例 如果通过有限次上述操作，可以将涂色方案 A 变换为涂色方案 B，则认为这两种涂色方案是相同的。请你求出不同的涂色方案有多少种。由于答案可能非常大，请输出对 $10^9+7$ 取模的结果。

输入通过标准输入给出，格式如下： > $N$ $M$ $K$ $a_1$ $b_1$ $a_2$ $b_2$ $\ldots$ $a_M$ $b_M$

输出不同的涂色方案数对 $10^9+7$ 取模的结果。

## 限制条件 - $1\leq N\leq 50$ - $1\leq M\leq 100$ - $1\leq K\leq 100$ - $1\leq a_i,b_i\leq N\ (1\leq i\leq M)$ - 图中没有自环和重边。 由 ChatGPT 4.1 翻译