AT_abc047_b [ABC047B] すぬけ君の塗り絵 2 イージー
题目描述
在 $xy$ 平面上,有一个左下角坐标为 $(0, 0)$,右上角坐标为 $(W, H)$,且各边平行于 $x$ 轴或 $y$ 轴的长方形。最初,长方形的内部被涂成白色。
すぬけ君在这个长方形内打了 $N$ 个点。第 $i$ 个点($1 \leq i \leq N$)的坐标为 $(x_i, y_i)$。
此外,すぬけ君还确定了一个长度为 $N$ 的数列 $a$,对于每个 $1 \leq i \leq N$:
- 当 $a_i = 1$ 时,将长方形内满足 $x < x_i$ 的区域涂黑;
- 当 $a_i = 2$ 时,将长方形内满足 $x > x_i$ 的区域涂黑;
- 当 $a_i = 3$ 时,将长方形内满足 $y < y_i$ 的区域涂黑;
- 当 $a_i = 4$ 时,将长方形内满足 $y > y_i$ 的区域涂黑。
请你求出涂色结束后,长方形内剩余白色部分的面积。
输入格式
输入以如下格式从标准输入读入:
> $W$ $H$ $N$ $x_1$ $y_1$ $a_1$ $x_2$ $y_2$ $a_2$ $\ldots$ $x_N$ $y_N$ $a_N$
输出格式
输出涂色结束后长方形内剩余白色部分的面积。
说明/提示
## 限制条件
- $1 \leq W, H \leq 100$
- $1 \leq N \leq 100$
- $0 \leq x_i \leq W$($1 \leq i \leq N$)
- $0 \leq y_i \leq H$($1 \leq i \leq N$)
- $W$、$H$(21:32 补充)、$x_i$、$y_i$ 均为整数
- $a_i$($1 \leq i \leq N$)为 $1, 2, 3, 4$ 之一
## 样例解释 1
すぬけ君开始涂色前的长方形如下图所示。
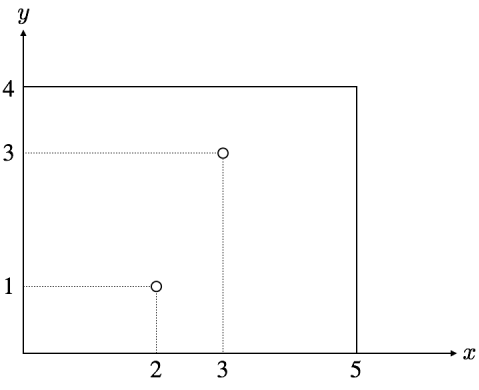
$(x_1, y_1) = (2, 1)$,$a_1 = 1$,所以首先すぬけ君将 $x$ 坐标小于 $2$ 的区域涂黑,长方形变为如下所示。
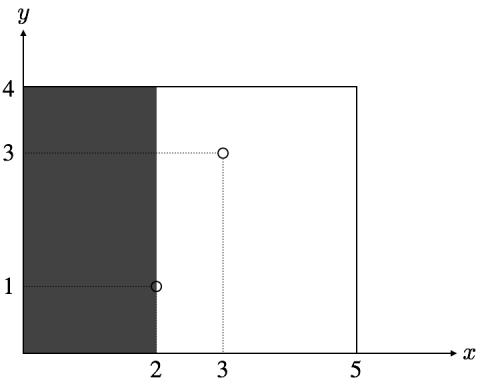
$(x_2, y_2) = (3, 3)$,$a_2 = 4$,接着すぬけ君将 $y$ 坐标大于 $3$ 的区域涂黑,长方形最终如下所示。

最终白色部分的面积为 $9$,因此输出为 $9$。
## 样例解释 2
涂色结果也有可能没有剩余白色部分。
由 ChatGPT 4.1 翻译