AT_agc009_b [AGC009B] Tournament

有 $N$ 个人参加了一场比赛。这场比赛采用淘汰赛制，总共进行了 $N-1$ 场比赛。由于各种原因，这个淘汰赛的赛程并不一定对所有参赛者都是公平的。也就是说，每个人为了获得冠军所需的胜场数并不一定相同。淘汰赛的结构将在题目末尾正式定义。 每场比赛必定有一方获胜，另一方失败，最终未曾输过的那个人获得冠军。 下图是一个淘汰赛的例子：  每个人编号为 $1$ 到 $N$，其中 $1$ 号选手获得了冠军，除了冠军以外的每个选手 $i$（$2 \leq i \leq N$）都在与 $a_i$ 号选手的比赛中输掉了比赛。 淘汰赛的深度定义为：对于所有选手，为了获得冠军所需的胜场数的最大值。 请你求出可能的最小淘汰赛深度。 淘汰赛的结构正式定义如下。在第 $i$ 场比赛中： - 由预先指定的两名尚未参加过比赛的选手进行比赛； - 或由预先指定的一名尚未参加过比赛的选手与第 $j$ 场比赛（$j < i$）的获胜者进行比赛； - 或由预先指定的第 $j$ 场（$j < i$）和第 $k$ 场（$k < i, j \neq k$）的获胜者进行比赛。 上述三种情况中任选其一的两人进行比赛。只要无论比赛结果如何，都不会出现已经输过比赛的人再次参赛的情况，这样的结构就称为淘汰赛。

输入通过标准输入给出，格式如下： > $N$ $a_2$ $a_3$ ... $a_N$

输出可能的最小淘汰赛深度。

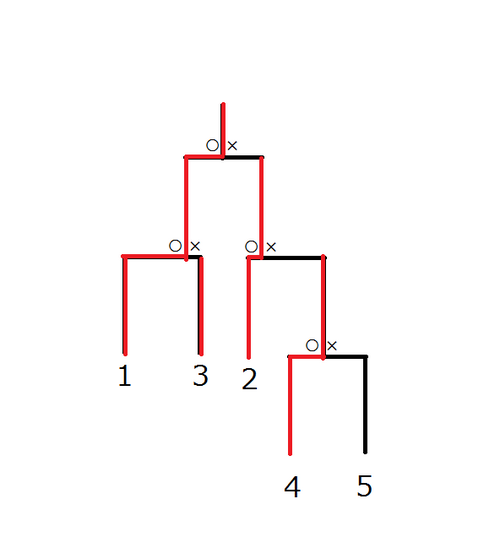
## 限制条件 - $2 \leq N \leq 10^5$ - $1 \leq a_i \leq N\ (2 \leq i \leq N)$ - 存在与输入比赛结果相符的淘汰赛结构 ## 样例解释 1 以下是满足条件的比赛结果： - 第 1 场比赛，4 号与 5 号选手对战，4 号获胜 - 第 2 场比赛，2 号与 4 号选手对战，2 号获胜 - 第 3 场比赛，1 号与 3 号选手对战，1 号获胜 - 第 4 场比赛，1 号与 2 号选手对战，1 号获胜  在这个淘汰赛中，5 号选手若要获得冠军需要赢下 3 场比赛，因此淘汰赛的深度为 3。反之，不存在深度不超过 2 且满足条件的淘汰赛，因此输出 3。 由 ChatGPT 4.1 翻译