AT_agc013_e [AGC013E] Placing Squares
题目描述
joisinoお姉ちゃん有一根长度为 $N$ 的木棒。这根木棒上有 $M$ 个标记。第 $i$ 个标记位于木棒左端向右第 $X_i$ 的位置。
joisinoお姉ちゃん打算在这根木棒上放置若干个正方形。放置正方形需要满足以下条件:
- 只能放置边长为整数的正方形。
- 所有正方形都必须以底边与木棒对齐的方式放置。
- 所有正方形需要将木棒完全覆盖。也就是说,正方形不能超出木棒的边界,也不能有木棒的部分没有被正方形上方覆盖。
- 木棒有标记的地方不能正好在两个正方形的边界处。
下图中给出了满足条件和不满足条件的正方形摆放示例。
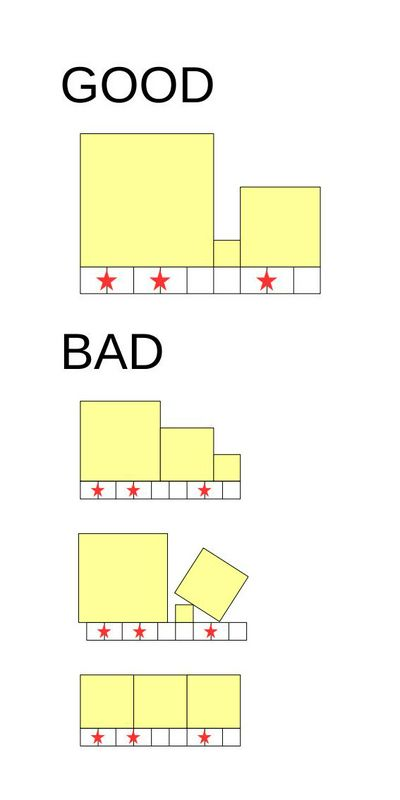
对于一种正方形的摆放方案,它的“美丽度”定义为所有正方形面积的**乘积**。joisinoお姉ちゃん想要知道,满足上述条件的所有正方形摆放方案的美丽度之和是多少。你的任务是帮她写一个程序,计算出这个总和,并对 $10^9+7$ 取模后输出。
输入格式
输入为一行,格式如下:
> $N$ $M$ $X_1$ $X_2$ $\cdots$ $X_{M-1}$ $X_M$
输出格式
请输出所有可能的正方形摆放方案的美丽度之和,对 $10^9+7$ 取模。
说明/提示
## 限制条件
- 输入均为整数
- $1 \leq N \leq 10^9$
- $0 \leq M \leq 10^5$
- $1 \leq X_1 < X_2 < \dots < X_{M-1} < X_M \leq N-1$
## 样例解释 1
可能的方案有以下两种:
- 左边放一个边长为 $1$ 的正方形,右边放一个边长为 $2$ 的正方形
- 放一个边长为 $3$ 的正方形
因此,美丽度之和为 $(1 \times 1 \times 2 \times 2) + (3 \times 3) = 13$。
由 ChatGPT 5 翻译