AT_arc071_b [ABC058D] ###

在二维平面上，有 $m$ 条与 $x$ 轴平行的直线和 $n$ 条与 $y$ 轴平行的直线。第 $i$ 条从下往上的与 $x$ 轴平行的直线可以表示为 $y = y_i$。第 $i$ 条从左往右的与 $y$ 轴平行的直线可以表示为 $x = x_i$。 请计算所有存在于这些直线中的长方形的面积和，并输出其对 $10^9+7$ 取模的结果。 也就是说，对于所有满足 $1 \leq i < j \leq n$ 且 $1 \leq k < l \leq m$ 的组合 $(i, j, k, l)$，考虑由直线 $x = x_i$、$x = x_j$、$y = y_k$、$y = y_l$ 围成的长方形，求这些长方形的面积的总和，并输出其对 $10^9 + 7$ 取模的结果。

输入按以下格式从标准输入读入。 > $n$ $m$ $x_1$ $x_2$ $\ldots$ $x_n$ $y_1$ $y_2$ $\ldots$ $y_m$

请输出所有长方形的面积总和对 $10^9+7$ 取模后的值，占一行输出。

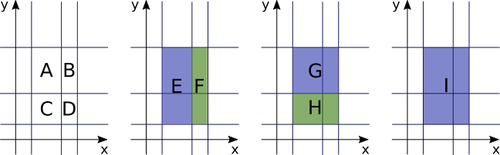
### 数据范围 - $2 \leq n, m \leq 10^5$ - $-10^9 \leq x_1 < \ldots < x_n \leq 10^9$ - $-10^9 \leq y_1 < \ldots < y_m \leq 10^9$ - $x_i, y_i$ 均为整数 ### 样例解释 1 将此输入画成图像如下所示。  把长方形 A、B、...、I 的面积全部加总，结果为 $60$。  由 ChatGPT 5 翻译