AT_arc078_d [ARC078F] Mole and Abandoned Mine

鼹鼠决定住在一个废弃矿井中，该矿井可以表示为一个包含编号为 $1$ 到 $N$ 的 $N$ 个顶点和 $M$ 条边的简单连通无向图。第 $i$ 条边连接顶点 $a_i$ 和 $b_i$，移除这条边需要 $c_i$ 日元。 鼹鼠希望通过移除一些边，使得从顶点 $1$ 到顶点 $N$ 的路径仅有一条，并且在路径上不经过同一个顶点两次。请计算实现这一目标所需的最小资金。

输入以以下格式从标准输入中给出。 > $N$ $M$ > $a_1$ $b_1$ $c_1$ > $\vdots$ > $a_M$ $b_M$ $c_M$

请输出答案。

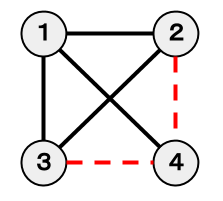
## 限制条件 - $2 \leq N \leq 15$ - $N-1 \leq M \leq N(N-1)/2$ - $1 \leq a_i, b_i \leq N$ - $1 \leq c_i \leq 10^6$ - 给定的图中不存在重边或自环 - 给定的图是连通图 ## 样例解释 1 在下图中，用红色虚线表示被移除的边。按照该图的方式移除两条边，总共需要 $200$ 日元。  ## 样例解释 2 有时从一开始，顶点 $1$ 到顶点 $N$ 的路径就只有一种。 由 ChatGPT 5 翻译