AT_ddcc2020_qual_c Strawberry Cakes

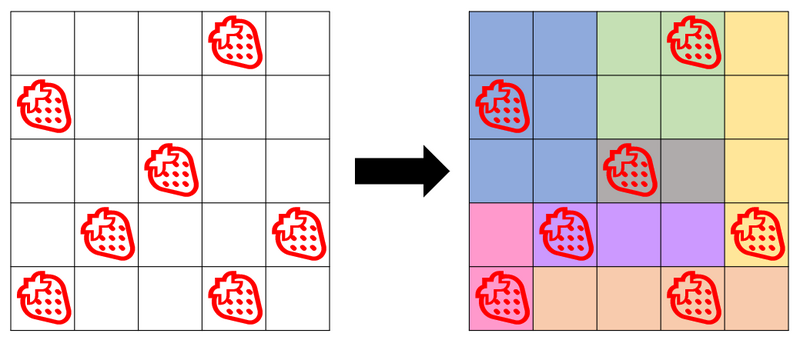
chokudai 在 DDCC 2020 本赛中为参赛者准备了一个长方形的蛋糕。 这个蛋糕通过 $H-1$ 条横向切缝和 $W-1$ 条纵向切缝，被等分成了 $H \times W$ 个区域。在这些区域中，有 $K$ 个区域各放有一个草莓。 草莓的位置由 $H \times W$ 个字符 $s_{i,j}$（$1 \leq i \leq H, 1 \leq j \leq W$）给出。当 $s_{i,j}$ 为 `#` 时，表示从上往下第 $i$ 行、从左往右第 $j$ 列的区域有一个草莓；当 $s_{i,j}$ 为 `.` 时，表示该区域没有草莓。字符 `#` 恰好出现 $K$ 次。 现在，chokudai 想要沿着切缝将蛋糕切成 $K$ 块，并分发给参赛者。切分后，每一块都必须满足以下条件： - 形状为长方形。 - 恰好包含 $1$ 个草莓。 例如，下图是一个可能的切分方式。  请你求出一种满足条件的蛋糕切分方式。无论草莓的数量和位置如何，总能找到一种切分方式。

输入以如下格式从标准输入读入。 > $H$ $W$ $K$ > $s_{1,1} s_{1,2} \cdots s_{1,W}$ > $s_{2,1} s_{2,2} \cdots s_{2,W}$ > $\vdots$ > $s_{H,1} s_{H,2} \cdots s_{H,W}$

请为切分后的 $K$ 块蛋糕任意编号为 $1,2,3,\dots,K$，并输出一个 $H \times W$ 的矩阵。矩阵中第 $i$ 行第 $j$ 列的数字 $a_{i,j}$ 表示该区域属于哪一块蛋糕。 > $a_{1,1} a_{1,2} \cdots a_{1,W}$ > $a_{2,1} a_{2,2} \cdots a_{2,W}$ > $\vdots$ > $a_{H,1} a_{H,2} \cdots a_{H,W}$ 如果存在多种切分方式，输出其中任意一种即可。

### 数据范围 - $1 \leq H \leq 300$ - $1 \leq W \leq 300$ - $1 \leq K \leq H \times W$ - $s_{i,j}$ 为 `#` 或 `.` - `#` 在 $s$ 中恰好出现 $K$ 次 ### 样例解释 1 例如，下图展示了一种切分方式。  ### 样例解释 2 例如，下图展示了一种切分方式。  由 ChatGPT 4.1 翻译