AT_abc008_3 [ABC008C] コイン
题目描述
高桥君有 $N$ 枚可以区分正反面的硬币。每枚硬币的大小不同,每枚硬币上都写有一个正整数。
他将这些硬币随机(所有 $N!$ 种排列出现的概率相同)排成一行。然后,执行以下操作:
1. 将所有硬币翻到正面朝上。
2. 从左到右依次处理每一枚硬币,对于当前正在看的硬币,找到其右侧(不包括自身)所有硬币中,硬币上所写整数是当前硬币上整数的倍数的那些硬币,将它们全部翻面。
高桥君想知道,操作结束后正面朝上的硬币数量的期望值。
请你帮高桥君编写程序,计算这个期望值。
输入格式
输入通过标准输入给出,格式如下:
> $N$
> $C_1$
> $C_2$
> $\vdots$
> $C_N$
- 第 $1$ 行为一个整数 $N$,表示硬币的数量,$1 \leq N \leq 100$。
- 接下来的 $N$ 行,第 $i$ 行为一个整数 $C_i$,表示第 $i$ 枚硬币上写的正整数,$1 \leq C_i \leq 10^9$。
输出格式
输出操作结束后正面朝上的硬币数量的期望值。绝对误差或相对误差不超过 $10^{-6}$ 即可。输出末尾需换行。
说明/提示
## 部分分
本题设置了部分分。
- 对于满足 $N \leq 8$ 的数据集 1,答对可得 $99$ 分。
- 对于无额外限制的数据集 2,答对可再得 $1$ 分,满分 $100$ 分。
## 样例解释 1
硬币上从小到大分别写着 $2$、$4$、$8$。例如,在 $3!$ 种排列中,若硬币按大小升序排列,则操作如下:
1. 初始时,所有硬币正面朝上,状态为 $[\text{正}, \text{正}, \text{正}]$。
2. 接着,在左起第 $2$ 个及其右侧的硬币中,查找写有 $2$ 的倍数的硬币。左起第 $2$ 个和第 $3$ 个硬币满足条件,将它们翻面,状态变为 $[\text{正}, \text{反}, \text{反}]$。
3. 然后,在左起第 $3$ 个及其右侧的硬币中,查找写有 $4$ 的倍数的硬币。只有左起第 $3$ 个硬币满足条件,将其翻面,状态变为 $[\text{正}, \text{反}, \text{正}]$。
硬币正反变化如下图所示,白色为正面,黑色为反面。
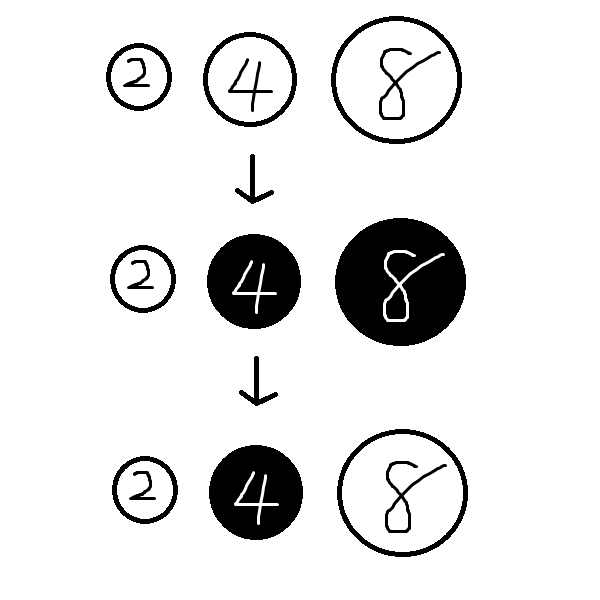
对于全部 $3! = 6$ 种排列,每种排列下最终状态如下图所示。
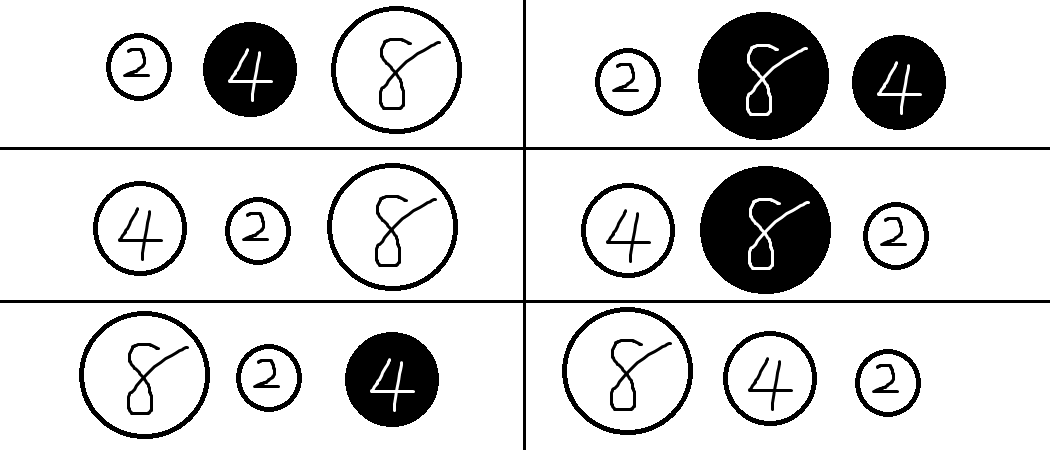
因此,期望值为 $13/6 = 2.16666666666\ldots$。
## 样例解释 2
无论排列顺序如何,最终状态总是 $[\text{正}, \text{反}, \text{正}, \text{反}]$。
由 ChatGPT 4.1 翻译