AT_abc008_4 [ABC008D] 金塊ゲーム

[problemUrl]: https://atcoder.jp/contests/abc008/tasks/abc008_4 高橋君はとあるゲームをプレイしている。このゲームでは縦横方向に無限に広がるマス目の上で行われる。各マス目は正方形状で、各辺は東西方向または南北方向に平行である。マス目のうちあるマスには ($ 0 $,$ 0 $) という数字の組が割り当てられており、このマスから東方向に $ x $ マス ($ x\ のときは西方向に\ -x $ マス)進み、北方向に $ y $ マス ($ y\ のときは南方向に\ -y $ マス)進んだところにあるマスには ($ x $,$ y $) という数字の組が割り当てられている。 マス目上には $ W $ × $ H $ 個の金塊がある。これらの金塊は $ 1 $ ≦ $ p $ ≦ $ W $ かつ $ 1 $ ≦ $ q $ ≦ $ H $ を満たすすべてのマス ($ p $,$ q $) に $ 1 $ 個ずつ置かれている。また、金塊があるマスのうちちょうど $ N $ マスには金塊回収装置がある。装置には $ 1 $ から $ N $ までの番号が付いている。どの $ 2 $ つのマス ($ a $,$ b $) , ($ c $,$ d $) に関しても、$ 2 $ つのマスの両方に装置があるならば、$ a≠c $ かつ $ b≠d $ である。また、複数の装置が同じマスにあることはない。最初、どの金塊回収装置も作動していない。 金塊回収装置は作動すると、まずは装置のあるマスにある金塊を回収する。その後、東西南北それぞれの方向にクレーンを伸ばすことで更に金塊を回収することができる。クレーンの性質上、クレーンを下ろす場所には金塊がなく、かつ回収する区間では金塊が連続して存在していなければならない。つまり、クレーンのあるマスを ($ x $,$ y $) としたとき、以下に示す条件でのみクレーンを下ろし、金塊を回収することができる。 - 東方向に回収する処理：次の条件を満たす整数 $ p $ を選ぶ。その後、$ x+1 $ ≦ $ i $ ≦ $ p-1 $ を満たすすべてのマス ($ i $,$ y $) の金塊を回収する。 > - 条件：$ p $ > $ x+1 $ であり、$ x+1 $ ≦ $ i $ ≦ $ p-1 $ を満たすすべてのマス ($ i $,$ y $) に金塊があり、かつマス ($ p $,$ y $) に金塊がない。 - 西方向に回収する処理：次の条件を満たす整数 $ p $ を選ぶ。その後、$ p+1 $ ≦ $ i $ ≦ $ x-1 $ を満たすすべてのマス ($ i $,$ y $) の金塊を回収する。 > - 条件：$ p $ x-1 であり、$ p+1 $ ≦ $ i $ ≦ $ x-1 $ を満たすすべてのマス ($ i $,$ y $) に金塊があり、かつマス ($ p $,$ y $) に金塊がない。 - 南方向に回収する処理：次の条件を満たす整数 $ q $ を選ぶ。その後、$ q+1 $ ≦ $ j $ ≦ $ y-1 $ を満たすすべてのマス ($ x $,$ j $) の金塊を回収する。 > - 条件：$ q $ y-1 であり、$ q+1 $ ≦ $ j $ ≦ $ y-1 $ を満たすすべてのマス ($ x $,$ j $) に金塊があり、かつマス ($ x $,$ q $) に金塊がない。 - 北方向に回収する処理：次の条件を満たす整数 $ q $ を選ぶ。その後、$ y+1 $ ≦ $ j $ ≦ $ q-1 $ を満たすすべてのマス ($ x $,$ j $) の金塊を回収する。 > - 条件：$ q $ > $ y+1 $ であり、$ y+1 $ ≦ $ j $ ≦ $ q-1 $ を満たすすべてのマス ($ x $,$ j $) に金塊があり、かつマス ($ x $,$ q $) に金塊がない。 それぞれの方向に関して、条件を満たす $ p $ または $ q $ が存在しない場合は、その方向にクレーンを伸ばすことができない。 また、それぞれの方向に関して、金塊を回収可能ならば、必ず回収しなければならない。下に条件を満たす回収方法の一例を示す。ただし、以降の図において装置を `M` の記号で表し、回収可能な範囲は太枠で表している。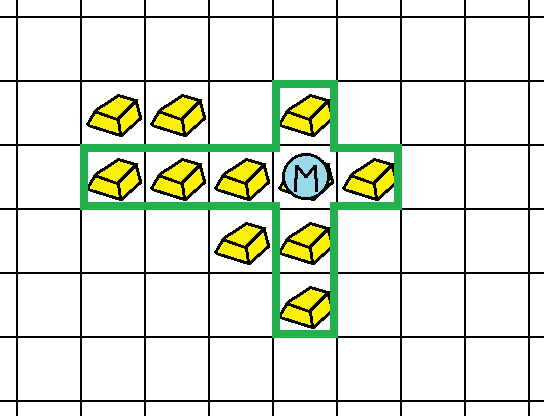 高橋君はすべての装置を順番を決めて作動させるつもりである。作動の順番によっては、最終的に得られる金塊の個数が変化するかもしれない。金塊が大好きな高橋君は、最終的に得られる金塊の個数をできるだけ多くしようと考えている。 あなたは高橋くんの代わりに、最大値を計算するプログラムを作成してほしい。

入力は以下の形式で標準入力から与えられる。 > $ W $ $ H $ $ N $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ : $ X_N $ $ Y_N $ - $ 1 $ 行目には、金塊の個数と配置に関する $ 2 $ つの整数 $ W\ (1\ ≦\ W\ ≦\ 10^6) $ と $ H\ (1\ ≦\ H\ ≦\ 10^6) $ が空白区切りで与えられる。 - $ 2 $ 行目には、金塊回収装置の個数を表す整数 $ N\ (1\ ≦\ N\ ≦\ 30) $ が与えられる。 - $ 3 $ 行目から $ N $ 行のうち $ i\ (1\ ≦\ i\ ≦\ N) $ 行目には、$ i $ 番目の装置があるマスに関する $ 2 $ つの整数 $ X_i\ (1\ ≦\ X_i\ ≦\ W) $ と $ Y_i\ (1\ ≦\ Y_i\ ≦\ H) $ が空白区切りで与えられる。これは、$ i $ 番目の装置がマス ($ X_i $ , $ Y_i $) にあることを表す。 また、この入力では、さらに以下の条件も満たされる。 - 任意の $ 2 $ つの整数 $ i,j\ (1\ ≦\ i\ について、X_i\ ≠\ X_j $ かつ $ Y_i\ ≠\ Y_j $ である。

回収可能な金塊の個数の最大値を出力せよ。出力の末尾にも改行を入れること。

### 部分点 この問題には部分点が設定されている。 - $ N\ ≦\ 8 $ , $ W\ ≦\ 80 $ , $ H\ ≦\ 80 $ を満たすデータセット $ 1 $ に正解した場合は、$ 80 $ 点が与えられる。 - $ W\ ≦\ 80 $ , $ H\ ≦\ 80 $ を満たすデータセット $ 2 $ に正解した場合は、さらに $ 19 $ 点が与えられ、合計で $ 99 $ 点が得られる。 - 追加制約のないデータセット $ 3 $ に正解した場合は、さらに $ 1 $ 点が与えられ、合計で $ 100 $ 点が得られる。 ### Sample Explanation 1 入力例 $ 1 $ において、初期状態は以下のようになっています。 !\[\](http://abc008.contest.atcoder.jp/img/abc/008/4-2.png)以下に示すように、$ 1 $ 番目、$ 2 $ 番目、$ 3 $ 番目の装置という順番で実行することにより、$ 19 $ 個の金塊を回収できます。 !\[\](http://abc008.contest.atcoder.jp/img/abc/008/4-3.png) ### Sample Explanation 2 うまく稼働させればすべての金塊を回収することができます。