AT_abc008_4 [ABC008D] 金塊ゲーム

高桥君正在玩一个基于无限二维网格的游戏。网格坐标系以 $(0, 0)$ 为原点，向东为 $x$ 轴正方向，向北为 $y$ 轴正方向。坐标为 $(x, y)$ 的格子表示从原点向东移动 $x$ 格（若 $x$ 为负则向西移动 $-x$ 格），向北移动 $y$ 格（若 $y$ 为负则向南移动 $-y$ 格）的位置。 网格中存在 $W \times H$ 个金块，分布在所有满足 $1 \leq p \leq W$ 且 $1 \leq q \leq H$ 的格子 $(p, q)$ 上。其中有恰好 $N$ 个格子设有金块回收装置（编号 $1$ 至 $N$）。装置满足以下条件： - 任意两个装置所在的格子 $(a, b)$ 和 $(c, d)$ 都满足 $a \neq c$ 且 $b \neq d$ - 每个装置所在的格子互不相同 当装置启动时，首先回收所在格子的金块，然后向东南西北四个方向延伸机械臂进行扩展回收。机械臂的延伸需满足以下规则： - **东向**：选择整数 $p > x+1$，使得区间 $(x+1, y)$ 到 $(p-1, y)$ 的格子均有金块，且 $(p, y)$ 无金块。回收该区间所有金块。 - **西向**：选择整数 $p < x-1$，使得区间 $(p+1, y)$ 到 $(x-1, y)$ 的格子均有金块，且 $(p, y)$ 无金块。回收该区间所有金块。 - **南向**：选择整数 $q < y-1$，使得区间 $(x, q+1)$ 到 $(x, y-1)$ 的格子均有金块，且 $(x, q)$ 无金块。回收该区间所有金块。 - **北向**：选择整数 $q > y+1$，使得区间 $(x, y+1)$ 到 $(x, q-1)$ 的格子均有金块，且 $(x, q)$ 无金块。回收该区间所有金块。 对于每个方向，若不存在满足条件的 $p$ 或 $q$，则无法在该方向延伸机械臂。此外，若某个方向存在可回收的金块，则必须执行回收操作。下图展示了满足条件的回收示例（图中以 `M` 表示装置，粗框表示可回收范围）。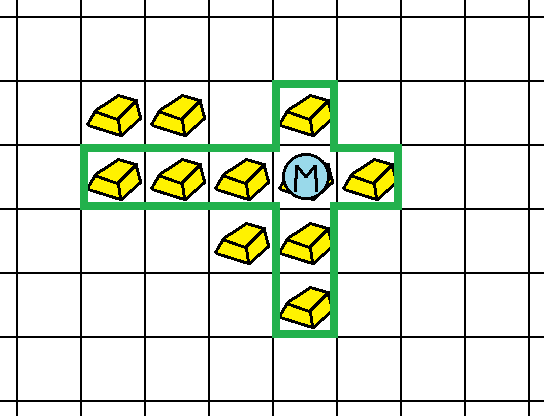  高桥君需要决定所有装置的启动顺序，不同的顺序可能导致最终回收数量不同。由于高桥君希望最大化金块回收量，请编写程序计算可能获得的最大金块数量。

输入通过标准输入给出： > $W$ $H$ > $N$ > $X_1$ $Y_1$ > $X_2$ $Y_2$ > ... > $X_N$ $Y_N$ - 第 1 行：两个整数 $W$ ($1 \leq W \leq 10^6$) 和 $H$ ($1 \leq H \leq 10^6$) - 第 2 行：整数 $N$ ($1 \leq N \leq 30$) - 后续 $N$ 行：每行两个整数 $X_i$ ($1 \leq X_i \leq W$) 和 $Y_i$ ($1 \leq Y_i \leq H$)，表示第 $i$ 个装置的位置 保证所有装置的位置满足 $X_i \neq X_j$ 且 $Y_i \neq Y_j$（$i \neq j$）

输出可回收金块的最大数量（末尾换行）

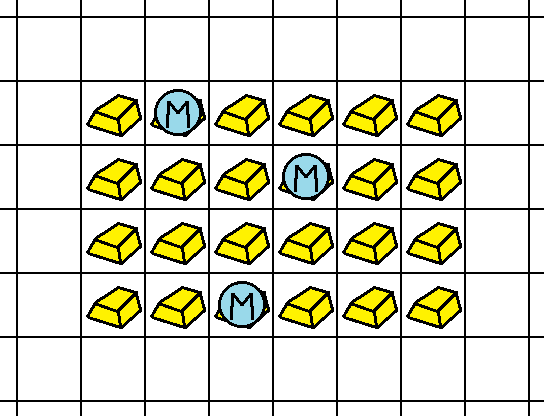
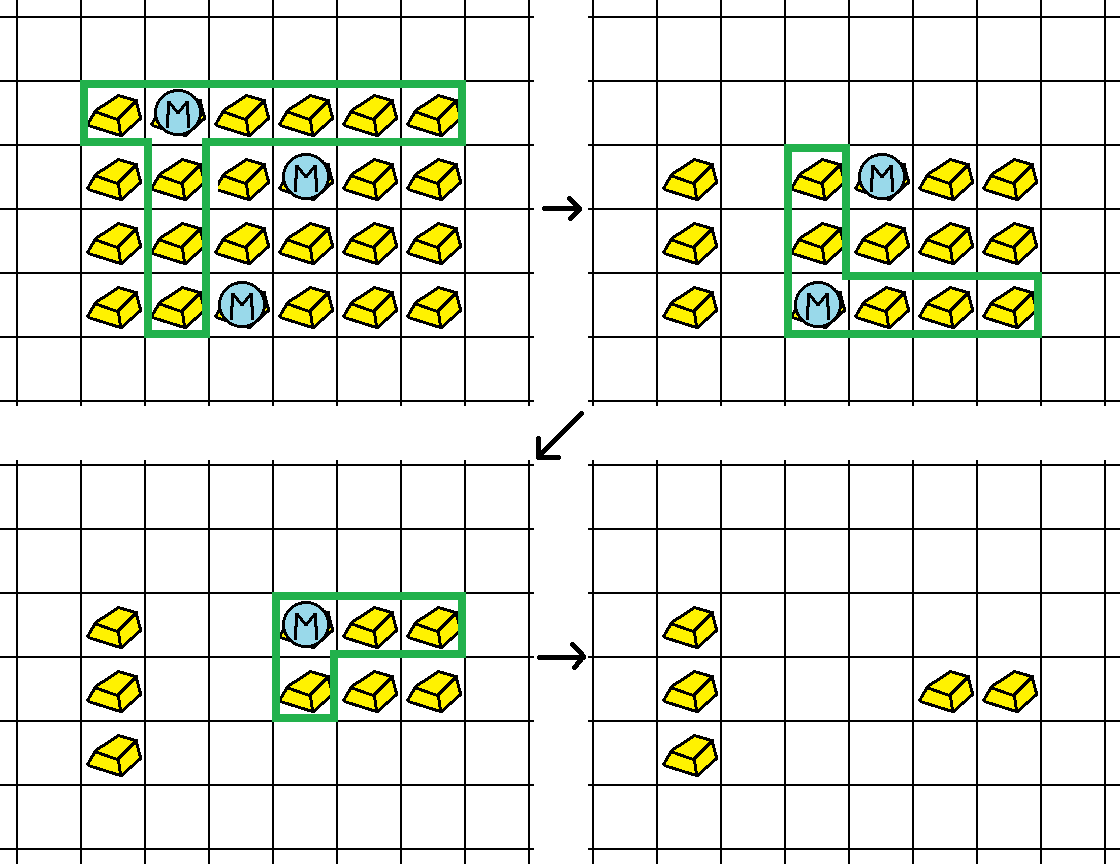
### 部分分 - 数据集 1 ($N \leq 8$, $W,H \leq 80$)：80 分 - 数据集 2 ($W,H \leq 80$)：合计 99 分 - 数据集 3 (无限制)：合计 100 分 ### 样例解释 1 输入样例 1 的初始状态如下图所示（图片链接保留）：  按照 1 号、2 号、3 号装置的顺序启动，可以回收 19 个金块，操作过程如下图所示：  ### 样例解释 2 存在可回收全部金块的启动顺序 翻译由 DeepSeek R1 完成