AT_abc013_4 [ABC013D] 阿弥陀

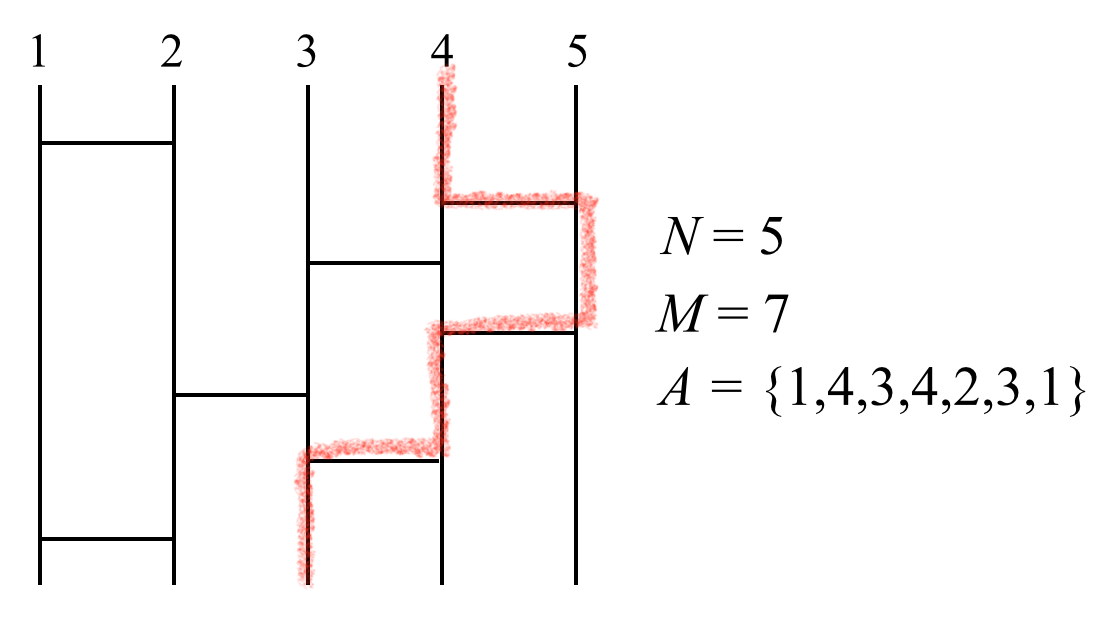
你知道从古至今传承下来的日本传统抽签方法——鬼脚图（日语：阿弥陀籤/あみだくじ）吗？ 进行鬼脚图时，首先画出 $N$ 条平行的竖线。接着，在这些竖线之间画 $M$ 条横线。每条横线必须连接相邻的两条竖线，且不能有两条或更多的横线在完全相同的高度上。假设从上往下数的第 $i$ 条横线连接了从左往右数的第 $A_i$ ($1\le A_i < N$) 条竖线和第 $A_i + 1$ 条竖线。 以下是 $N = 5,M = 7,A = \{1,4,3,4,2,3,1\}$ 情况下的鬼脚图示例。抽签时，从某条竖线的顶部出发，沿着线向下走。当遇到横线时，必须转弯，且不能回头向上。例如，在这个鬼脚图中，从左往右数第 $4$ 条竖线顶部开始，最终会到达左边数第 $3$ 条竖线的底部。  以上是普通的鬼脚图。然而，在“大数据”这一术语流行的当下，鬼脚图若想在未来继续存在下去，也需要“大”起来，以迎战“大数据”。 因此，我们考虑通过将多个鬼脚图**纵向连接 $D$ 次**，构造一个巨大的鬼脚图。例如，将上面提到的鬼脚图纵向连接 $2$ 次，可以得到如下示例。在这种情况下，从左边数第 $4$ 条竖线顶部开始抽签，最终会到达左边数第 $5$ 条竖线的底部。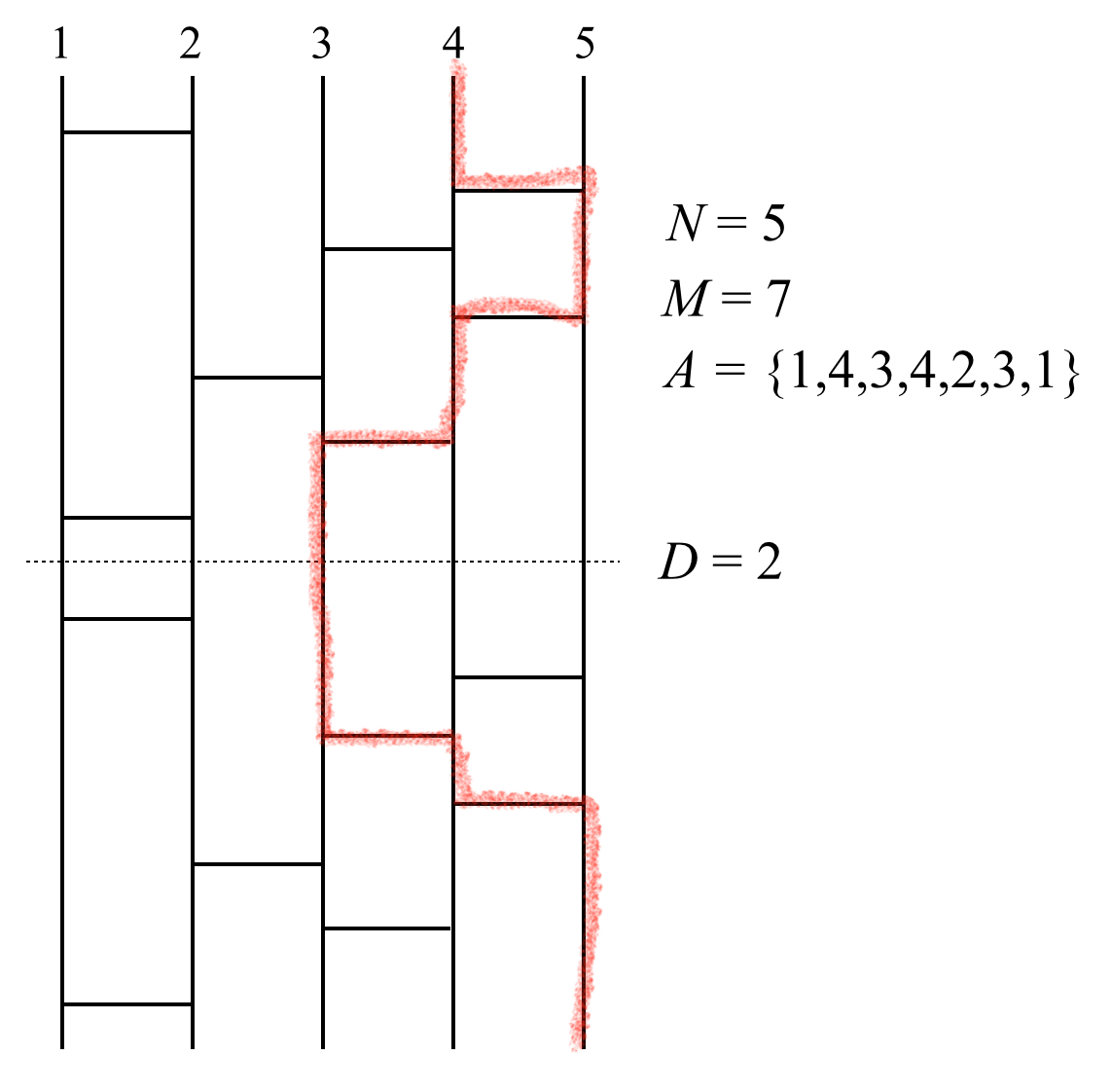  虽然我们构造了如此巨大的鬼脚图，但如果无法高效计算抽签的结果，这个巨大的鬼脚图也不过是徒有其表的涂鸦。因此，请编写一个程序，对于满足 $1\le k\le N$ 的每个整数 $k$，计算在巨大鬼脚图中，从左边数第 $k$ 条竖线顶部开始抽签，最终会到达左边数第几条竖线底部。

输入以以下格式通过标准输入提供： > $N$ $M$ $D$ $A_1$ $A_2$ $\cdots$ $A_M$ - 第 1 行包含 $3$ 个整数，表示初始鬼脚图的竖线数量 $N$（$2\le N\le 10^5$）、横线数量 $M$（$0\le M\le 2 \times 10^5$）、以及将初始鬼脚图纵向连接的次数 $D$（$1\le D\le 10^9$）。 - 第 2 行包含 $M$ 个整数 $A_1, A_2, \cdots, A_M$（$1\le A_i < N$），表示每条横线的连接信息。

输出 $N$ 行，第 $k$ 行输出一个整数，表示在巨大鬼脚图中，从左边数第 $k$ 条竖线顶部开始抽签，最终会到达左边数第几条竖线底部。 输出的末尾需包含换行符。 ### 部分分 测试样例分为 4 组，分别有如下限制条件及分数： 1. 第一组：$D = 1$，全部正确可得 $10$ 分。 2. 第二组：$N\le 1000$ 且 $D\le 1000$，全部正确可得 $20$ 分。 3. 第三组：$N\le 8$，全部正确可得 $20$ 分。 4. 第四组：无额外限制条件，全部正确可得 $50$ 分。 题面译自 [D - 阿弥陀](https://atcoder.jp/contests/abc013/tasks/abc013_4)。翻译来自于 [ChatGPT](https://chatgpt.com) 并进行人工校对，若有误请联系 [rui_er](https://www.luogu.com.cn/user/122461)。

### 部分点 この問題のテストケースは $ 4 $ つのグループに分けられており、それぞれに配点が決まっている。 - $ 1 $ つめのグループにおいて、テストケースは $ D\ =\ 1 $ を満たす。このグループのテストケース全てに正解すると $ 10 $ 点が与えられる。 - $ 2 $ つめのグループにおいて、テストケースは $ N\,≦\,1,000 $ および $ D\,≦\,1,000 $ を満たす。このグループのテストケース全てに正解すると $ 20 $ 点が与えられる。 - $ 3 $ つめのグループにおいて、テストケースは $ N\,≦\,8 $ を満たす。このグループのテストケース全てに正解すると $ 20 $ 点が与えられる。 - $ 4 $ つめのグループにおいてはテストケースに追加の制限はない。このグループのテストケース全てに正解すると $ 50 $ 点が与えられる。 ### Sample Explanation 1 この入出力例は問題文中の最初の図で示されたあみだくじに対応している。 ### Sample Explanation 2 この入出力例は問題文中の $ 2 $ 番目の図で示されたあみだくじに対応している。このケースは $ 1 $ つめのテストグループの制約を満たさないことに注意せよ。 ### Sample Explanation 3 このケースは $ 1 $ つめおよび $ 3 $ つめのテストグループの制約を満たさないことに注意せよ。