AT_abc184_c [ABC184C] Super Ryuma

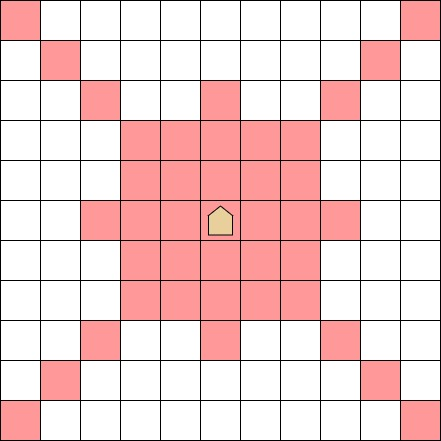
在一个无限扩展的二维网格上，棋子“超竜馬”被放置在格子 $(r_1,\ c_1)$ 上。 该棋子每一步可以进行如下移动。  更准确地说，当超竜馬在格子 $(a,\ b)$ 时，可以移动到满足以下任一条件的格子 $(c,\ d)$： - $a + b = c + d$ - $a - b = c - d$ - $|a - c| + |b - d| \le 3$ 请你求出将超竜馬从 $(r_1,\ c_1)$ 移动到 $(r_2,\ c_2)$ 所需的最小步数。

输入以如下格式从标准输入给出。 > $r_1$ $c_1$ $r_2$ $c_2$

输出将超竜馬从 $(r_1,\ c_1)$ 移动到 $(r_2,\ c_2)$ 所需的最小步数。

## 限制条件 - 输入均为整数 - $1 \le r_1, c_1, r_2, c_2 \le 10^9$ ## 样例解释 1 例如，若按 $(1, 1) \rightarrow (5, 5) \rightarrow (5, 6)$ 移动，则需要 $2$ 步。 ## 样例解释 2 例如，若按 $(1, 1) \rightarrow (100001, 100001) \rightarrow (1, 200001)$ 移动，则需要 $2$ 步。 ## 样例解释 3 例如，若按 $(2, 3) \rightarrow (3, 3) \rightarrow (-247, 253) \rightarrow (998244353, 998244853)$ 移动，则需要 $3$ 步。 由 ChatGPT 4.1 翻译