AT_abc184_c [ABC184C] Super Ryuma

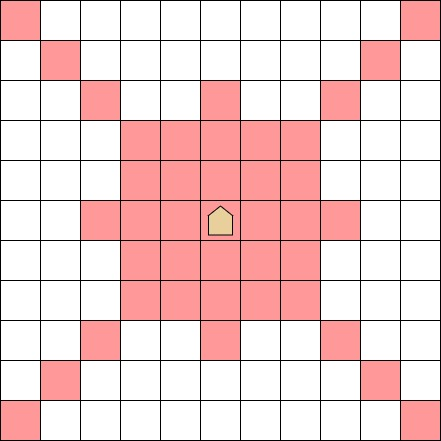
[problemUrl]: https://atcoder.jp/contests/abc184/tasks/abc184_c 無限に広がる $ 2 $ 次元グリッドがあり、マス $ (r_1,\ c_1) $ に駒「超竜馬」が置かれています。 この駒は、 $ 1 $ 手で次のような動きができます。  より正確には、超竜馬がマス $ (a,\ b) $ にあるとき、以下のいずれかの条件を満たすマス $ (c,\ d) $ に動かすことができます。 - $ a\ +\ b\ =\ c\ +\ d $ - $ a\ -\ b\ =\ c\ -\ d $ - $ |a\ -\ c|\ +\ |b\ -\ d|\ \le\ 3 $ 超竜馬を $ (r_1,\ c_1) $ から $ (r_2,\ c_2) $ に動かすのに必要な最小手数を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ r_1 $ $ c_1 $ $ r_2 $ $ c_2 $

超竜馬を $ (r_1,\ c_1) $ から $ (r_2,\ c_2) $ に動かすのに必要な最小手数を出力せよ。

### 制約 - 入力は全て整数 - $ 1\ \le\ r_1,\ c_1,\ r_2,\ c_2\ \le\ 10^9 $ ### Sample Explanation 1 例えば、 $ (1,\ 1)\ \rightarrow\ (5,\ 5)\ \rightarrow\ (5,\ 6) $ と動かすと $ 2 $ 手になります。 ### Sample Explanation 2 例えば、 $ (1,\ 1)\ \rightarrow\ (100001,\ 100001)\ \rightarrow\ (1,\ 200001) $ と動かすと $ 2 $ 手になります。 ### Sample Explanation 3 例えば、 $ (2,\ 3)\ \rightarrow\ (3,\ 3)\ \rightarrow\ (-247,\ 253)\ \rightarrow\ (998244353,\ 998244853) $ と動かすと $ 3 $ 手になります。