AT_abc239_c [ABC239C] Knight Fork

[problemUrl]: https://atcoder.jp/contests/abc239/tasks/abc239_c $ xy $ 座標平面上の $ 2 $ つの格子点 $ (x_1,\ y_1),\ (x_2,\ y_2) $ からの距離がともに $ \sqrt{5} $ である格子点は存在しますか？

入力は以下の形式で標準入力から与えられる。 > $ x_1 $ $ y_1 $ $ x_2 $ $ y_2 $

条件を満たす格子点が存在する場合は `Yes` を、存在しない場合は `No` を出力せよ。

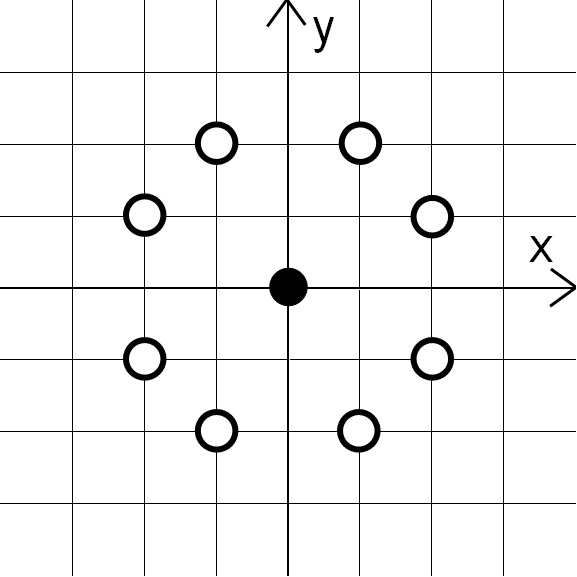
### 注記 $ xy $ 座標平面上にある点のうち、$ x $ 座標と $ y $ 座標がともに整数である点を格子点と呼びます。 また、$ xy $ 平面上の $ 2 $ 点 $ (a,\ b),\ (c,\ d) $ の距離をユークリッド距離 $ \sqrt{(a\ -\ c)^2\ +\ (b-d)^2} $ として定義します。 参考として、$ xy $ 平面の $ (0,\ 0) $ の上に黒丸を、$ (0,\ 0) $ からの距離が $ \sqrt{5} $ となる格子点の上に白丸を書いた図は以下のようになります。($ x,y $ いずれかが整数となる部分に目盛り線を引いています。)  ### 制約 - $ -10^9\ \leq\ x_1\ \leq\ 10^9 $ - $ -10^9\ \leq\ y_1\ \leq\ 10^9 $ - $ -10^9\ \leq\ x_2\ \leq\ 10^9 $ - $ -10^9\ \leq\ y_2\ \leq\ 10^9 $ - $ (x_1,\ y_1)\ \neq\ (x_2,\ y_2) $ - 入力はすべて整数である。 ### Sample Explanation 1 \- 点 $ (2,1) $ と $ (x_1,\ y_1) $ の距離は $ \sqrt{(0-2)^2\ +\ (0-1)^2}\ =\ \sqrt{5} $ - 点 $ (2,1) $ と $ (x_2,\ y_2) $ の距離は $ \sqrt{(3-2)^2\ +\ (3-1)^2}\ =\ \sqrt{5} $ - 点 $ (2,\ 1) $ は格子点 なので点 $ (2,\ 1) $ は条件を満たします。よって `Yes` を出力します。 なお、点 $ (1,\ 2) $ も条件を満たすことが同様にして確認できます。 ### Sample Explanation 2 条件を満たす格子点は存在しません。よって `No` を出力します。 ### Sample Explanation 3 点 $ (10^9\ +\ 1,\ 10^9\ -\ 2) $ および点 $ (10^9\ -\ 2,\ 10^9\ +\ 1) $が条件を満たします。