AT_abc239_c [ABC239C] Knight Fork

在 $xy$ 坐标平面上，是否存在一个格点，使得它到两个给定格点 $(x_1, y_1)$ 和 $(x_2, y_2)$ 的距离均为 $\sqrt{5}$？

输入从标准输入中给出，格式如下： > $x_1$ $y_1$ $x_2$ $y_2$

如果存在满足条件的格点，输出 `Yes`；否则输出 `No`。

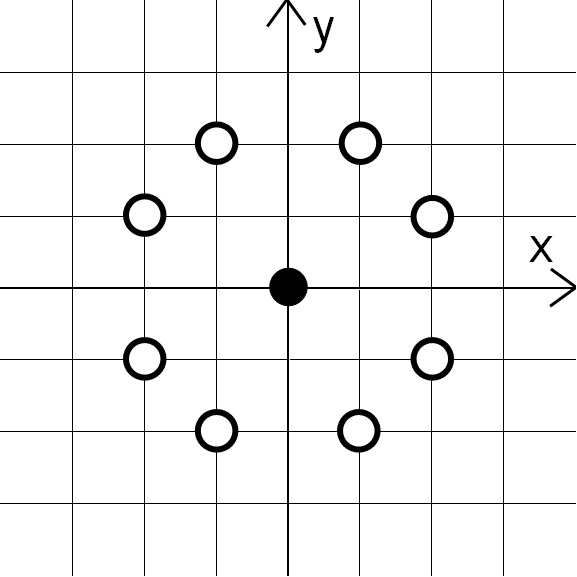
## 注释 在 $xy$ 坐标平面上，$x$ 坐标和 $y$ 坐标均为整数的点称为格点。 此外，$xy$ 平面上两点 $(a, b)$ 和 $(c, d)$ 之间的距离定义为欧几里得距离 $\sqrt{(a-c)^2 + (b-d)^2}$。 作为参考，下图中，$xy$ 平面上的 $(0, 0)$ 处为黑点，距离 $(0, 0)$ 为 $\sqrt{5}$ 的格点处为白点。（图中在 $x$ 或 $y$ 为整数的位置画有刻度线。）  ## 数据范围 - $-10^9 \leq x_1 \leq 10^9$ - $-10^9 \leq y_1 \leq 10^9$ - $-10^9 \leq x_2 \leq 10^9$ - $-10^9 \leq y_2 \leq 10^9$ - $(x_1, y_1) \neq (x_2, y_2)$ - 输入均为整数。 ## 样例解释 1 - 点 $(2, 1)$ 到 $(0, 0)$ 的距离为 $\sqrt{(0-2)^2 + (0-1)^2} = \sqrt{5}$。 - 点 $(2, 1)$ 到 $(3, 3)$ 的距离为 $\sqrt{(3-2)^2 + (3-1)^2} = \sqrt{5}$。 - 点 $(2, 1)$ 是格点，因此 $(2, 1)$ 满足条件，输出 `Yes`。同理，点 $(1, 2)$ 也满足条件。 ## 样例解释 2 不存在满足条件的格点，因此输出 `No`。 ## 样例解释 3 点 $(10^9 + 1, 10^9 - 2)$ 以及点 $(10^9 - 2, 10^9 + 1)$ 均满足条件。 由 ChatGPT 4.1 翻译