AT_abc243_c [ABC243C] Collision 2

[problemUrl]: https://atcoder.jp/contests/abc243/tasks/abc243_c $ xy $ 座標平面上に $ N $ 人の人がいます。人 $ i $ は $ (X_i,\ Y_i) $ にいます。すべての人は異なる地点にいます。 `L`, `R` からなる長さ $ N $ の文字列 $ S $ があります。 人 $ i $ は $ S_i\ = $ `R` ならば右向きに、$ S_i\ = $ `L` ならば左向きに、一斉に同じ速度で歩き始めます。ここで、右は $ x $ 軸の正の向き、左は $ x $ 軸の負の向きです。 たとえば $ (X_1,\ Y_1)\ =\ (2,\ 3),\ (X_2,\ Y_2)\ =\ (1,\ 1),\ (X_3,\ Y_3)\ =(4,\ 1),\ S\ = $ `RRL` の場合は次の図のように動きます。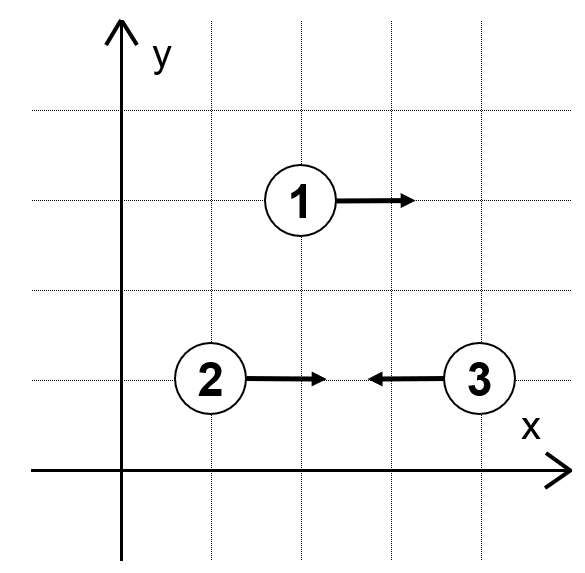  反対の向きに歩いている人同士が同じ地点に来ることを「衝突」と呼びます。すべての人が歩き続けたとき、衝突は発生しますか？

入力は以下の形式で標準入力から与えられる。 > $ N $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ $ \vdots $ $ X_N $ $ Y_N $ $ S $

衝突が発生するならば `Yes` を、発生しないならば `No` を出力せよ。

### 制約 - $ 2\ \leq\ N\ \leq\ 2\ \times\ 10^5 $ - $ 0\ \leq\ X_i\ \leq\ 10^9 $ - $ 0\ \leq\ Y_i\ \leq\ 10^9 $ - $ i\ \neq\ j $ ならば $ (X_i,\ Y_i)\ \neq\ (X_j,\ Y_j) $ である。 - $ X_i,\ Y_i $ はすべて整数である。 - $ S $ は `L` および `R` からなる長さ $ N $ の文字列である。 ### Sample Explanation 1 この入力は問題文にある例と同じケースです。 すべての人が歩き続けると人 $ 2 $ と人 $ 3 $ が衝突します。よって `Yes` を出力します。 ### Sample Explanation 2 人 $ 1 $ と人 $ 2 $ は同じ向きに歩いているので衝突することはありません。