AT_abc248_f [ABC248F] Keep Connect

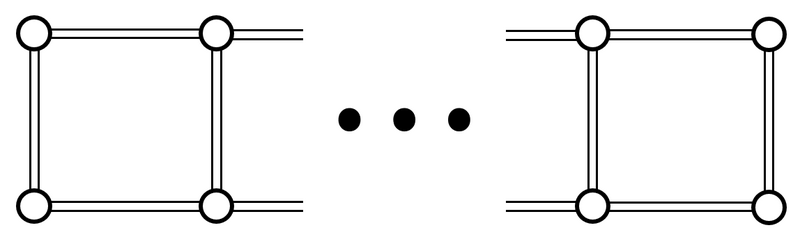
给定一个整数 $N \geq 2$ 和一个素数 $P$。 考虑如下图所示的一个有 $2N$ 个顶点、$(3N-2)$ 条边的图 $G$。  更具体地说，顶点依次编号为 $1, 2, \ldots, 2N$，边依次编号为 $1, 2, \ldots, 3N-2$，每条边连接的顶点如下： - 对于 $1 \leq i \leq N-1$，边 $i$ 连接顶点 $i$ 和顶点 $i+1$。 - 对于 $1 \leq i \leq N-1$，边 $(N-1+i)$ 连接顶点 $N+i$ 和顶点 $N+i+1$。 - 对于 $1 \leq i \leq N$，边 $(2N-2+i)$ 连接顶点 $i$ 和顶点 $N+i$。 对于 $i=1,2,\ldots,N-1$，请解决以下问题： > 从 $G$ 的 $3N-2$ 条边中恰好去除 $i$ 条边，使得去除后的图仍然连通。请计算这样的方案数，并对 $P$ 取模。

输入为一行，包含两个整数 $N$ 和 $P$。

输出 $N-1$ 个整数，空格分隔。第 $k$ 个整数表示 $i=k$ 时的答案。

## 限制条件 - $2 \leq N \leq 3000$ - $9 \times 10^8 \leq P \leq 10^9$ - $N$ 是整数。 - $P$ 是素数。 ## 样例解释 1 以 $N=3$ 为例，恰好去除 $1$ 条边且去除后图仍然连通的方案有如下 $7$ 种。  恰好去除 $2$ 条边且去除后图仍然连通的方案有如下 $15$ 种。  因此，对 $P=998244353$ 取模后，依次输出 $7$ 和 $15$。 ## 样例解释 2 请注意，输出时需要对 $P$ 取模。 由 ChatGPT 4.1 翻译