AT_abc248_f [ABC248F] Keep Connect

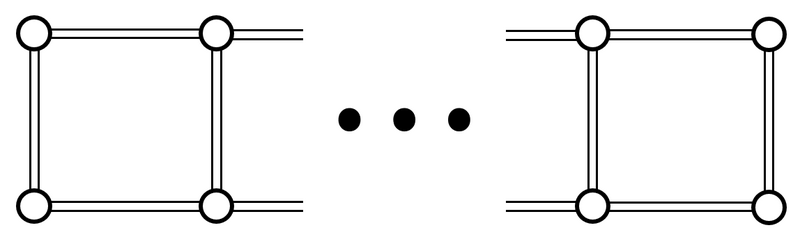
[problemUrl]: https://atcoder.jp/contests/abc248/tasks/abc248_f $ 2 $ 以上の整数 $ N $ および素数 $ P $ が与えられます。 下図のような $ 2N $ 頂点 $ (3N-2) $ 辺のグラフ $ G $ を考えます。  より具体的には、頂点を順に頂点 $ 1 $, 頂点 $ 2 $, $ \ldots $, 頂点 $ 2N $、 辺を順に辺 $ 1 $, 辺 $ 2 $, $ \ldots $, 辺 $ (3N-2) $ とすると、各辺は次のように頂点を結んでいます。 - $ 1\leq\ i\leq\ N-1 $ について、辺 $ i $ は頂点 $ i $ と頂点 $ i+1 $ を結んでいる。 - $ 1\leq\ i\leq\ N-1 $ について、辺 $ (N-1+i) $ は頂点 $ N+i $ と頂点 $ N+i+1 $ を結んでいる。 - $ 1\leq\ i\leq\ N $ について、辺 $ (2N-2+i) $ は頂点 $ i $ と頂点 $ N+i $ を結んでいる。 $ i=1,2,\ldots\ ,N-1 $ について、次の問題を解いてください。 > $ G $ の $ 3N-2 $ 本の辺からちょうど $ i $ 本の辺を取り除く方法であって、辺を取り除いた後のグラフも連結であるようなものの個数を $ P $ で割ったあまりを求めよ。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ P $

$ N-1 $ 個の整数を空白区切りで出力せよ。 ただし、$ k $ 番目の整数は $ i=k $ に対する答えである。

### 制約 - $ 2\ \leq\ N\ \leq\ 3000 $ - $ 9\times\ 10^8\ \leq\ P\ \leq\ 10^9 $ - $ N $ は整数である。 - $ P $ は素数である。 ### Sample Explanation 1 $ N=3 $ の場合について、取り除いた後のグラフも連結となるように、ちょうど $ 1 $ 本の辺を取り除く方法は次の $ 7 $ 通りです。 !\[\](https://img.atcoder.jp/abc248/57f65600b77ee654900cff4ea6e40872.png) 取り除いた後のグラフも連結となるように、ちょうど $ 2 $ 本の辺を取り除く方法は次の $ 15 $ 通りです。 !\[\](https://img.atcoder.jp/abc248/3a7d6523a1252886e9a33204a32e45f5.png) よって、これらを $ P=998244353 $ で割ったあまりである $ 7 $, $ 15 $ をこの順に出力します。 ### Sample Explanation 2 $ P $ で割ったあまりを出力することに注意してください。