AT_abc265_h [ABC265Ex] No-capture Lance Game

[problemUrl]: https://atcoder.jp/contests/abc265/tasks/abc265_h 縦横 $ H\ \times\ W $ マスの将棋盤と $ 2\ \times\ H $ 枚の将棋の香車の駒があります。これらを用いて次のようなゲームを考えます。 ゲームは先手と後手の二人によって行われ、以下に示す手順で進行します。 - 初期状態では、先手の香車と後手の香車がすべての行に $ 1 $ 枚ずつ配置されている。 - 先手から始めて先手と後手で交互に自分の駒を動かしていく。ただし**相手の駒を取る(盤面から取り除く)ことはできない**。 - 先に全ての自分の駒を動かせなくなった方が負けとなり、そうでない方は勝ちになる。 香車の動かせる場所は次のように定めます。ここで $ (i,j) $ を上から $ i $ 行目、左から $ j $ 列目のマスとします。 - $ k\ \lt\ j $ かつ $ (i,k),(i,k+1),\dots,(i,j-1) $ に双方の駒が存在しないとき、$ (i,j) $ にある先手の香車を $ (i,k) $ に動かすことが出来る。 - $ k\ \gt\ j $ かつ $ (i,j+1),(i,j+2),\dots,(i,k) $ に双方の駒が存在しないとき、$ (i,j) $ にある後手の香車を $ (i,k) $ に動かすことが出来る。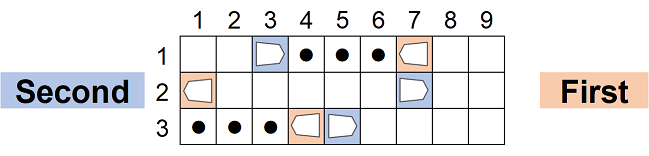 例えば下の図では、$ 3\times\ 9 $ の将棋盤の $ (1,7),(2,1),(3,4) $ に先手の香車が、$ (1,3),(2,7),(3,5) $ に後手の香車が置かれています。 $ (1,7) $ の先手の香車は $ (1,4),(1,5),(1,6) $ のいずれかのマスへ、$ (3,4) $ の先手の香車は $ (3,1),(3,2),(3,3) $ のいずれかのマスへ動かすことができます。$ (2,1) $ の先手の香車は動かすことができません。 将棋を知っている人は、通常の将棋に存在する「取る」「成る」などのルールは適用されないことに注意してください。  今、将棋盤の上には何もありません。先手の香車と後手の香車を、双方の香車が同じマスに置かれないように各行に $ 1 $ 枚ずつ置く方法は $ \left\lbrace\ W(W-1)\right\rbrace^H $ 通りあります。そのうち次の条件を満たす配置は何通りありますか？答えを $ 998244353 $ で割ったあまりを求めてください。 - その配置を初期配置としてゲームを開始して双方が最適にゲームを進めた時に先手が勝つことができる。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $

答えを出力せよ。

### 制約 - $ 1\ \leq\ H\ \leq\ 8000 $ - $ 2\ \leq\ W\ \leq\ 30 $ - $ H,\ W $ は整数 ### Sample Explanation 1 先手が勝てる配置は次の $ 2 $ 通りです。 - 先手の香車を $ (1,\ 3) $ に、後手の香車を $ (1,\ 1) $ に配置した場合。 - 先手の香車を $ (1,\ 2) $ に、後手の香車を $ (1,\ 3) $ に配置した場合。