AT_abc265_h [ABC265Ex] No-capture Lance Game

有一个 $H \times W$ 的将棋棋盘，以及 $2 \times H$ 枚将棋中的香车棋子。我们用这些棋子来进行如下的游戏。 游戏由先手和后手两人进行，按照以下步骤进行。 - 初始状态下，先手和后手的香车分别在每一行各放置一枚。 - 从先手开始，先手和后手轮流移动自己的棋子。**不能吃掉（从棋盘上移除）对方的棋子**。 - 最先无法移动自己所有棋子的一方判负，另一方获胜。 香车的可移动规则如下。设 $(i, j)$ 表示从上到下第 $i$ 行，从左到右第 $j$ 列的格子。 - 若 $k < j$ 且 $(i, k), (i, k+1), \dots, (i, j-1)$ 上都没有任何棋子，则可以将位于 $(i, j)$ 的先手香车移动到 $(i, k)$。 - 若 $k > j$ 且 $(i, j+1), (i, j+2), \dots, (i, k)$ 上都没有任何棋子，则可以将位于 $(i, j)$ 的后手香车移动到 $(i, k)$。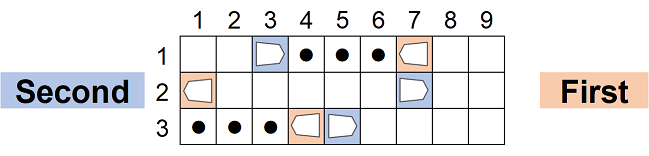 例如，下图为 $3 \times 9$ 的棋盘，先手香车分别放在 $(1,7), (2,1), (3,4)$，后手香车分别放在 $(1,3), (2,7), (3,5)$。 $(1,7)$ 的先手香车可以移动到 $(1,4), (1,5), (1,6)$ 中的任意一个格子，$(3,4)$ 的先手香车可以移动到 $(3,1), (3,2), (3,3)$ 中的任意一个格子。$(2,1)$ 的先手香车无法移动。 了解将棋的人请注意，本题不适用通常将棋中的“吃子”“升变”等规则。  现在，棋盘上还没有任何棋子。将先手和后手的香车分别在每一行各放置一枚，且双方的香车不能放在同一个格子上的方案共有 $\left\lbrace W(W-1)\right\rbrace^H$ 种。在这些方案中，满足以下条件的方案有多少种？请输出答案对 $998244353$ 取模的结果。 - 以该方案为初始状态开始游戏，双方都采取最优策略时，先手能够获胜。

输入为一行，格式如下： > $H$ $W$

请输出答案。

## 限制条件 - $1 \leq H \leq 8000$ - $2 \leq W \leq 30$ - $H, W$ 为整数 ## 样例解释 1 先手能够获胜的方案有如下 $2$ 种： - 先手香车放在 $(1, 3)$，后手香车放在 $(1, 1)$。 - 先手香车放在 $(1, 2)$，后手香车放在 $(1, 3)$。 由 ChatGPT 4.1 翻译