AT_abc267_b [ABC267B] Split?

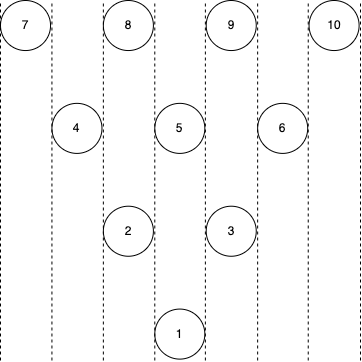
[problemUrl]: https://atcoder.jp/contests/abc267/tasks/abc267_b ボウリングのピンは $ 1 $ から $ 10 $ の番号が付けられており、上から見ると下図のように配置されます。  この図の二つの点線に挟まれた部分を**列**と呼ぶことにします。 例えば、ピン $ 1,\ 5 $ とピン $ 3,\ 9 $ はそれぞれ同じ列に存在します。 いくつかのピンが倒れた状態のうち、特殊なものは**スプリット**と呼ばれます。 ピンの配置がスプリットであるとは、以下の条件が全て成り立つことを言います。 - ピン $ 1 $ が倒れている。 - ある二つの異なる列であって、次の条件を満たすものが存在する。 - それぞれの列には、立っているピンが $ 1 $ 本以上存在する。 - それらの列の間に、ピンが全て倒れている列が存在する。 具体例は入出力例を参考にしてください。 さて、あるピンの配置が長さ $ 10 $ の文字列 $ S $ として与えられます。 $ i\ =\ 1,\ \dots,\ 10 $ について、ピン $ i $ が倒れているとき $ S $ の $ i $ 文字目は `0` であり、ピン $ i $ が立っているとき $ S $ の $ i $ 文字目は `1` です。 $ S $ で表されるピンの配置がスプリットかどうか判定してください。

入力は以下の形式で標準入力から与えられる。 > $ S $

$ S $ で表されるピンの配置がスプリットなら `Yes` を、そうでないなら `No` を出力せよ。

### 制約 - $ S $ は `0` と `1` からなる長さ $ 10 $ の文字列 ### Sample Explanation 1 倒れているピンを灰色で、立っているピンを白色で示すと下図のようになります。 !\[ex0\](https://img.atcoder.jp/abc267/ec8920ee4b39fac21b10c03e44fa45da.png) ピン $ 5 $ が立っている列とピン $ 6 $ が立っている列の間にはピン $ 3,\ 9 $ が置かれている列が存在しますが、ピン $ 3,\ 9 $ はいずれも倒れているので、この配置はスプリットです。 ### Sample Explanation 2 !\[ex1\](https://img.atcoder.jp/abc267/6ad2c3b72be7f1200386be1fb1eb276c.png) ### Sample Explanation 3 !\[ex2\](https://img.atcoder.jp/abc267/2d5b61ba048cf10007ce5b7a984c41a6.png) この配置はスプリットではありません。 ### Sample Explanation 4 !\[ex3\](https://img.atcoder.jp/abc267/d3aea8dae7928a938605b7a613bb642c.png) ピン $ 1 $ が倒れていないので、スプリットではありません。