AT_abc300_c [ABC300C] Cross

有一个高 $H$ 行、宽 $W$ 列的网格。我们称网格从上到下第 $i$ 行、从左到右第 $j$ 列的格子为 $(i, j)$。 每个格子上写有 `#` 或 `.`。记 $(i, j)$ 上写的字符为 $C[i][j]$。另外，如果整数 $i, j$ 不满足 $1 \leq i \leq H$ 或 $1 \leq j \leq W$，则定义 $C[i][j] = \texttt{.}$。 当正整数 $a, b, n$ 满足以下所有条件时，称 $4n+1$ 个格子 $(a, b)$ 以及 $(a+d, b+d), (a+d, b-d), (a-d, b+d), (a-d, b-d)$（$1 \leq d \leq n$）组成了**以 $(a, b)$ 为中心、大小为 $n$ 的“バツ印”**： - $C[a][b]$ 为 `#`。 - 对于所有满足 $1 \leq d \leq n$ 的整数 $d$，$C[a+d][b+d], C[a+d][b-d], C[a-d][b+d], C[a-d][b-d]$ 都为 `#`。 - $C[a+n+1][b+n+1], C[a+n+1][b-n-1], C[a-n-1][b+n+1], C[a-n-1][b-n-1]$ 中至少有一个为 `.`。 例如，下图中，存在以 $(2, 2)$ 为中心、大小为 $1$ 的“バツ印”，以及以 $(3, 7)$ 为中心、大小为 $2$ 的“バツ印”。  网格上有若干个“バツ印”。除了组成“バツ印”的格子外，没有其它格子上写有 `#`。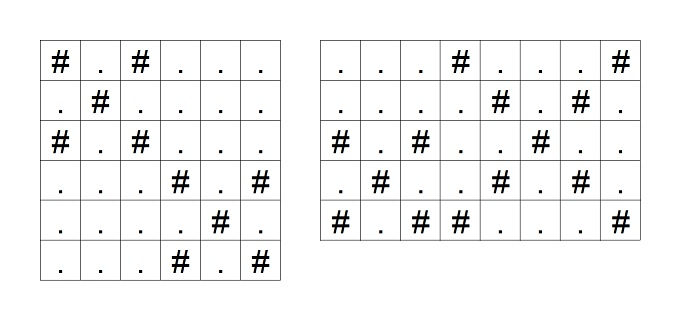 此外，不同“バツ印”所占据的格子不会在顶点处相交。下图是两个不同“バツ印”在顶点处相交的例子，**这样的网格不会作为输入给出**。例如左图中，$(3, 3)$ 和 $(4, 4)$ 在顶点处相交，违反了条件。  令 $N = \min(H, W)$。记大小为 $n$ 的“バツ印”个数为 $S_n$。请计算 $S_1, S_2, \dots, S_N$。

输入从标准输入读入，格式如下： > $H$ $W$ > $C[1][1]C[1][2]\dots C[1][W]$ > $C[2][1]C[2][2]\dots C[2][W]$ > $\vdots$ > $C[H][1]C[H][2]\dots C[H][W]$

请输出 $S_1, S_2, \dots, S_N$，用空格分隔。

## 限制条件 - $3 \leq H, W \leq 100$ - $C[i][j]$ 为 `#` 或 `.` - 不同“バツ印”所占据的格子不会在顶点处相交 - $H, W$ 为整数 ## 样例解释 1 如题目描述所示，存在以 $(2, 2)$ 为中心、大小为 $1$ 的“バツ印”，以及以 $(3, 7)$ 为中心、大小为 $2$ 的“バツ印”。 ## 样例解释 2 也有可能没有任何“バツ印”。 由 ChatGPT 4.1 翻译