AT_abc354_d [ABC354D] AtCoder Wallpaper

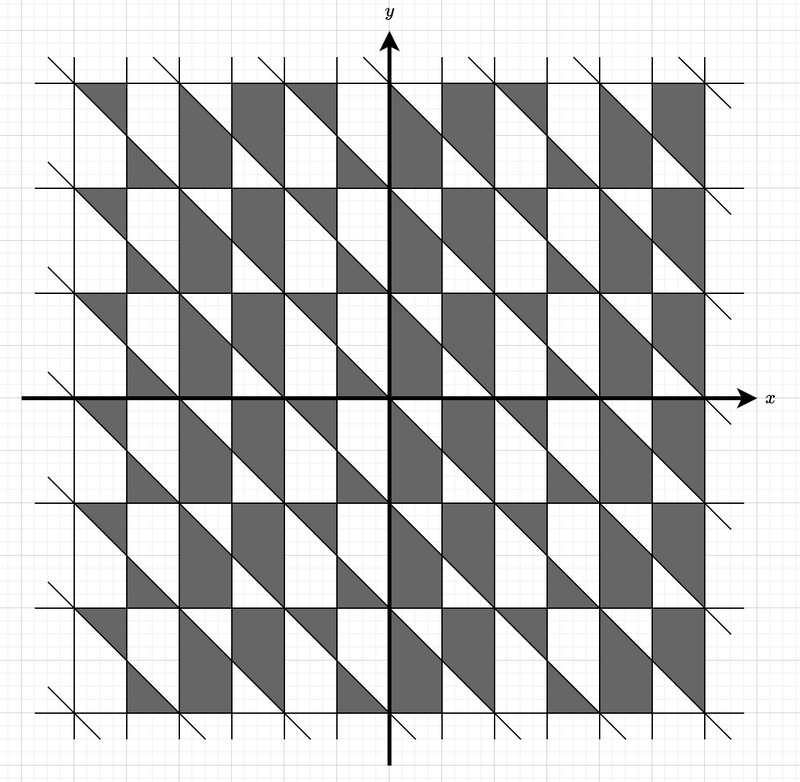
[problemUrl]: https://atcoder.jp/contests/abc354/tasks/abc354_d AtCoder 社の壁紙の模様を $ xy $ 平面上に表現すると、以下のようになります。 - 以下の $ 3 $ 種類の直線で領域が分割されている。 - $ x\ =\ n $ ($ n $ は整数) - $ y\ =\ n $ ($ n $ は偶数) - $ x\ +\ y\ =\ n $ ($ n $ は偶数) - 各領域は白もしくは黒で塗られている。いずれかの直線で隣接する $ 2 $ 領域は異なる色で塗られている。 - $ (0.5,\ 0.5) $ を含む領域は黒で塗られている。 下の図は、模様の一部を表したものです。  整数 $ A,\ B,\ C,\ D $ が与えられます。各辺が $ x,\ y $ 軸に平行で、左下の頂点が $ (A,\ B) $ にあり右上の頂点が $ (C,\ D) $ にあるような長方形を考えます。この長方形の内側に存在する黒で塗られた領域の面積を求め、それを $ 2 $ 倍したものを出力してください。 出力する値は整数になることが証明できます。

入力は以下の形式で標準入力から与えられる。 > $ A $ $ B $ $ C $ $ D $

答えを一行に出力せよ。

### 制約 - $ -10^9\ \leq\ A,\ B,\ C,\ D\ \leq\ 10^9 $ - $ A\