AT_abc354_d [ABC354D] AtCoder Wallpaper

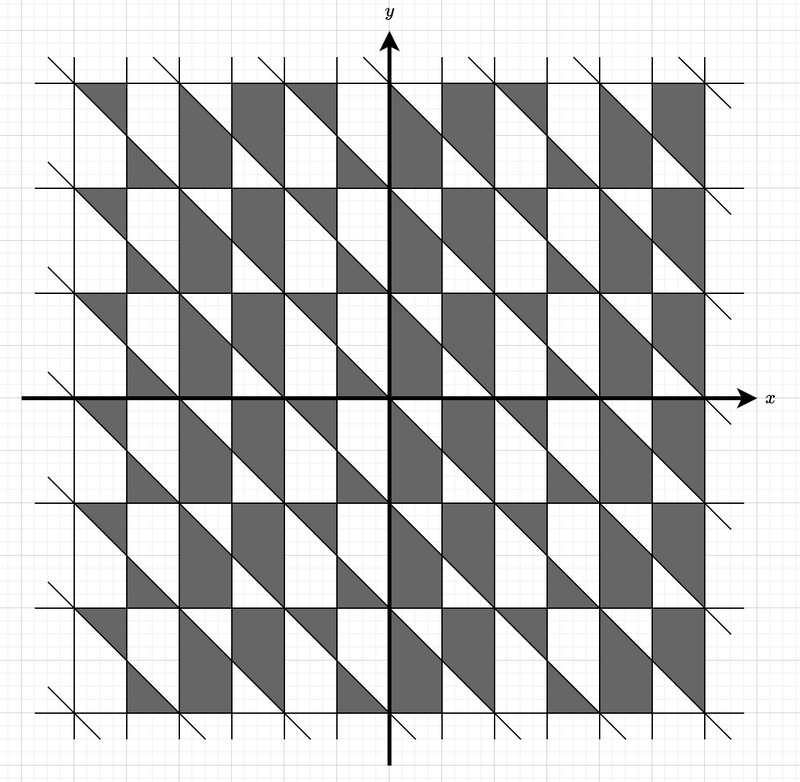
将 AtCoder 社的壁纸图案表示在 $xy$ 平面上，如下所示。 - 该平面被以下 $3$ 类直线分割： - $x = n$（$n$ 为整数） - $y = n$（$n$ 为偶数） - $x + y = n$（$n$ 为偶数） - 每个区域被涂成黑色或白色。任意一条直线相邻的两个区域颜色不同。 - 包含点 $(0.5, 0.5)$ 的区域被涂成黑色。 下图展示了该图案的一部分。  给定整数 $A, B, C, D$。考虑一个各边与 $x$、$y$ 轴平行、左下顶点为 $(A, B)$、右上顶点为 $(C, D)$ 的矩形。请计算该矩形内部被涂成黑色的区域的面积，并输出其 $2$ 倍的值。 可以证明，输出的值一定为整数。

输入从标准输入读入，格式如下： > $A$ $B$ $C$ $D$

请输出答案一行。

## 限制条件 - $-10^9 \leq A, B, C, D \leq 10^9$ - $A < C$ 且 $B < D$ - 输入均为整数 ## 样例解释 1 要求的是下图正方形包围的区域内被涂成黑色的区域面积。 该面积为 $5$，因此输出 $2$ 倍后的 $10$。 ## 样例解释 2 面积为 $5.5$，虽然是小数，但应输出的值为整数。 ## 样例解释 3 这是矩形取最大范围的情况，但输出仍在 64 位有符号整数范围内。 由 ChatGPT 4.1 翻译