AT_abc357_g [ABC357G] Stair-like Grid

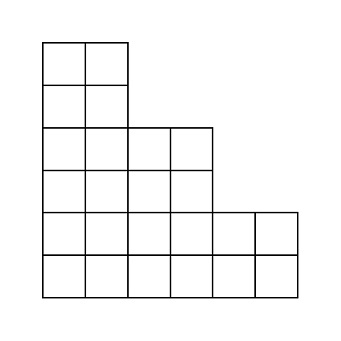
[problemUrl]: https://atcoder.jp/contests/abc357/tasks/abc357_g 縦 $ N $ 行の特殊な形をしたグリッドがあります。($ N $ は偶数) 上から $ i $ 行目にはマスが左端から $ \left\ \lceil\ \frac{i}{2}\ \right\ \rceil\ \times\ 2 $ マス並んでいます。 例えば $ N\ =\ 6 $ の時は下図のような形をしています。  上から $ i $ 行目、左から $ j $ 列目のマスを $ (i,\ j) $ と表します。 各マスは空きマスと壁マスのいずれかです。壁マスは $ M $ 個あり、$ i $ 個目の壁マスは $ (a_i,\ b_i) $ にあります。ただし $ (1,\ 1) $ と $ (N,\ N) $ は空きマスです。 $ (1,\ 1) $ を出発して、右または下に隣り合う空きマスへの移動を繰り返して $ (N,\ N) $ へ辿り着く方法は何通りありますか？答えを $ 998244353 $ で割った余りを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ $ \vdots $ $ a_M $ $ b_M $

$ (1,\ 1) $ を出発して、右または下に隣り合う空きマスへの移動を繰り返して $ (N,\ N) $ へ辿り着く方法の個数を $ 998244353 $ で割った余りを出力せよ。

### 制約 - $ 2\ \leq\ N\ \leq\ 2.5\ \times\ 10^5 $ - $ N $ は偶数 - $ 0\ \leq\ M\ \leq\ 50 $ - $ 1\ \leq\ a_i\ \leq\ N $ - $ 1\ \leq\ b_i\ \leq\ \left\ \lceil\ \frac{a_i}{2}\ \right\ \rceil\ \times\ 2 $ - $ (a_i,\ b_i)\ \neq\ (1,\ 1) $ かつ $ (a_i,\ b_i)\ \neq\ (N,\ N) $ - $ i\ \neq\ j $ ならば $ (a_i,\ b_i)\ \neq\ (a_j,\ b_j) $ - 入力される値は全て整数 ### Sample Explanation 1 問題文の条件を満たす経路は次の $ 2 $ 通りです。 - $ (1,\ 1)\ \to\ (1,\ 2)\ \to\ (2,\ 2)\ \to\ (3,\ 2)\ \to\ (3,\ 3)\ \to\ (3,\ 4)\ \to\ (4,\ 4) $ - $ (1,\ 1)\ \to\ (1,\ 2)\ \to\ (2,\ 2)\ \to\ (3,\ 2)\ \to\ (3,\ 3)\ \to\ (4,\ 3)\ \to\ (4,\ 4) $