AT_abc357_g [ABC357G] Stair-like Grid

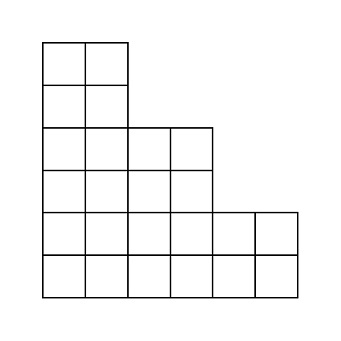
有一个特殊形状的纵向 $N$ 行的网格（$N$ 为偶数）。从上往下第 $i$ 行，从左端开始有 $\left\lceil \frac{i}{2} \right\rceil \times 2$ 个格子排列。 例如，当 $N=6$ 时，网格形状如下图所示。  从上往下第 $i$ 行、从左往右第 $j$ 列的格子记作 $(i, j)$。 每个格子要么是空格子，要么是墙格子。共有 $M$ 个墙格子，第 $i$ 个墙格子位于 $(a_i, b_i)$。但 $(1, 1)$ 和 $(N, N)$ 一定是空格子。 从 $(1, 1)$ 出发，每次只能移动到右边或下方相邻的空格子，问有多少种不同的路径可以到达 $(N, N)$？请将答案对 $998244353$ 取模后输出。

输入以如下格式从标准输入读入。 > $N$ $M$ $a_1$ $b_1$ $a_2$ $b_2$ $\vdots$ $a_M$ $b_M$

输出从 $(1, 1)$ 出发，每次只能移动到右边或下方相邻的空格子，最终到达 $(N, N)$ 的路径数，对 $998244353$ 取模后的结果。

## 限制条件 - $2 \leq N \leq 2.5 \times 10^5$ - $N$ 是偶数 - $0 \leq M \leq 50$ - $1 \leq a_i \leq N$ - $1 \leq b_i \leq \left\lceil \frac{a_i}{2} \right\rceil \times 2$ - $(a_i, b_i) \neq (1, 1)$ 且 $(a_i, b_i) \neq (N, N)$ - 若 $i \neq j$，则 $(a_i, b_i) \neq (a_j, b_j)$ - 所有输入均为整数 ## 样例解释 1 满足题目条件的路径有如下 $2$ 条： - $(1, 1) \to (1, 2) \to (2, 2) \to (3, 2) \to (3, 3) \to (3, 4) \to (4, 4)$ - $(1, 1) \to (1, 2) \to (2, 2) \to (3, 2) \to (3, 3) \to (4, 3) \to (4, 4)$ 由 ChatGPT 4.1 翻译